多変数関数における「方向微分」とは，ある方向のみを取り出した微分を指します。これについて，その定義と性質・求め方を詳しく解説しましょう。
方向微分の定義
定義（方向微分）
D\subset \mathbb{R}^n を n 次元領域とし， f\colon D\to \mathbb{R} を考える。
\boldsymbol{a}\in D,\; \boldsymbol{v}\in\mathbb{R}^n とし，さらに絶対値が十分小さい h\in \mathbb{R} に対し， \boldsymbol{a}+h\boldsymbol{v}\in D であるとき，
\color{red}\nabla_{\boldsymbol{v}}f(\boldsymbol{a})=\lim_{h\to 0} \frac{f(\boldsymbol{a}+h\boldsymbol{v})-f(\boldsymbol{a})}{h}
が存在するならば，これを， \boldsymbol{a} における \boldsymbol{v} 方向の方向微分 (directional derivative) といい，その値を方向微分係数という。方向微分は \color{red} \nabla_{\boldsymbol{v}}f の他， \color{red} \dfrac{\partial f}{\partial\boldsymbol{v}}(\boldsymbol{a}) などと書かれる。
多変数関数において，ある方向のみ取り出して，その曲線における微分を考えるという発想ですね。
なお， \boldsymbol{v} を単位ベクトルとすると，微分はその方向の接線の傾きに等しくなります。
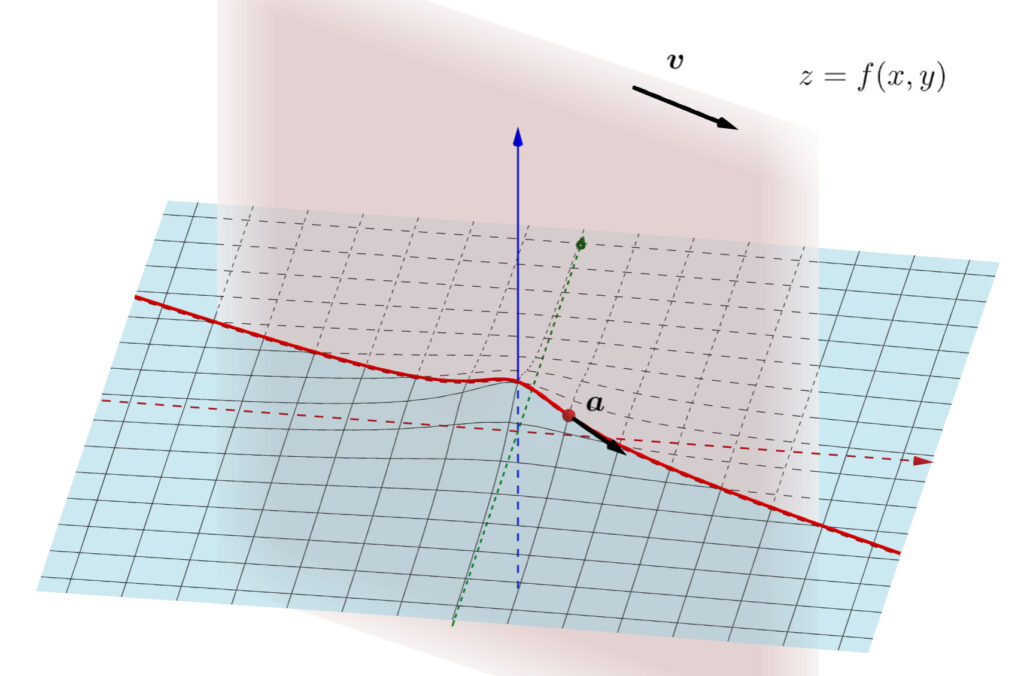
なお， x_j に関する偏微分は \boldsymbol{e_j}=(0,\dots, 0,1,0,\dots,0) ( j 成分のみ 1) 方向の方向微分といえます。この点で，偏微分は方向微分の一種です。
方向微分の性質～全微分との関係～
定理（全微分可能ならば任意の方向に方向微分可能）
D\subset \mathbb{R}^n を n 次元領域とし， f\colon D\to \mathbb{R} を考える。
f が \boldsymbol{a}\in D において全微分可能ならば，任意の方向に方向微分可能であり，
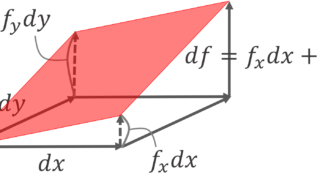
が成立する。ただし，\langle \cdot,\cdot \rangle は内積の意味であり，
は勾配 (gradient) を表す。
\boldsymbol{v}=(v_1,\dots, v_n) として，内積 \langle \nabla f(\boldsymbol{a}) , \boldsymbol{v}\rangle を書き下すことで，上の赤の式は
\color{red} \nabla_{\boldsymbol{v}} f(\boldsymbol{a}) = v_1\frac{\partial f}{\partial x_1}(\boldsymbol{a})+\dots + v_n\frac{\partial f}{\partial x_n}(\boldsymbol{a})
となりますね。
復習ですが，全微分可能であるとは，関数が一次近似できる，あるいは図形的に接平面が考えられるという具合の意味でした。一般に，全微分可能ならば偏微分可能であり，逆に偏微分可能で偏導関数が連続ならば全微分可能です。詳しくは以下で解説しています。
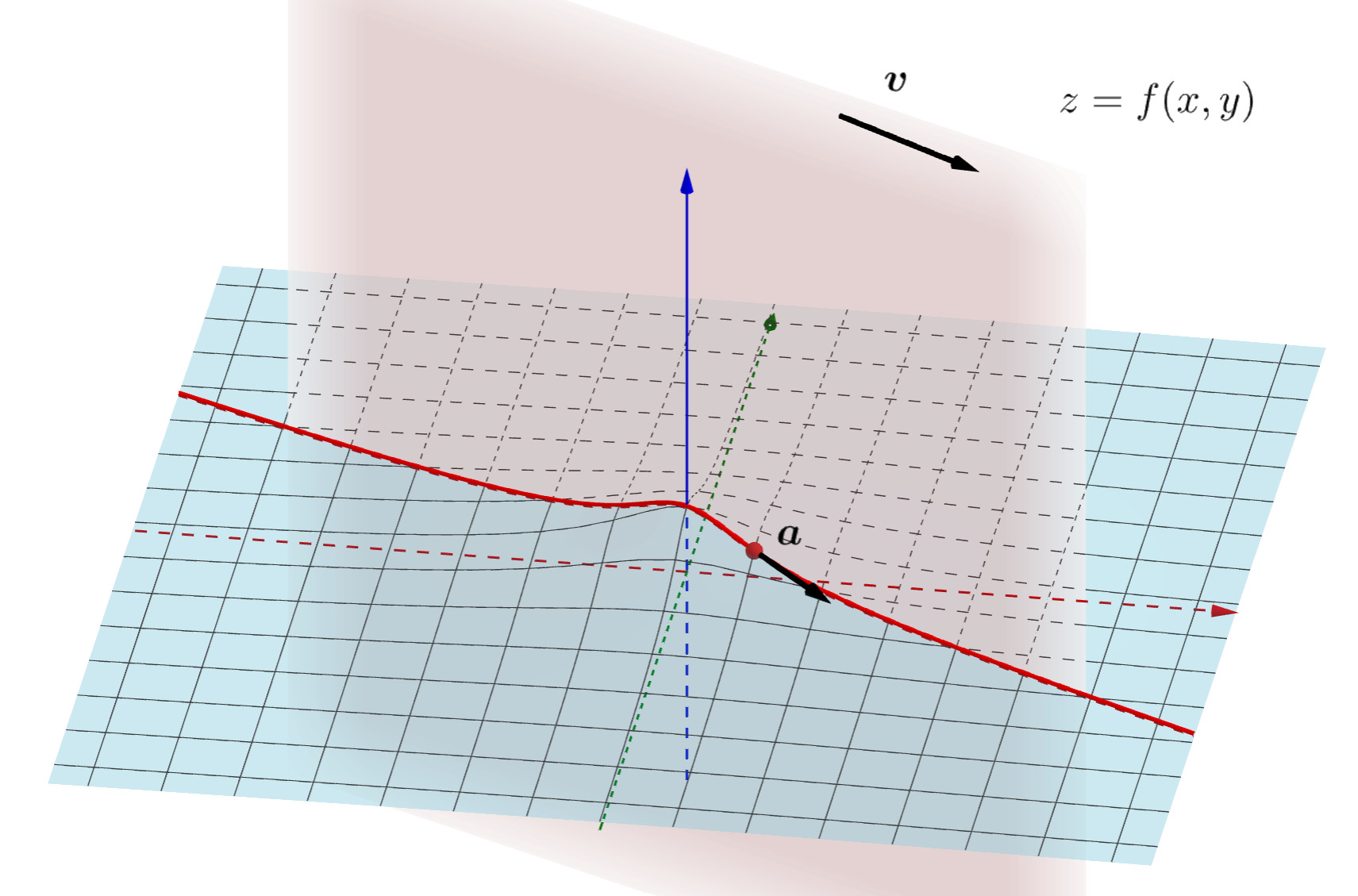
下の図は，n=2 の場合で，全微分可能なときに z=f(x,y) の接平面を考え， \boldsymbol{v} を単位ベクトルとすると，方向微分が接平面のその方向の傾きに等しいことを表現しています。
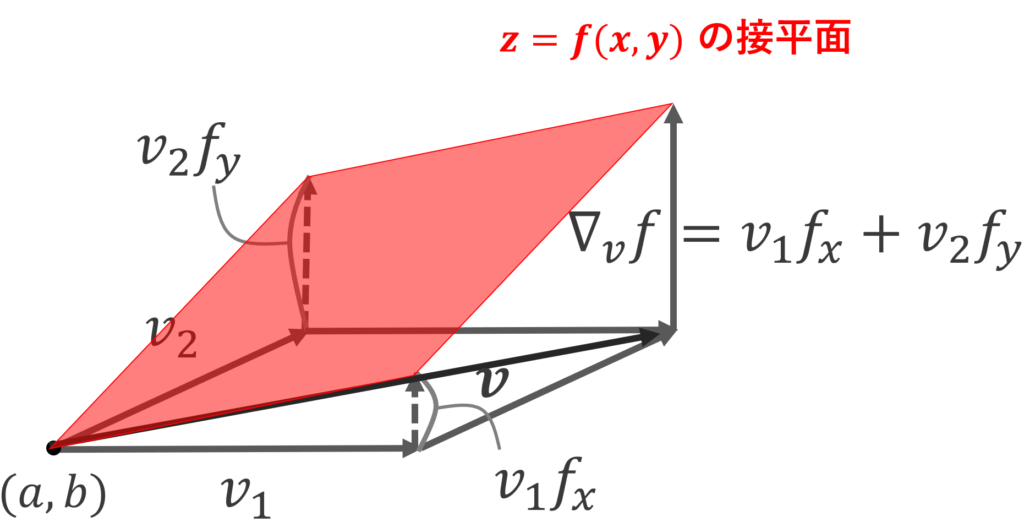
定理は，上の図のように，全微分可能ならばあらゆる方向の方向微分が可能で，それが偏微分の一次結合でかけると言っているんですね。
短いので簡単に証明しましょう。
証明
f は全微分可能より，
\begin{aligned}& \frac{f(\boldsymbol{a}+h\boldsymbol{v})-f(\boldsymbol{a})}{h} \\&= f_{x_1}(\boldsymbol{a})v_1+ \cdots+ f_{x_n}(\boldsymbol{a})v_n+\frac{o(h)}{h} \\ &\xrightarrow{h\to 0} f_{x_1}(\boldsymbol{a})v_1+ \cdots+ f_{x_n}(\boldsymbol{a})v_n\end{aligned}
となって，結論を得る。ここで，ランダウの記号 o を用いた。
証明終
方向微分の具体例
具体例を確認していきましょう。
例題1(全微分可能な例).
f(x,y)=x^2-y^2+xy の点 (x,y) における (x_0, y_0) 方向の方向微分を求めよ。
直接 \displaystyle \lim_{h\to 0}\frac{f(x+hx_0, y+hy_0)-f(x,y)}{h} を計算してもよいですが，上の定理を用いましょう。
解答
f_x(x,y)= 2x+y,\; f_y(x,y)=x-2y であり，これらは連続なので全微分可能である。従って，定理から
\begin{aligned}\nabla_{(x_0,y_0)}f(x,y) &=f_x(x,y)x_0+f_y(x,y)y_0 \\ &= (2x+y)x_0 + (x-2y)y_0. \end{aligned}簡単に求められましたね。
例題2(任意の方向微分可能だが全微分不可能な例).
f(x,y) = \begin{cases} x & y=0, \\ y & x=0, \\ 0 & xy\ne 0 \end{cases} の，原点における方向微分を求めよ。
直接計算してみましょう。
解答
(x_0,y_0) 方向の微分を考える。
\frac{f(hx_0,hy_0)-f(0,0)}{h} = \begin{dcases} x_0 & y_0=0, \\ y_0&x_0=0, \\0 &x_0y_0\ne 0\end{dcases}
であるから，両辺 h\to 0 として，
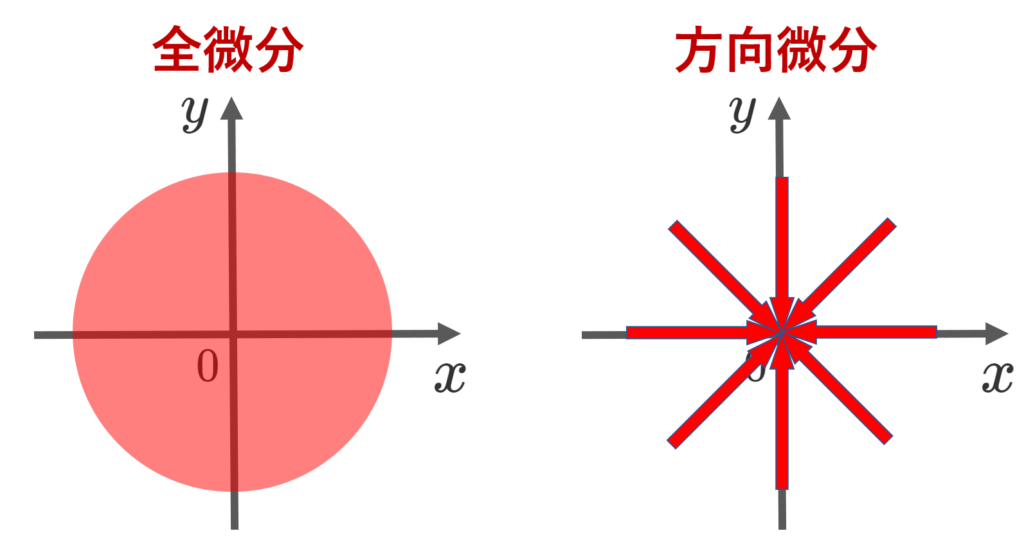
このとき，上の定理 \nabla_{\boldsymbol{v}} f(\boldsymbol{a})=\langle \nabla f(\boldsymbol{a}) , \boldsymbol{v}\rangle が成立していませんから，この関数が全微分不可能であることが分かります。このように，方向微分を考えることで，全微分不可能であることを判定することも可能です。
この関数は，全方向微分可能ですが全微分不可能な例になっています。
