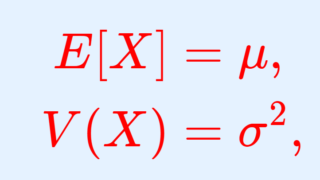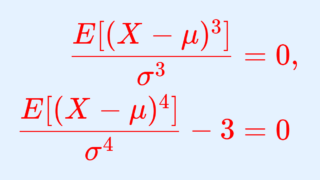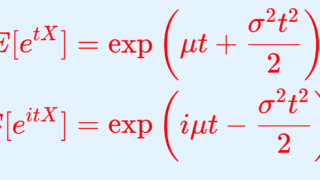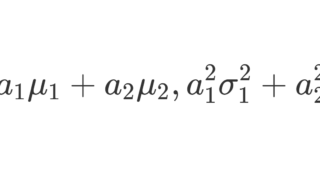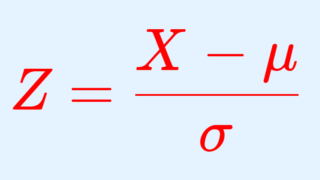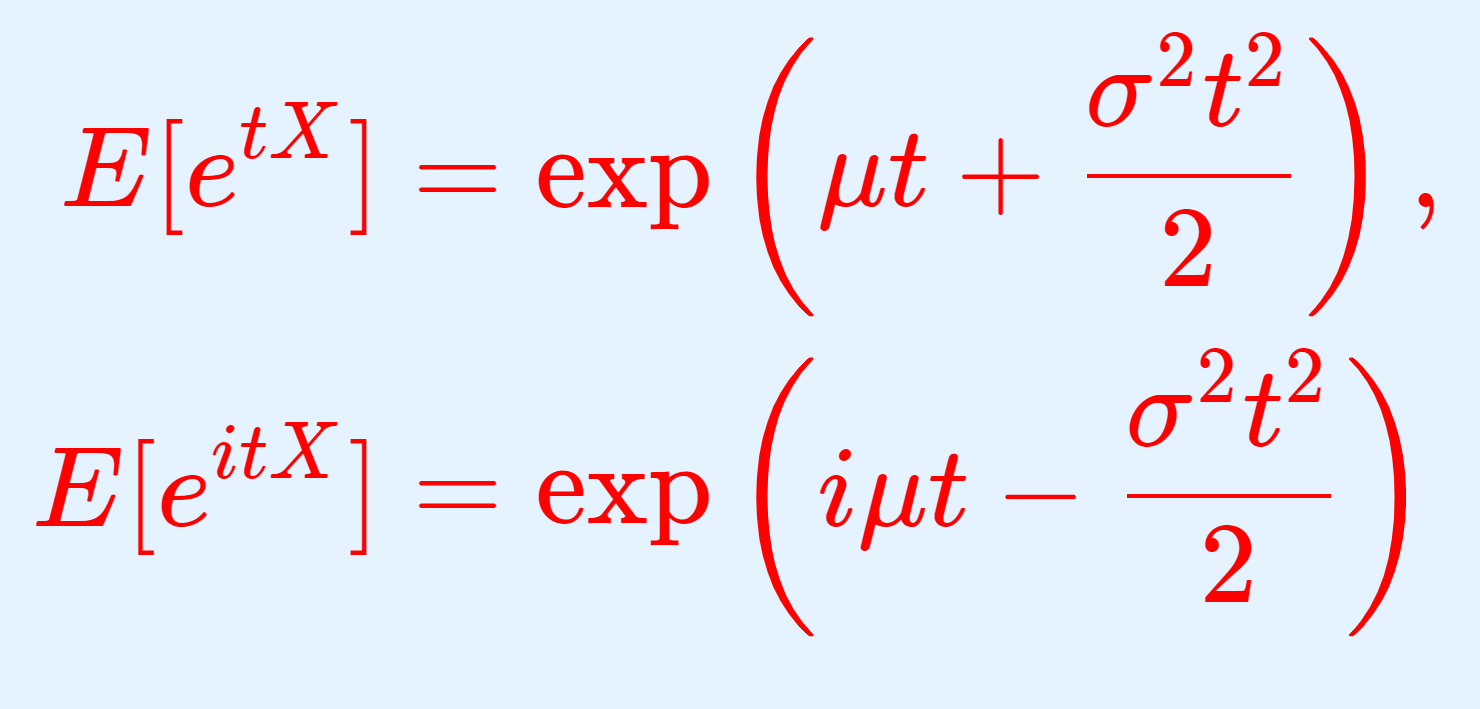正規分布(またはガウス分布)は,確率論や統計学において,最も基本的な連続型の分布だといえます。この分布について,定義と性質を分かりやすくまとめることにしましょう。
正規分布の定義
定義(正規分布)
X を確率変数, \mu\in \mathbb{R},\; \sigma > 0 とする。 X の確率密度関数が
\color{red} p(x) = \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}
となるとき, X は平均 \mu ,分散 \sigma^2 の正規分布 (normal distribution) に従うといい, \color{red} X\sim N(\mu, \sigma^2) とかく。
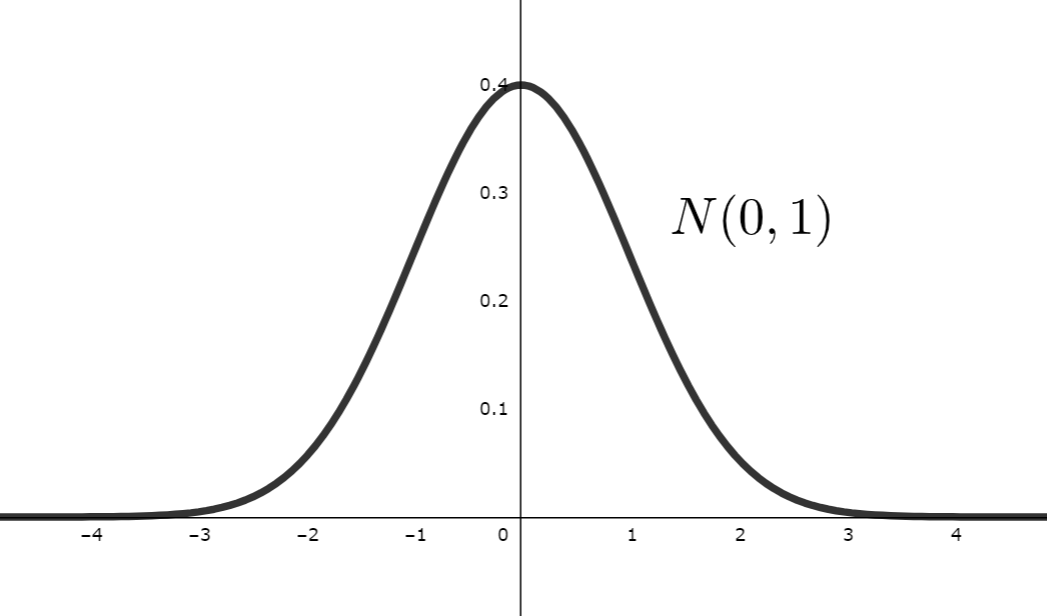
特に, \mu=0, \sigma^2=1 となる N(0,1) を標準正規分布 (standard normal distribution) という。
正規分布は,別名ガウス分布 (Gaussian distribution) とも言われます。
確率密度関数が p(x) とは, P(X\in A) = \int_A p(x)\, dx になるということですね。特に今の場合,
\begin{aligned}&P(X\in (-\infty, \infty)) \\&= \frac{1}{\sqrt{2\pi\sigma^2}}\int_{-\infty}^\infty e^{-\frac{(x-\mu)^2}{2\sigma^2}} \, dx = 1 \end{aligned}
となることは,「ガウス積分」によって確認できます(→ガウス積分のさまざまな形とその証明5つ)。
なお,確率密度関数は,指数部分がややこしいため, \displaystyle p(x)= \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left({-\frac{(x-\mu)^2}{2\sigma^2}} \right) とかくことも多いです。
標準正規分布の確率密度関数は,以下のような形になります(釣鐘型といわれます)。
平均 0 を中心に,左右対称になっているのが分かりますね。
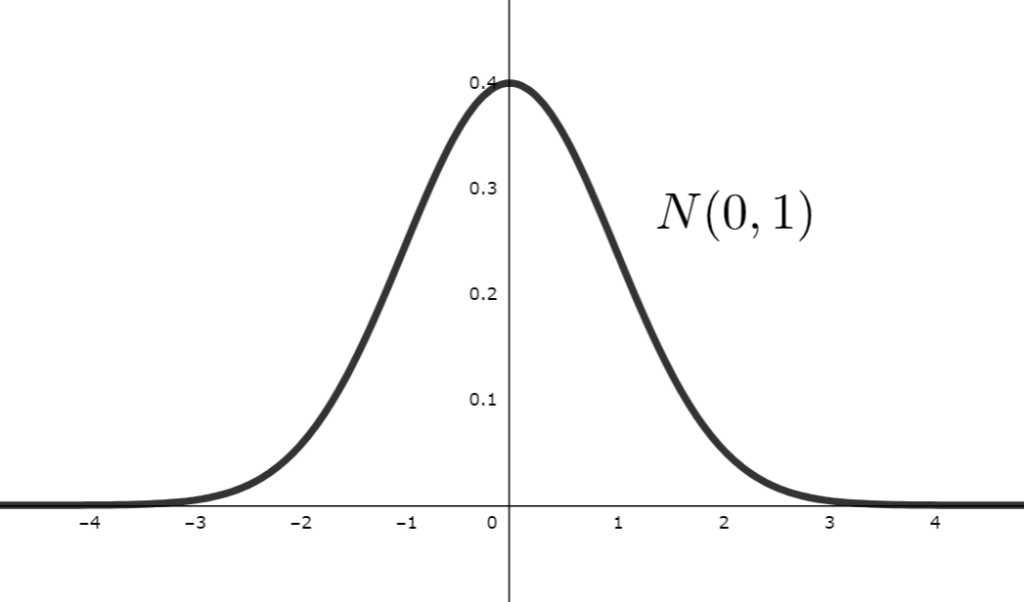
また,上の状態から,平均は \mu=0 のままで, \sigma の値を変えると,以下のように変化します。
\sigma が大きくなればなるほど,裾が広くなり,小さければ小さいほど,尖った形になるんですね。
正規分布の性質まとめ
正規分布は重要な性質がたくさんあります。まずは,それらを列挙しましょう。一般の正規分布 N(\mu,\sigma^2) と標準正規分布 N(0,1) それぞれについて,述べてみることにします。
| 正規分布 N(\mu, \sigma^2) | 標準正規分布 N(0,1) | |
|---|---|---|
| 確率 P(X\in A) | \small \displaystyle \dfrac{1}{\sqrt{2\pi\sigma^2}}\int_A e^{-\frac{(x-\mu)^2}{2\sigma^2}}\, dx | \small \displaystyle \dfrac{1}{\sqrt{2\pi}}\int_A e^{-\frac{x^2}{2}}\, dx |
| 確率の型 | 連続型 | 連続型 |
| 確率密度関数 p(x) | \small\displaystyle \dfrac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}} | \small\displaystyle \frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}} |
| 累積分布関数 F(x) = P(X\le x) | \small \displaystyle \frac{1}{2}\left[1+\operatorname{erf}\left( \frac{x-\mu}{\sqrt{2\sigma^2}}\right)\right] | \small \displaystyle \frac{1}{2}\left[1+\operatorname{erf} \left(\frac{x}{\sqrt{2}}\right)\right] |
| 期待値(平均) E[X] | \mu | 0 |
| 分散 V(X) | \sigma^2 | 1 |
| 標準偏差 \sqrt{V(X)} | \sigma | 1 |
| 歪度 \small \dfrac{E[(X-\mu)^3]}{\sigma^3} | 0 | 0 |
| 尖度 \dfrac{E[(X-\mu)^4]}{\sigma^4} -3 | 0 | 0 |
| 積率母関数(モーメント母関数) E[e^{tX}] | \displaystyle \exp \left( \mu t + \frac{\sigma^2 t^2}{2} \right) | \displaystyle e^{t^2/2} |
| 特性関数 E[e^{itX}] | \displaystyle \exp \left(i \mu t - \frac{\sigma^2 t^2}{2} \right) | \displaystyle e^{-t^2/2} |
| 再生性 | \scriptsize \begin{aligned}&X_1 \sim N(\mu_1, \sigma^2_1) ,\, X_2 \sim N(\mu_2, \sigma^2_2) \\ & \implies a_1X_1+a_2X_2 \sim N(a_1\mu_1+a_2\mu_2, a_1^2\sigma_1^2+a_2^2\sigma_2^2)\end{aligned} |
| 標準化 | \small X\sim N(\mu, \sigma^2) \implies \dfrac{X-\mu}{\sigma}\sim N(0,1) |
| 中心極限定理 (X_k) \text{ : iid} | \frac{X_1+\cdots+ X_n-n\mu}{\sqrt{n}\sigma} \xrightarrow{n\to\infty} N(0,1) |
累積分布関数以降について,一つずつ確認していきます。
正規分布の累積分布関数(分布関数)
定理(正規分布の累積分布関数(分布関数))
X\sim N(\mu, \sigma^2) とするとき, X の累積分布関数(分布関数)は,
\color{red} \begin{aligned}F(x) &= P(X\le x) \\ &= \frac{1}{\sqrt{2\pi\sigma^2}}\int_{-\infty}^x e^{-\frac{(t-\mu)^2}{2\sigma^2}} \, dt \\ &=\frac{1}{2}\left[1+\operatorname{erf}\left( \frac{x-\mu}{\sqrt{2\sigma^2}}\right)\right]\end{aligned}
である。ただし,\displaystyle \operatorname{erf}(x) = \frac{2}{\sqrt{\pi}}\int_0^x e^{-t^2}\, dt (誤差関数, error function)である。
累積分布関数の最後の等式は,正規分布の対称性と置換積分により,
\begin{aligned}& \frac{1}{\sqrt{2\pi\sigma^2}}\int_{-\infty}^x e^{-\frac{(t-\mu)^2}{2\sigma^2}} \, dt \\ &= \frac{1}{2}+\frac{1}{\sqrt{2\pi\sigma^2}} \int_{\mu}^xe^{-\frac{(t-\mu)^2}{2\sigma^2}} \, dt \\ &= \frac{1}{2} + \frac{1}{\sqrt{\pi}}\int_0^{\frac{x-\mu}{\sqrt{2\sigma^2}}} e^{-s^2}\, ds \\ &= \frac{1}{2}\left[1+\operatorname{erf}\left( \frac{x-\mu}{\sqrt{2\sigma^2}}\right)\right] \end{aligned}
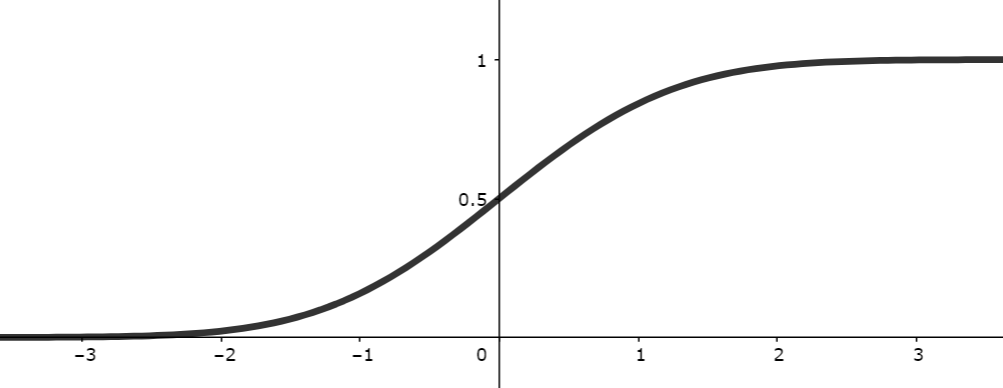
であることから分かります。標準正規分布 N(0,1) の累積分布関数をグラフで描くと,以下のようになります。
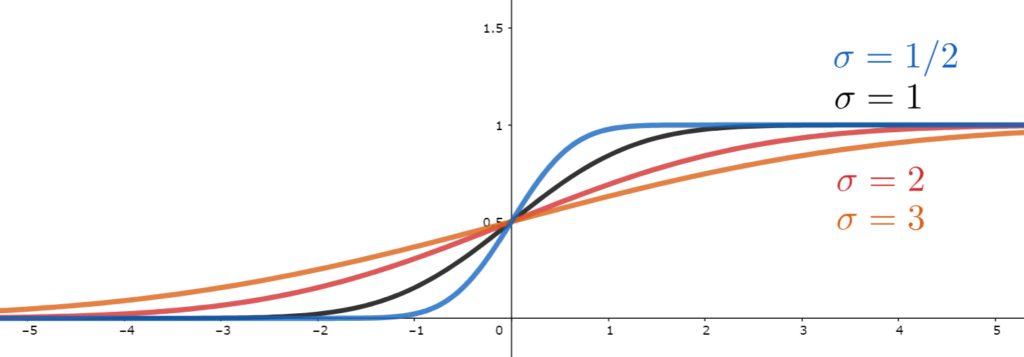
平均は \mu=0 のままで, \sigma の値を変えると,以下のように変化します。
正規分布の期待値(平均)・分散・標準偏差
定理(正規分布の期待値(平均)・分散・標準偏差)
X\sim N(\mu,\sigma^2 ) とする。このとき, X の期待値(平均)・分散・標準偏差はそれぞれ
\color{red} \begin{aligned} E[X]&= \mu, \\ V(X)&= \sigma^2, \\ \sqrt{V(X)} &= \sigma \end{aligned}
である。
N(\mu, \sigma^2) という表記は,平均と分散を並べて書いたものになります。
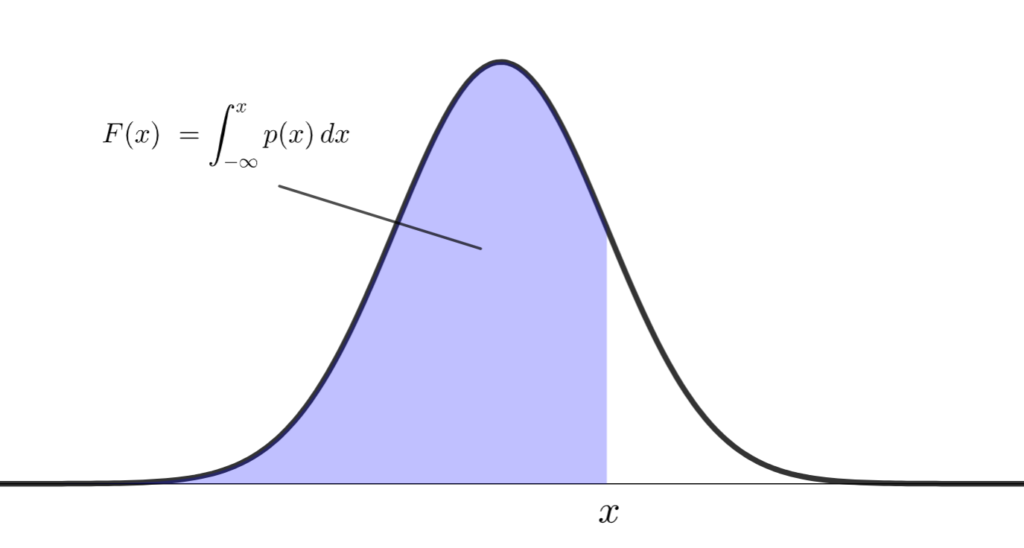
なお,標準偏差と正規分布のグラフの関係は,下図のようになります。
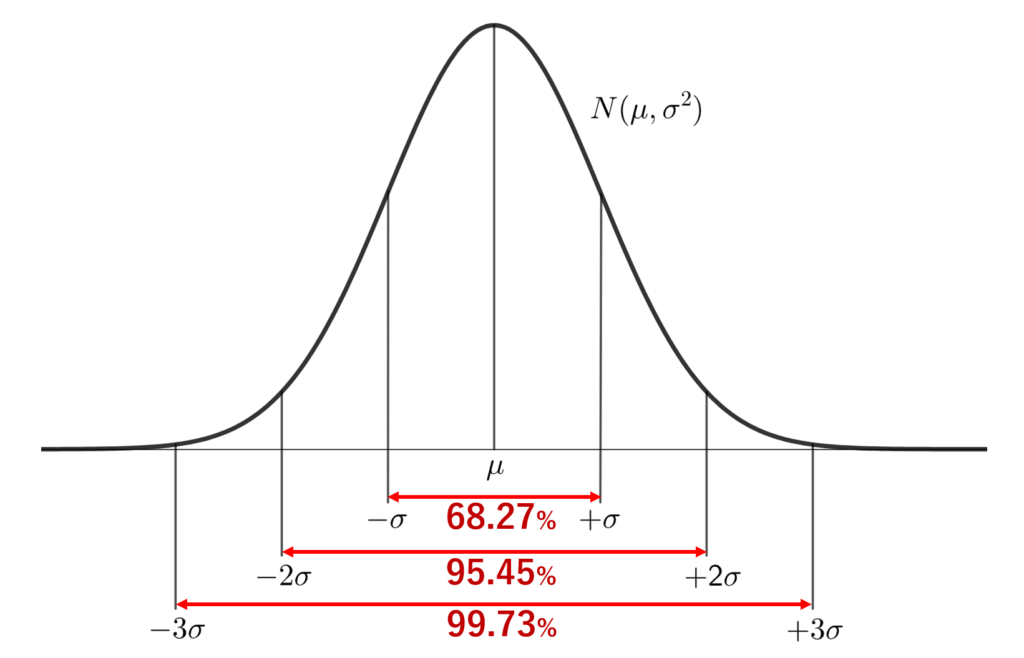
\pm\sigma 点は,ちょうど変曲点になっています。
また,ちょうど 95\% になるのは \pm 1.96\sigma, 99\% になるのは \pm 2.58\sigma のところです。
正規分布の期待値・分散・標準偏差の証明については,以下の記事を参照してください。
正規分布の歪度・尖度
定理(正規分布の歪度・尖度)
X\sim N(\mu,\sigma^2 ) とする。このとき, X の歪度・尖度はそれぞれ
\color{red} \begin{aligned} \dfrac{E[(X-\mu)^3]}{\sigma^3}&= 0, \\ \dfrac{E[(X-\mu)^4]}{\sigma^4} -3&= 0 \\ \end{aligned}
である。
歪度(わいど)とは,分布がどれだけ非対称で歪んで(ゆがんで)いるかを表す指標で,尖度(せんど)とは,「正規分布と比べて」分布がどれだけ尖って(とがって)いるかを表す指標です。正規分布は,ちょうどどちらも 0 になります。
証明については,以下の記事を参照してください。
正規分布の積率母関数(モーメント母関数)・特性関数
定理(正規分布の積率母関数(モーメント母関数)・特性関数)
X\sim N(\mu,\sigma^2 ) とする。このとき, X の積率母関数(モーメント母関数)・特性関数はそれぞれ
\color{red} \begin{aligned} E[e^{tX}]&= \exp \left( \mu t + \frac{\sigma^2 t^2}{2} \right) , \\ E[e^{itX}]&= \exp \left( i\mu t - \frac{\sigma^2 t^2}{2} \right) \\ \end{aligned}
である。
正規分布は,その積率母関数(モーメント母関数)・特性関数もよく使われますね。これは,以下の記事で証明しています。
正規分布の再生性
定理(正規分布の再生性)
\mu_1, \mu_2 \in \mathbb{R},\; \sigma_1,\sigma_2>0 とする。 X_1 \sim N(\mu_1, \sigma_1^2),\; X_2\sim N(\mu_2, \sigma_2^2) を独立とすると, a_1, a_2\in \mathbb{R} に対し,
\small\color{red} a_1X_1+a_2X_2\sim N(a_1\mu_1+a_2\mu_2, a_1^2\sigma_1^2+a_2^2\sigma_2^2)
である。特に,正規分布の和や定数倍は,また正規分布になる。
同じ分布族の独立な確率変数を2つ足すと,また同じ分布族に属するとき,これを分布の再生性 (reproductive property) といいます。正規分布やポアソン分布は,再生性をもつ分布として有名です。
これの証明については,以下の記事を参照してください。
正規分布の標準化
定理(正規分布の標準化)
X\sim N(\mu, \sigma^2) とするとき,
\color{red} Z = \frac{X-\mu}{\sigma}
とすると, Z\sim N(0,1) になる。
正規分布の標準化 (standardization)とは, N(\mu,\sigma^2) に従う確率変数を,変換によって N(0,1) に従うようにすることです。
これについては, X-\mu \sim N(0, \sigma^2) であることと,上の再生性の話からも分かりますが,以下の記事でも解説しています。
中心極限定理と正規分布
中心極限定理は,非常に強力で,分布の近似に使われる有名な定理です。正規分布が大切なのは,この定理のおかげと言ってもいいでしょう。主張を述べます。
定理(中心極限定理)
(X_k) を平均 \mu ,分散 \sigma^2 が有限値である,独立同分布な確率変数列とする。このとき, S_n=\sum_{k=1}^n X_k とおくと,
\color{red} \frac{S_n-n\mu}{\sqrt{n}\sigma}
は n\to\infty で標準正規分布 N(0,1) に分布収束する。すなわち, \alpha \in \mathbb{R} に対して,
となる。
ここでポイントなのは, (X_k ) は平均・分散をもつ独立同分布であれば,どんな分布でも良いということです。どんな分布であっても,その十分多くの和は正規分布で近似できるということは,かなり強力な定理と言えるでしょう。
この意味で,正規分布は最も基本的かつ強力な分布だといえます。実際,統計学においては,多くの分布を正規分布で近似します。