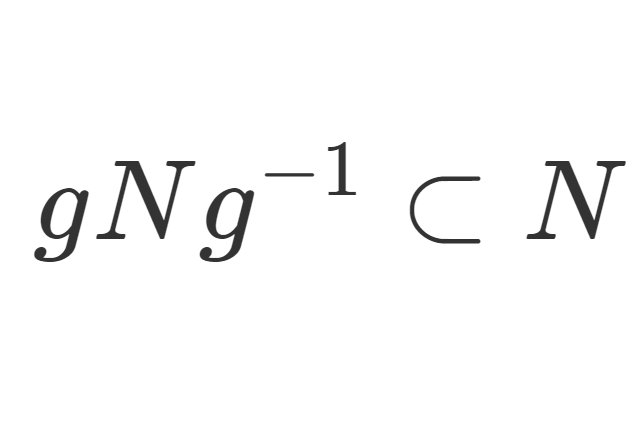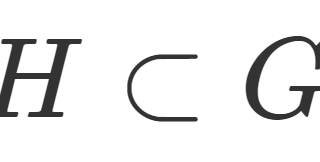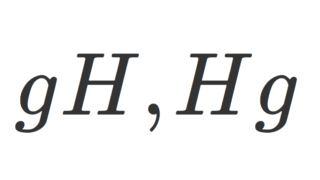正規部分群とは, gNg^{-1}\subset N が成立する部分群 N\subset G のことを言います。
正規部分群の定義と準同型写像の核を用いた判定方法,具体例と大事な性質まで紹介します。
正規部分群とは
定義(正規部分群)
G を群,N\subset G を部分群とする。N が正規部分群 (normal subgroup) とは,任意の g\in G に対して
\Large\color{red}gNg^{-1}\subset N
が成り立つことをいう。ただし, gNg^{-1}=\{gng^{-1}\mid n\in N\} とした。 N が G の正規部分群であることを \color{red} N\triangleleft G とかく。
定義を言い換えると,任意の g\in G,\, n\in N に関して gng^{-1}\in N となります。
n\mapsto gng^{-1} のような変換を「共役変換」や「相似変換」や「内部自己同型」と言ったりしますが,共役変換しても不変な部分群というわけですね。
なお,正規部分群の定義は \color{red} gNg^{-1} =N としても同じです。実際,任意の g\in G について gNg^{-1}\subset N の左から g^{-1},右から g をかけることで N\subset g^{-1}Ng が言えるので, g を g^{-1} と思い直せば N\subset gNg^{-1} も従いますね。
正規部分群の基本的な判定方法
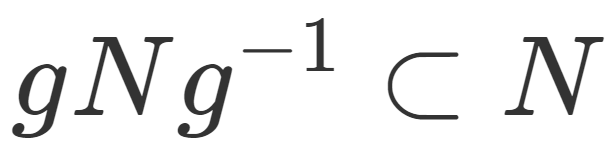
正規部分群を判定するにあたって,以下の定理は最も基本的です。
定理( \operatorname{Ker} f は正規部分群)
G_1, G_2 を群,f\colon G_1\to G_2 を準同型とする。このとき,
\color{red}\operatorname{Ker} f=\{ g\in G_1\mid f(g) = e_{G_2}\}
は G_1 の正規部分群である。ただし, e_{G_2} は G_2 の単位元を表す。
準同型写像の核 (kernel) は正規部分群というわけですね。正規部分群であることの最も基本的な判定方法といえるでしょう。
証明
N= \operatorname{Ker} f とする。まず N\subset G_1 が部分群であることを示す。
f(e_{G_1})=e_{G_2} より e_{G_1}\in N である。 a,b\in N とすると, f(ab) =f(a)f(b)=e_{G_2}e_{G_2}=e_{G_2} より, ab\in N である。さらに f(a^{-1})=f(a)^{-1} = e_{G_2}^{-1} = e_{G_2} より a^{-1}\in N である。したがって,部分群の定義と判定方法~例4つと性質~により, N\subset G_1 は部分群である。
つづいて, n\in N,\; g\in G_1 を任意にとる。このとき,
\!\! \begin{aligned} f(gng^{-1}) &= f(g)f(n)f(g)^{-1} = f(g)e_{G_2}f(g)^{-1} \\ &= f(g)f(g)^{-1} = e_{G_2}\end{aligned}
なので, gng^{-1}\in N となるから, N は正規部分群である。
証明終
これを踏まえて,具体例を確認しましょう。
正規部分群の例とそうでない例
例1(自明な部分群).
G を群としたとき, G そのものや単位元のみの集合 \{e\} は正規部分群である。これを自明な正規部分群という。
これは明らかでしょう。
例2(可換群(アーベル群)).
G を可換群(アーベル群)としたとき,任意の部分群 N\subset G は正規部分群である。
可換であれば, gNg^{-1} = gg^{-1}N = N のように交換してもよいので,任意の部分群が正規部分群になります。
交代群 A_3 が正規部分群であることは,置換の符号を返す準同型 \operatorname{sgn}\colon S_3 \to\{\pm 1\} に対して, A_3 = \operatorname{Ker} (\operatorname{sgn} ) となっているからです。より一般に, A_n\subset S_n は正規部分群です。
一方で, (13)(12)(13)^{-1} =(23) \notin H より, H\subset S_3 は正規部分群ではありませんね。
関連記事:【置換群】対称群・交代群の定義と性質
例4(行列群(一般線形群)).
2 次正則行列(可逆行列)全体の集合のなす一般線形群 \mathrm{GL}_2(\mathbb{R}) において,その特殊線形群
\mathrm{SL}_2(\mathbb{R})=\{ A\in\mathrm{GL}_2(\mathbb{R})\mid \det A = 1\}
は \mathrm{GL}_2(\mathbb{R}) の正規部分群である。一方で
は \mathrm{GL}_2(\mathbb{R}) の部分群であるが,正規部分群ではない。
\mathrm{SL}_2(\mathbb{R}) が正規部分群であることは,準同型写像 \det \colon \mathrm{GL}_2(\mathbb{R})\to \mathbb{R}\setminus \{0\} において, \mathrm{SL}_2(\mathbb{R})=\operatorname{Ker}(\det) であるからです。同様に 2 を n にした \mathrm{SL}_n( \mathbb{R})\subset \mathrm{GL}_n(\mathbb{R}) も正規部分群です。一方で,
\begin{aligned} &\begin{pmatrix} 1&1 \\1& 0\end{pmatrix} \begin{pmatrix} 0&1 \\1& 0\end{pmatrix} \begin{pmatrix} 1&1 \\1& 0\end{pmatrix}^{-1} \\ &= \begin{pmatrix} 1&1 \\1& 0\end{pmatrix} \begin{pmatrix} 0&1 \\1& 0\end{pmatrix} \begin{pmatrix}0&1 \\1& -1 \end{pmatrix} \\ &= \begin{pmatrix} 1&0 \\1& -1 \end{pmatrix}\notin H \end{aligned}
より,上で定義した H 正規部分群ではありません。
正規部分群の性質
正規部分群の大事な性質を挙げましょう。
正規部分群の共通部分も正規部分群
定理(正規部分群の共通部分)
N_1,N_2\subset G を共に正規部分群としたとき,N_1\cap N_2 も正規部分群である。
証明
N_1\cap N_2 が部分群であることは容易なので省略する。 n\in N_1\cap N_2 と g\in G を任意に取る。
N_1 は正規部分群なので, gng^{-1}\in N_1 であり,同様に gng^{-1}\in N_2 である。よって gng^{-1}\in N_1\cap N_2 なので, N_1\cap N_2 は正規部分群である。
証明終
同様に, \{N_{\lambda}\}_{\lambda\in \Lambda} を正規部分群の族としたとき, \bigcap_{\lambda\in\Lambda} N_{\lambda} も正規部分群になります。
正規部分群は左剰余類と右剰余類が一致
定理(正規部分群 \iff 左剰余類と右剰余類が一致)
N\subset G を部分群とするとき,以下の2つは同値である。
- N が正規部分群である。
- 任意の g\in G に対して, \color{red}gN = Ng が成立する。すなわち左剰余類と右剰余類が一致する。
正規部分群は,左剰余類と右剰余類が一致する群だということですね。この考え方は非常に重要です。
gN=Ng とは, gN\subset Ng かつ Ng \subset gN のことです。
gN\subset Ng とは,任意の n\in N に対して,ある n'\in N が存在して, gn=n'g 成り立つことで, Ng\subset gN とは,任意の n\in N に対して,ある n'\in N が存在して, ng =gn' 成り立つことを言います。
証明
1. \implies 2.について
n\in N,\; g\in G を任意に取る。
N は正規部分群なので gng^{-1}\in N である。特にある n'\in N が存在して, gng^{-1}=n' である。右から g をかけて gn=n'g となるから, gN\subset Ng である。
g を g^{-1} に置き換えて同様に考え,左から g をかけることで Ng\subset gN もわかる。
2. \implies 1.について
n\in N,\; g\in G を任意に取る。
gn \in gN =Ng より,ある n' が存在して gn=n'g となる。両辺右から g^{-1} をかけて gng^{-1}=n'\in N より, N は正規部分群である。
証明終