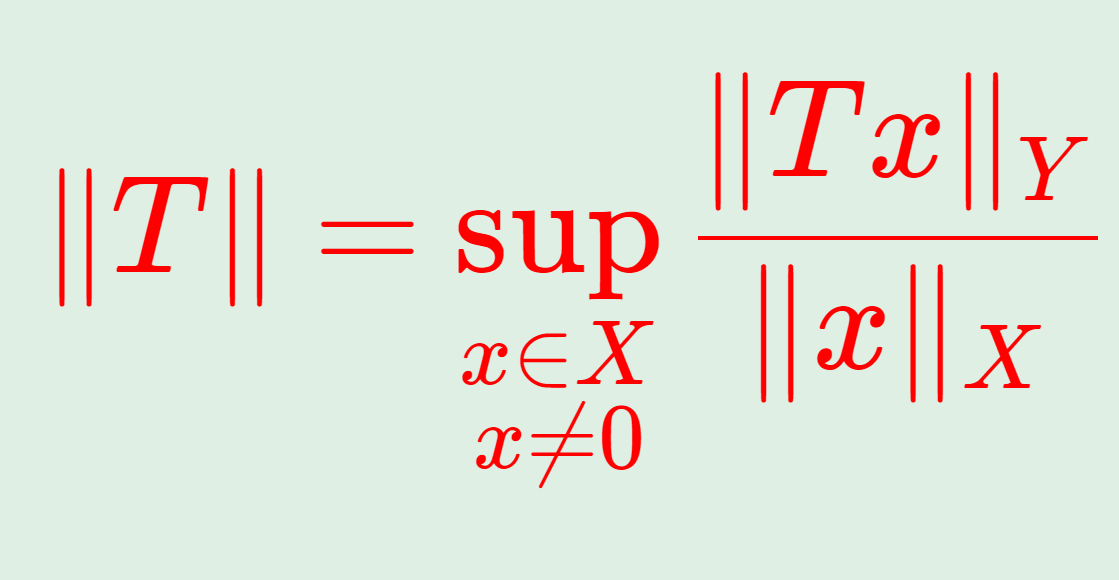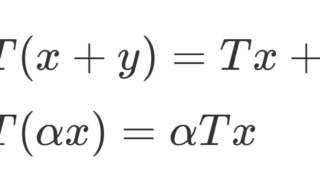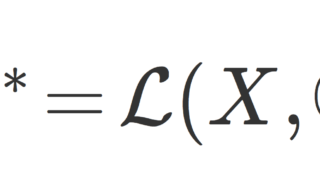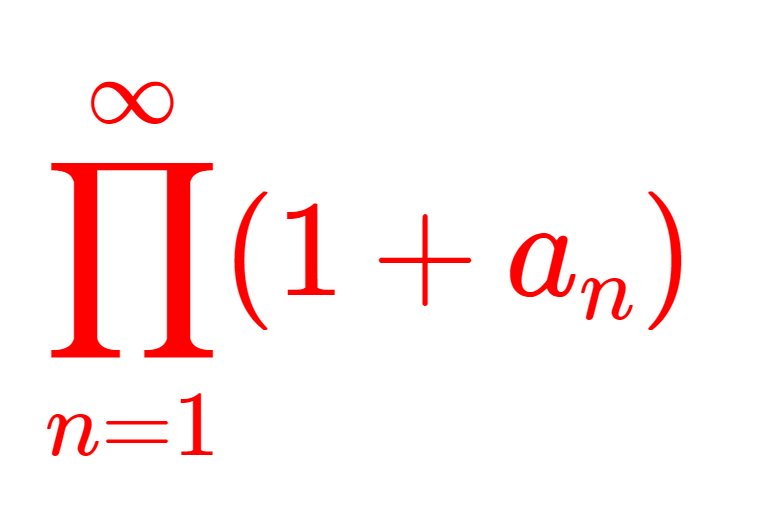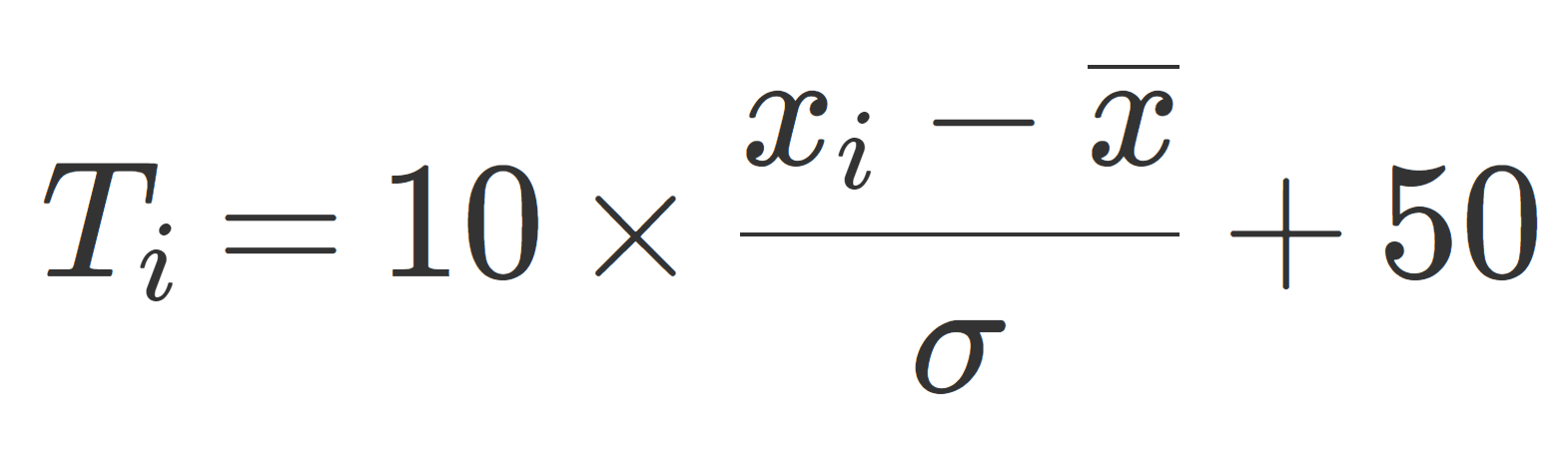作用素ノルムとは～定義と具体例と性質～

有界線形作用素 $T\colon X\to Y$ に対して，そのノルムは

\|T\| = \sup_{x\ne 0} \frac{\|Tx\|_Y}{\|x\|_X} =\sup_{\|x\|_X=1} \|Tx\|_Y

と定義されます。作用素ノルムとは，作用素同士の「距離」を定めるものです。これにより，作用素の扱える範囲が広がるわけです。

作用素ノルムについて，その定義と，作用素ノルムが「ノルム」になっていることの証明，具体例や性質を紹介します。

作用素ノルムの定義とノルムである証明
1. 作用素ノルムの定義
2. 作用素ノルムがノルムであること
作用素ノルムの具体例
作用素ノルムその他の性質
1. 作用素の合成とノルム
2. 作用素の空間の完備性
関連する記事

作用素ノルムの定義とノルムである証明

2つのノルム空間 $(X,\|\cdot\|_X), (Y, \|\cdot \|_Y)$ に対し，線形作用素 $T\colon X\to Y$ が有界 (bounded) であるとは，

$D(T)=X$ ( $T$ の定義域が $X$ )
$\|Tx\|_Y\le M\|x\|_X \; (x\in X)$ となる $M>0$ が存在

という2つが成り立つことを言うのでした(→線形作用素とその有界性について詳しく)。特に2つ目より，

\sup_{\substack{x\in X \\ x\ne 0}} \frac{\|Tx\|_Y}{\|x\|_X}\le M

となります。作用素ノルムは，有界線形作用素に対して，上式の左辺で定義されます。

作用素ノルムの定義

定義（作用素ノルム）

$X,Y$ をノルム空間とし， $T\colon X\to Y$ を有界線形作用素とする。このとき，

\color{red}\large \| T\| = \sup_{\substack{x\in X \\ x\ne 0}} \frac{\|Tx\|_Y}{\|x\|_X}

を作用素ノルム (operator norm) という。

$X$ と $Y$ のノルムを区別して $\|\cdot\|_X,\|\cdot \|_Y$ などとかいたように，作用素ノルムは $\|\cdot\|_{\mathcal{L}(X,Y)}$ などとかかれることもあります。

定義の前にかいた議論より， $\|T\|<\infty$ です。ノルムの性質 $\|k x\| = |k|\|x\| \; (k\in \mathbb{C})$ を用いることで，

\begin{aligned} \| T\| &= \textcolor{red}{\sup_{x\ne 0} \frac{\|Tx\|_Y}{\|x\|_X}} \\ &= \sup_{x\ne 0} \left\|T\frac{x}{\|x\|_X}\right\|_Y \\ &= \textcolor{red}{\sup_{\|x\|_X=1} \|Tx\|_Y} \\ &= \textcolor{red}{\sup_{\|x\|_X \le 1} \|Tx\|_Y} \end{aligned}

となることが分かりますから，作用素ノルムは上の式のどれで定義しても構いません。また，定義の式より， $\|T\|\ge \frac{\|Tx\|_Y}{\|x\|_X} \; (x\ne 0)$ ですから，両辺 $\|x\|$ 倍して， $\color{red} \|Tx\|_Y \le \|T\|\|x\|_X\; (x\in X)$ も成り立ちます。

作用素「ノルム」といわれるのは，以下の性質があるからです。

作用素ノルムがノルムであること

定理1（作用素ノルムはノルムである）

$X,Y$ をノルム空間とし， $\large \color{red} \mathcal{L}(X,Y)$ を有界線形作用素 $T\colon X\to Y$ のなす空間とする( $\large \color{red} B(X,Y)$ とかくこともある)。これは，作用素ノルム

\large \| T\| = \sup_{\substack{x\in X \\ x\ne 0}} \frac{\|Tx\|_Y}{\|x\|_X}

により，ノルム空間となる。

この定理を証明しておきましょう。

証明

第一に $\mathcal{L}(X,Y)$ が(以下の2つの演算を定義することで)ベクトル空間になることを確認する。 $S,T\in \mathcal{L}(X,Y),\; k\in \mathbb{C}$ に対し，

$(S+T)x= Sx+Tx\quad (x\in X)$
$(kT)x= k(Tx) \quad (x\in X)$

と定義すると， $S+T, kT$ も定義域が $X$ の作用素である。また， $S,T\in \mathcal{L}(X,Y)$ より， $\|Sx\|_Y\le M\|x\|_X, \; \|Tx\|_Y\le N \|x\|_X\; (x\in X)$ となる $M,N>0$ が存在する。このとき， $x\in X$ に対し

$\|(S+T)x\|_Y = \|Sx+Tx\|_Y \le \|Sx\|_Y+\|Tx\|_Y\le (M+N)\|x\|_X$
$\|(kT)x\|_Y = \|k(Tx)\|_Y= |k|\|Tx\|_Y\le |k|N \|x\|_X$

が成立するため， $S+T\in \mathcal{L}(X,Y),\; kT\in\mathcal{L}(X,Y)$ となる。和と定数倍の演算がベクトル空間の定義をみたしていることはすぐにわかるので，示せた。

次に，ノルム空間であることを示す。

$\color{red}\|T\|\ge 0$ は明らか。

\begin{aligned} \|(S+T)x\|_Y &= \|Sx+Tx\|_Y\\& \le \|Sx\|_Y+\|Tx\|_Y\end{aligned}

である。両端辺に着目して，

\begin{aligned}&\sup_{\|x\|=1} \|(S+T)x\|_Y\\ &\le \sup_{\|x\|=1} (\|Sx\|_Y+\|Tx\|_Y) \\ &\le \sup_{\|x\|=1}\|Sx\|_Y+\sup_{\|x\|=1}\|Tx\|_Y \end{aligned}

なので， $\color{red}\|S+T\|\le \|S\|+\|T\|$ である。また，

\|(kT)x\|_Y = \|k(Tx)\|_Y= |k|\|Tx\|_Y

の両端辺で $\sup_{\|x\|=1}$ を取ると， $\color{red} \|kT\| = |k|\|T\|$ も成り立つ。

また， $T=0$ (零作用素)とすると， $\|T\|=0$ は明らかで，逆に $\|T\|=0$ とすると， $\|Tx\|_Y=0 \; (x\in X)$ となるから， $Y$ におけるノルムの定義より， $Tx=0\; (x\in X)$ がわかる。したがって， $T=0$ となる。ゆえに， $\color{red}T=0\iff \|T\|=0$ である。

以上，赤字の4式より， $\mathcal{L}(X,Y)$ がノルム空間であることが示された。

証明終

作用素ノルムの具体例

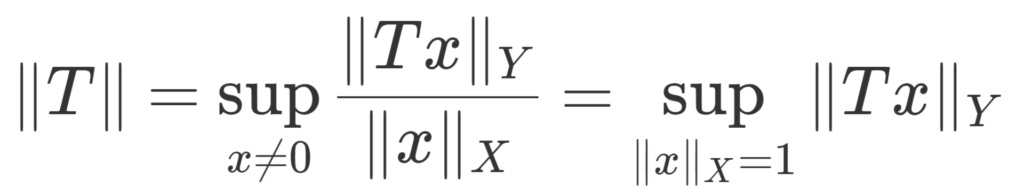
例1（数列空間）

$l^2$ を $\sum_{n=1}^\infty |a_n|^2<\infty$ となる複素数列 $(a_n)$ 全体のなすノルム空間(ヒルベルト空間)とする。ただし，ノルムは

\|(a_n)\| = \left(\sum_{n=1}^\infty |a_n|^2\right)^{1/2}

で定める。作用素 $S,T\colon l^2\to l^2$ を

\begin{aligned} S(a_1,a_2,a_3,\dots)&= (0,a_1,a_2,\dots)\\ T(a_1,a_2,a_3,\dots) &= (a_2,a_3,a_4,\dots) \end{aligned}

と定めると， $S,T$ は有界線形作用素で， $\|S\|=\|T\|=1$ である。

$S$ は右側にシフトする作用素で， $T$ は左側にシフトする作用素です。 $\|S\|=\|T\|=1$ になることを確認しましょう。

$a=(a_n) \in l^2$ に対し， $\|a\|=1$ とすると， $\|Sa\|=1$ ですから， $\|S\|=1$ は明らかですね。また，

\|Ta\| = \left(\sum_{n=2}^\infty |a_n|^2\right)^{1/2}\le \|a\|=1

なので， $\|T\|=\sup_{\|a\|=1} \|Ta\| \le 1$ です。一方で， $b=(0,1,0,0,\dots)$ とすると， $\|b\|=1$ であり，

Tb = (1,0,0,0,\dots)

なので， $\|Tb\|=1$ です。これより， $\|T\|=\sup_{\|a\|=1} \|Ta\| =1$ となることが分かりますね。

例2（関数空間）

$L^1 (\R)$ を， $\int_\R |f(x)|\, dx<\infty$ となる関数 $f\colon \R\to \mathbb{C}$ 全体(をa.e.で同じものを同一視したもの)のなすノルム空間(バナッハ空間)とする。ただし， $\|f\| = \int_\R |f(x)|\, dx$ である。 $S,T\colon L^1(\R)\to L^1(\R)$ を

\begin{aligned} S&\colon f(x)\mapsto f(2x), \\ T&\colon f(x)\mapsto e^{-x}f(x)1_{[0,\infty)}(x)\end{aligned}

と定める。このとき， $\|S\|=1/2,\, \|T\|=1$ である。

まず $S$ について考えましょう。 $Sf(x)=f(2x)$ なので， $\|f\|=1$ とすると，

\int_\R |f(2x)|\, dx = \frac{1}{2} \int_\R |f(y)|\, dy=\frac{1}{2}

ですから，常に $\|Sf\|=1/2$ ですから， $\|S\|=1/2$ ですね。

また $T$ について， $\|f\|=1$ とすると，

\int_0^\infty e^{-x}|f(x)|\,dx\le \int_{-\infty}^\infty|f(x)|\,dx=1

なので， $\|T\|\le 1$ となります。一方で $f_n = n1_{[0,1/n]}$ と定めると， $\|f_n\|=1$ であり，

\begin{aligned}\int_0^\infty e^{-x}|f_n(x)|\,dx&=n \int_0^{1/n} e^{-x}\, dx \\ &= n (1-e^{1/n}) \xrightarrow{n\to\infty} 1 \end{aligned}

ですから， $\lim_{n\to\infty} \|Tf_n\|=1$ となります。故に， $\|T\| = \sup_{\|f\|=1} \|Tf\|=1$ が分かりますね。

例3（行列）

$\mathbb{C}^n$ を $a=(a_1,\dots, a_n)\in \mathbb{C}^n$ に対し，

\|a\| = \sqrt{\sum_{k=1}^n |a_k|^2}

と定めたノルム空間(ヒルベルト空間)とする。

$A$ を $n\times n$ の複素行列とし， $\mathbb{C}^n$ 上の作用素 $T_A \colon \mathbb{C}^n\to \mathbb{C}^n$ を $x\mapsto Ax$ で定義する。このとき， $\|T_A\|$ は $AA^*$ の最大固有値の平方根に一致している。

解説については，ここでは省略します。

作用素ノルムその他の性質

作用素の合成とノルム
作用素の空間の完備性

の2つを紹介しましょう。

作用素の合成とノルム

定理2（作用素の合成とノルム）

$X,Y,Z$ をノルム空間とし， $S\in \mathcal{L}(X,Y),\, T\in\mathcal{L}(Y,Z)$ とする。このとき， $S$ と $T$ を合成して得られる作用素 $TS(=T\circ S)$ は $TS\in\mathcal{L}(X,Z)$ であり，

\color{red} \|TS\|_{\mathcal{L}(X,Z)}\le \|T\|_{\mathcal{L}(Y,Z)} \|S\|_{\mathcal{L}(X,Y)}

が成立する。

証明

作用素ノルムの定義の後に述べたように，一般に $\|Tx\|\le \|T\|\|x\|$ である。よって $x\in X$ に対し，

\|TSx\|\le \|T\| \|Sx\|\le \|T\| \|S\| \|x\|

であるから， $\|TS\|\le \|T\|\|S\|$ である。

証明終

作用素の空間の完備性

バナッハ空間とは，完備なノルム空間のことです。

定理3（作用素ノルムと完備性）

$X$ をノルム空間， $Y$ をバナッハ空間とする。このとき， $\mathcal{L}(X,Y)$ はバナッハ空間となる。

特に， $X$ の双対空間 $X^*=\mathcal{L}(X,\mathbb{C})$ はバナッハ空間になります。 $\mathbb{C}$ が完備だからですね。

示すべきことは， $\mathcal{L}(X,Y)$ が完備になることですね。証明しましょう。

証明

$\{T_n\}\subset \mathcal{L}(X,Y)$ をコーシー列とする。このとき， $x\in X$ に対し，

\begin{aligned}\|T_mx-T_nx\|_Y &= \|(T_m-T_n)x\|_Y \\&\le \|T_m-T_n\| \|x\|_X\\&\xrightarrow{m,n\to\infty} 0 \end{aligned}

であるから， $\{T_n x\}\subset Y$ はコーシー列である。 $Y$ はバナッハ空間なので， $\|T_n x-y\|\xrightarrow{n\to\infty}0$ となる $y\in Y$ が存在する。

そこで， $Tx=y$ となる作用素 $T\colon X\to Y$ を定めると，これが線形で， $D(T)=X$ となることは簡単にわかる。 $T$ が有界であることを示そう。 $\{ T_n\}$ はコーシー列より， $\|T_n\|\le L$ となる $L>0$ が存在する(証明は収束する数列は有界であることの証明とほぼ同じ)。