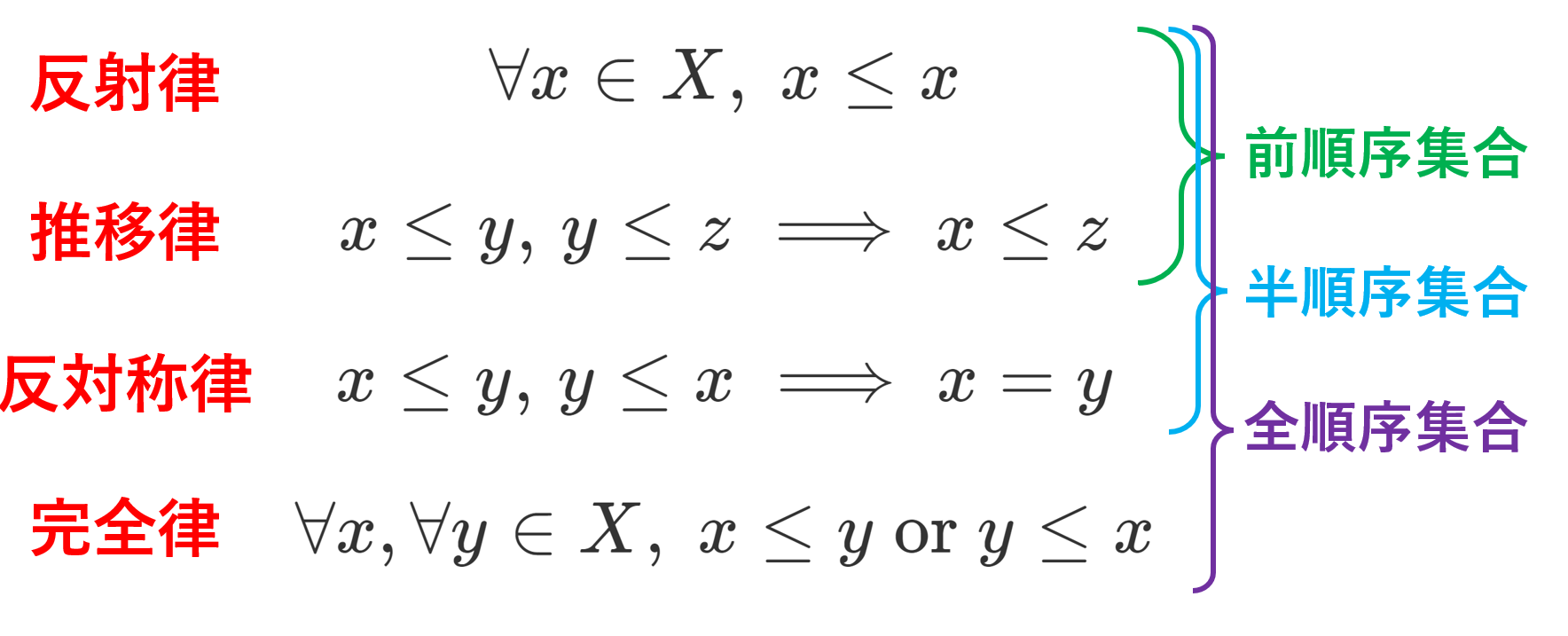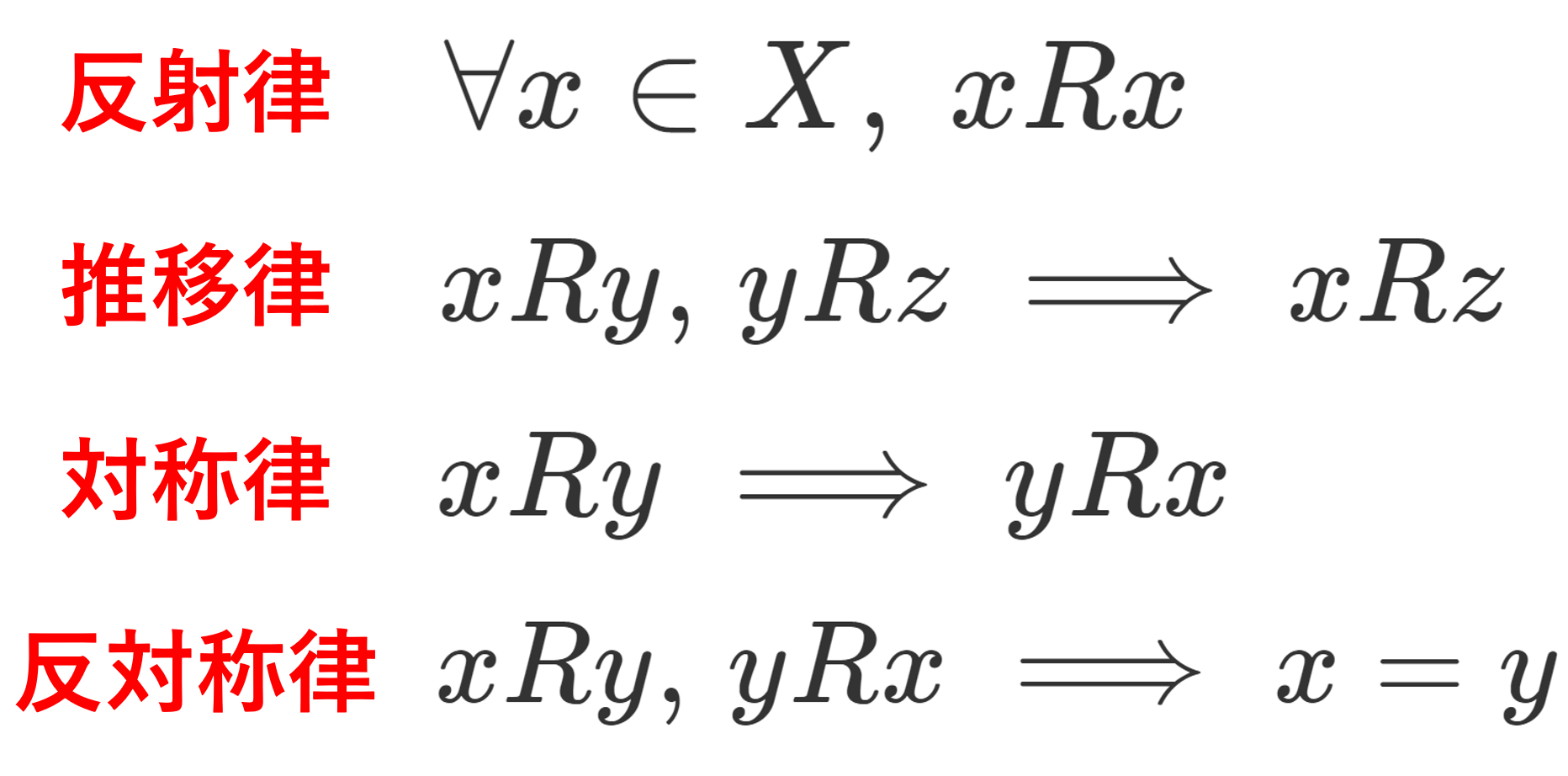半順序集合・全順序集合といった「順序集合」とは,集合内に順序(いわゆる大小関係)が定まった集合といえます。これらについて,その定義と具体例4つを紹介し,「順序を保つ写像」など,それに関連した知識も紹介します。
半順序集合・全順序集合
まずは,前順序集合・半順序集合・全順序集合を定義し,その具体例を考えましょう。
前順序集合・半順序集合・全順序集合の定義
定義(前順序集合・半順序集合・全順序集合)
空でない集合 X 上の4つの二項関係 \le について,
- 任意の x\in X に対して, x\le x (反射律)
- x,y,z\in X に対して, x\le y,\, y\le z ならば x\le z (推移律)
- x,y\in X に対して, x\le y ,\, y\le x ならば x=y (反対称律)
- 任意の x,y\in X に対して, x\le y または y\le x (完全律)
のうち,1,2 をみたすものを前順序集合 (preorderd set),1,2,3 をみたすものを半順序集合 (順序集合; partially ordered set; poset),1,2,3,4をみたすものを全順序集合 (totally ordered set)という。
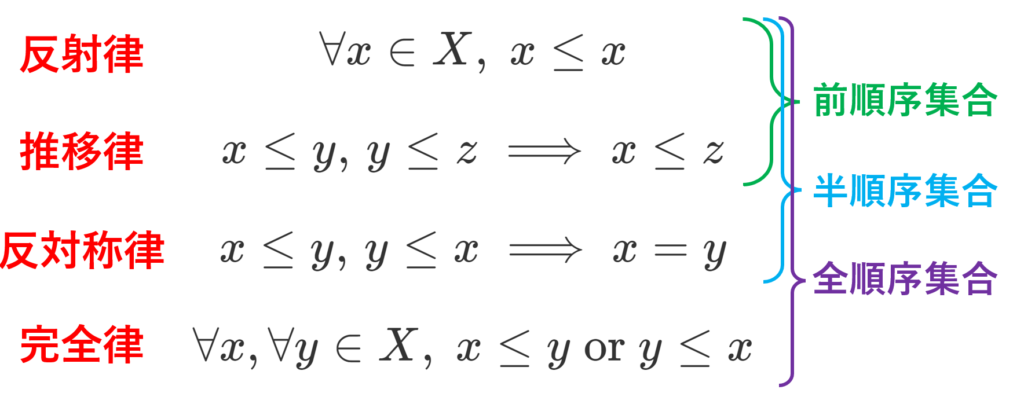
定義から明らかに,全順序集合なら半順序集合であり,半順序集合なら前順序集合です。
用語の使い方としては, X を半順序集合といったり,二項関係の記号を明示して, (X,\le ) を半順序集合と言ったりします。このとき,二項関係 \le を「半順序関係」ということもあります。
また,表記法について, x\le y と同じ意味で,\color{red} y\ge x と書いたり, x\le y かつ x\ne y ならば, \color{red}x<y や \color{red}x>y と書くこともあります。
数学では,一般の順序集合を扱うときは,特に半順序集合を扱うことが多いイメージがあります(偏見)。
前順序集合・半順序集合・全順序集合の具体例
定義だけ見てもさっぱりかもしれません。具体例を見るのが手っ取り早いでしょう。
例1.
実数の集合 \mathbb{R} は,通常の大小関係 \le によって,全順序集合である。
上で定義した4つの性質をすべて満たすので,全順序集合ですね。
例2.
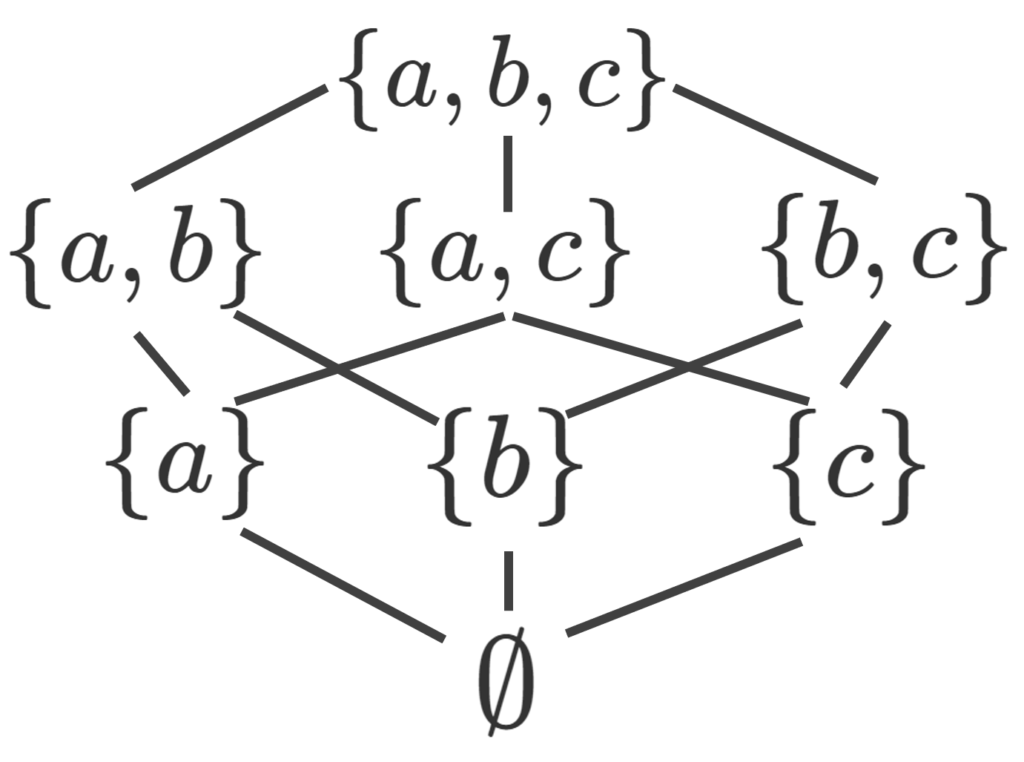
二元以上の集合 X に対して,そのべき集合 2^X は,包含関係 \subset により,半順序集合になるが,全順序集合ではない。
任意の A,B,C\in 2^X に対して, A\subset A であるし, A\subset B, \,B\subset C\implies A\subset C であるし, A\subset B,\, B\subset A\implies A=B ですから,半順序集合ですね。
一方で,例えば異なる一元集合 \{a\}, \{b\} の間には包含関係がありませんので,完全律は成り立ちません。よって,全順序集合ではないです。
たとえば, X=\{a,b,c\} のような3つの元からなる集合の場合,順序関係を図にすると以下のようになります。下から上の線が,包含関係による順序を意味します。半順序集合の代表的な例です。
例3.
f\colon \mathbb{R} \to \mathbb{R} のような関数の集合 F(\mathbb{R},\mathbb{R}) において, f\le g を,任意の x\in\mathbb{R} に対して f(x)\le g(x) であると定義すると,これは半順序集合になるが,全順序集合でない。
f\le f は明らかで, f\le g, \,g\le h であれば, f\le h も明らかでしょう。また, f\le g, \, g\le f が成り立てば,任意の x に対して f(x)=g(x) となりますから, f=g です。以上から,半順序集合になりますね。
一方で, f(x)=x と g(x)=1 は順序関係が定まりませんから,全順序集合ではないです。
例4.
例3.で定義した関数のうち,任意の点で f(x) \ne 0 となる集合 F(\mathbb{R},\mathbb{R}\setminus \{0\}) について, f\le g であることを
\limsup_{x\to\infty}\left| \frac{f(x)}{g(x)}\right|\le 1
と定義すると,これは前順序集合になるが,半順序集合や全順序集合ではない。
f\le f は明らかで, f\le g, \, g\le h とすると,
\begin{aligned} \limsup_{x\to\infty} \left| \frac{f(x)}{h(x)} \right|&= \limsup_{x\to\infty} \left| \frac{f(x)}{g(x)}\right| \left|\frac{g(x)}{h(x)} \right| \\ &\le \limsup_{x\to\infty} \left| \frac{f(x)}{g(x)}\right| \limsup_{x\to\infty} \left|\frac{g(x)}{h(x)} \right| \\ &\le 1 \end{aligned}
ですから, f\le h が成り立ちます。よって前順序集合です。
一方で, f(x)=x, \; g(x)=|x| とすると, f\le g,\, g\le f は成り立ちますが, f\ne g ですから,反対称律は成立しません。よって,半順序集合や全順序集合ではありません。
順序集合の関連する知識
順序集合を扱うにあたって,よく出てくる概念を紹介しましょう。
順序を保つ写像と順序同型
定義(順序を保つ写像・順序同型)
X,Y を半順序集合とする。 f\colon X\to Y に対して,
\color{red} x\le y \implies f(x)\le f(y)
であるとき, f を順序を保つ写像 (order-preserving) という。
f\colon X\to Y が全単射であり, f, f^{-1} がともに順序を保つ写像であるとき, X と Y は順序同型 (order isomorphic) であるといい, f を順序同型写像 (order isomorphism) という。
例を見てみましょう。
例5.
整数全体の集合 \mathbb{Z} と2の倍数全体の集合 2\mathbb{Z} は,通常の大小関係により順序同型である。
f(n)=2n とすると, f\colon \mathbb{Z}\to 2\mathbb{Z} は順序同型ですね。
例6.
正の整数全体の集合 \mathbb{N} と整数全体の集合 \mathbb{Z} と有理数全体の集合 \mathbb{Q} と実数全体の集合 \mathbb{R} は通常の大小関係により,どの2つも順序同型ではない。
\mathbb{R} はその他3つと濃度が違うので,全単射が構成できず,順序同型になり得ません(→可算集合と非可算集合(可算無限・非可算無限))。
また, \mathbb{N} は最小元 1 があるため,順序同型写像 f があれば f(1) は最小元でなければなりません。一方で, \mathbb{Z},\mathbb{Q} は最小元がないため,順序同型にはなりませんね。
残りは \mathbb{Z} と \mathbb{Q} が順序同型でないことですが,もし順序同型写像 f\colon \mathbb{Z}\to \mathbb{Q} があれば, f(0), f(1)\in \mathbb{Q} の間に \mathbb{Q} の元はないですが,これは \mathbb{Q} の稠密性に矛盾します(→有理数・無理数の稠密性の定義とその証明)。よって,順序同型ではないですね。
最大元・最小元・極大元・極小元・上界・下界・上限・下限
順序が付けられるということは,最大や最小を考えることができるということです。これについて,定義していきましょう。
定義(最大元・最小元・極大元・極小元・上界・下界・上限・下限)
X を半順序集合とし, A\subset X とする。
- x が A の最大元 (maximum element) であるとは, x\in A かつ任意の a\in A に対して, a\le x となることを言う。
- x が A の最小元 (minimum element) であるとは, x\in A かつ任意の a\in A に対して, x\le a となることを言う。
- x が A の極大元 (maximal element) であるとは, x\in A かつ x<a となる a\in A が存在しないことを言う(すなわち任意の a\in A に対して, a\le x または比較不可能)。
- x が A の極小元 (minimal element) であるとは, x\in A かつ a<x となる a\in A が存在しないことを言う(すなわち任意の a\in A に対して, x\le a または比較不可能)。
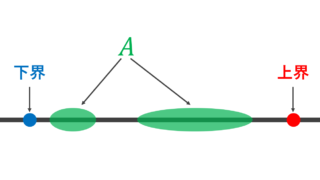
- x が A の上界 (upper bound) であるとは,任意の a\in A に対して, a\le x であることを言う。
- x が A の下界 (かかい; lower bound) であるとは,任意の a\in A に対して, x\le a であることを言う。
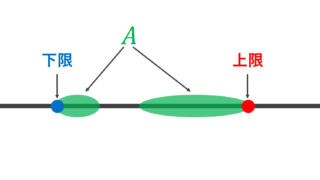
- x が A の上限 (supremum) であるとは, A の上界全体の集合の最小元であることを言い,存在すれば, \color{red}x=\sup A とかく。
- x が A の下限 (infimum) であるとは, A の下界全体の集合の最大元であることを言い,存在すれば, \color{red}x=\inf A とかく。
上の定義から,最大元はつねに極大元であることが分かります。また,上限が A に含まれていれば,それは最大元になります。
ある集合に対して,最大元・最小元・極大元・極小元・上界・下界・上限・下限が存在するか否かは分かりません。存在する場合もあるし,存在しないかもしれません。
簡単な例を考えましょう。
例7.
X=\mathbb{Q} を通常の大小関係による全順序集合とし, A = \mathbb{Q} \cap (0, \sqrt{2}) とする。
- A に最大元・最小元は存在しない。
- \sup A は存在せず, \inf A=0 である。
\sup A\ne \sqrt{2} なので注意してください。 \sqrt{2}\notin \mathbb{Q} です。
特別な順序集合
最後に,特別な順序集合をいくつか挙げておきましょう。
- 整列集合 …… 全順序集合のうち,任意の空でない部分集合が最小元をもつもの
- 帰納的半順序集合 …… 半順序集合のうち,任意の全順序部分集合が上界を持つもの
- 有向集合 …… 前順序集合(or 半順序集合)のうち,任意の二元部分集合に上界があるもの
- 束 …… 半順序集合のうち,任意の二元部分集合に上限と下限が存在するもの
- 完備束 …… 半順序集合のうち,任意の空でない部分集合に上限と下限が存在するもの
- 順序体 …… 全順序集合かつ体で, x\le y ならば x+z\le y+z であり,さらに 0\le z ならば xz\le yz が成り立つもの。