本記事では,名前の付いた,さまざまな確率分布についてまとめます。まだ数が少ないと思うかもしれませんが,随時追記します。
離散型確率分布
まずは,整数値をもつ離散型の確率分布を列挙しましょう。
ベルヌーイ分布
P(X=1) = p,\quad P(X=0) = 1-p.
離散一様分布
P(X=k) = \frac{1}{n}, \quad k=1,2,\ldots, n.
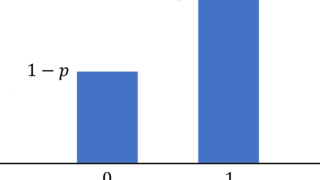
二項分布
\begin{aligned} &P(X=k) = {}_n\mathrm{C}_k\, p^k(1-p)^{n-k}, \\ &\hspace{90pt} k=0,1,2,\ldots,n.\end{aligned}
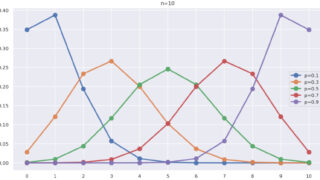
幾何分布
P(X=k) = (1-p)^{k-1} p ,\quad k\in\mathbb{Z}_{\ge 1}.
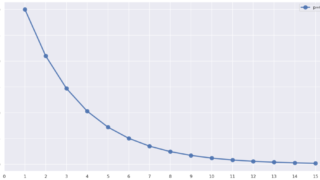
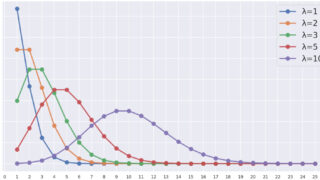
ポアソン分布
P(X=k) = \frac{\lambda^k}{k!}e^{-\lambda},\quad k\in\mathbb{Z}_{\ge 0}.
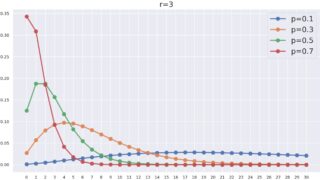
負の二項分布
P(X=k) = {}_{k+r-1}\mathrm{C}_k\, p^r(1-p)^k,\quad k\in \mathbb{Z}_{\ge 0}.
連続型確率分布
続いて,連続型の確率分布を列挙します。連続型の確率分布は,
P(X\in A) = \int_A p(x)\, dx
となる確率密度関数 p(x) が存在しているため,この確率分布を明記することにしましょう。
連続一様分布
p(x) = \frac{1}{b-a}, \quad a\le x\le b.
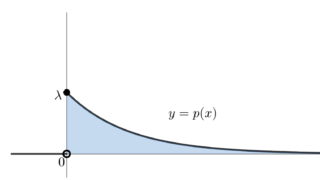
指数分布
p(x)=\lambda e^{-\lambda x},\quad x\ge 0.
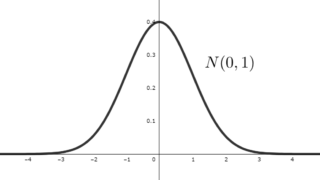
正規分布
p(x) = \frac{1}{\sqrt{2\pi \sigma^2}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}.
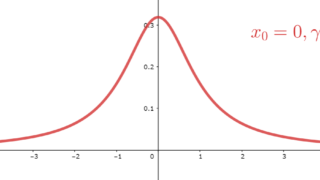
コーシー分布
p(x) = \frac{\gamma}{\pi\{(x-x_0)^2+\gamma^2\}}.
確率分布には,離散型・連続型の他に,特異型のものもあります。その他の分布についても,随時追加していきます。