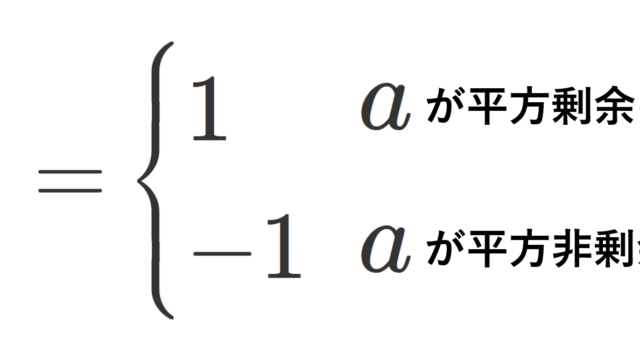 数論
数論 平方剰余・平方非剰余とルジャンドル記号
合同式における平方剰余(quadratic residue)・平方非剰余(quadratic nonresidue)の概念と,それを扱うのに便利なルジャンドル記号(Legendre symbol)の定義・性質について,順を追って解説していきましょう。
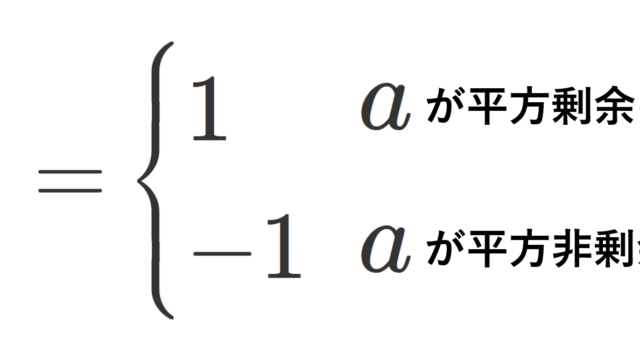 数論
数論  線形代数学
線形代数学  線形代数学
線形代数学  線形代数学
線形代数学 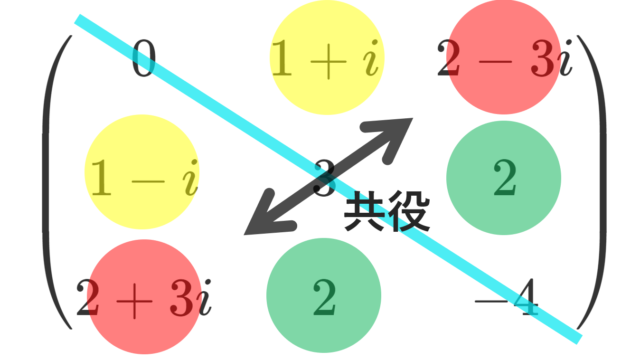 線形代数学
線形代数学 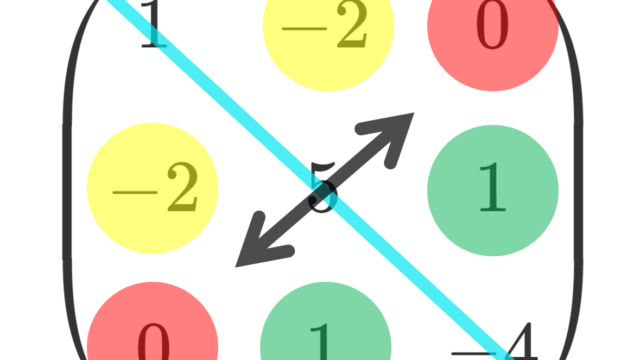 線形代数学
線形代数学 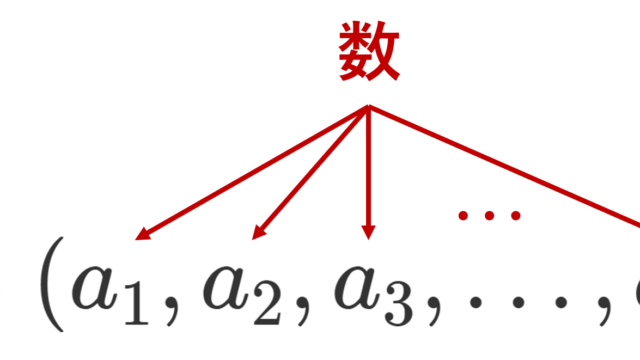 線形代数学
線形代数学 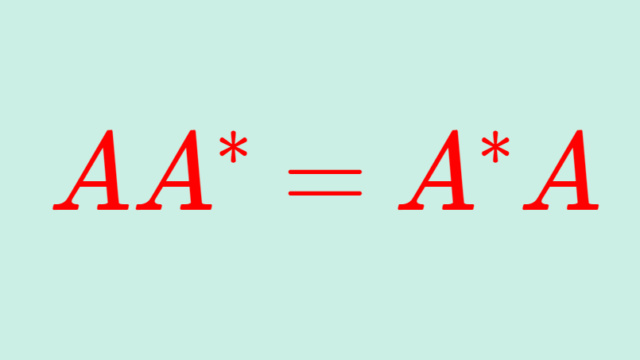 線形代数学
線形代数学 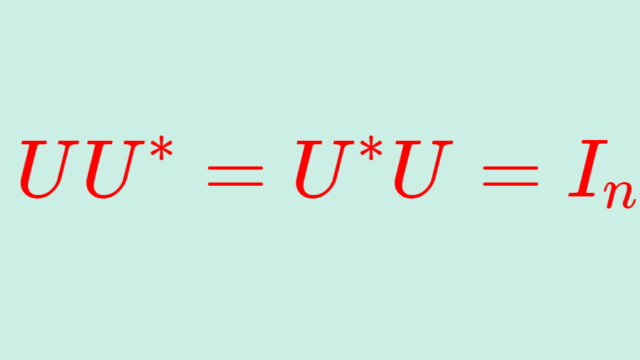 線形代数学
線形代数学 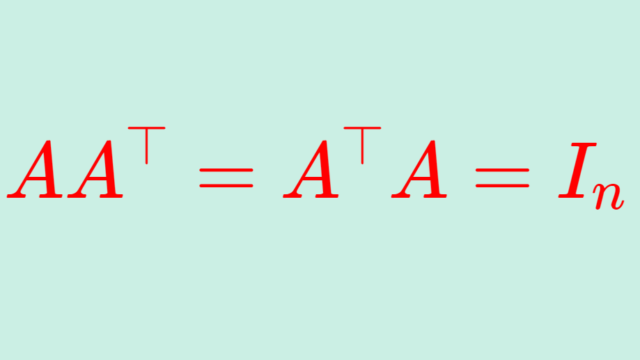 線形代数学
線形代数学