 確率論
確率論 コーシー分布の定義と性質とその証明
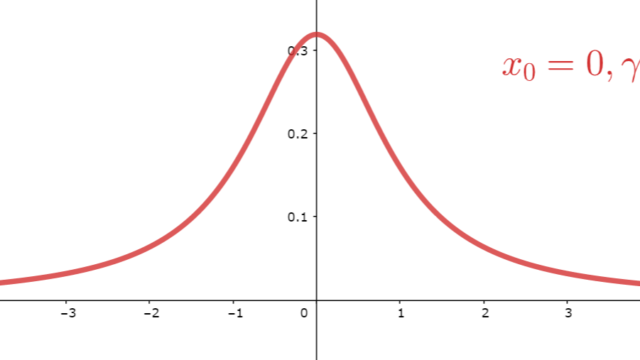
コーシー分布 (Cauchy distribution) は,期待値が定義できず,正規分布より減衰が遅い,裾の厚い分布(裾の重い分布)として有名です。確率密度関数はp(x) = 1/π(x^2+1)となります。これについて,その定義と性質の証明を詳しく述べましょう。
 確率論
確率論  集合と位相
集合と位相  集合と位相
集合と位相  記号・記法
記号・記法 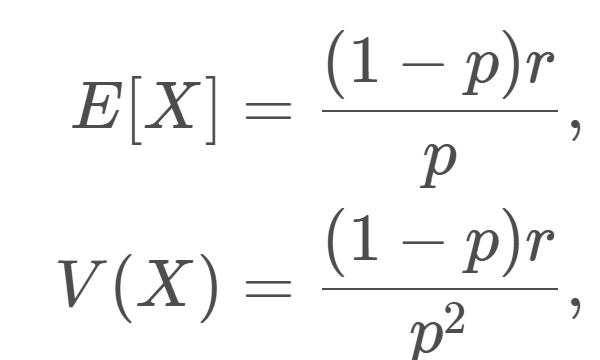 確率論
確率論 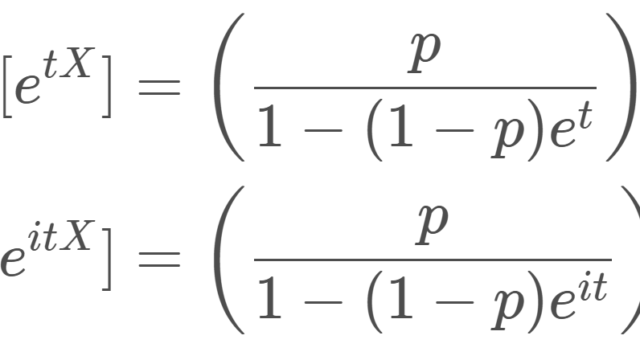 確率論
確率論 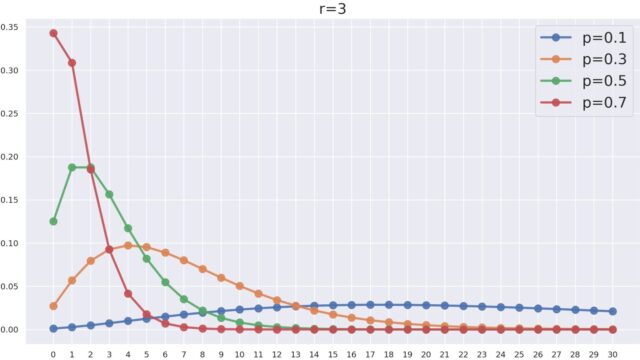 確率論
確率論 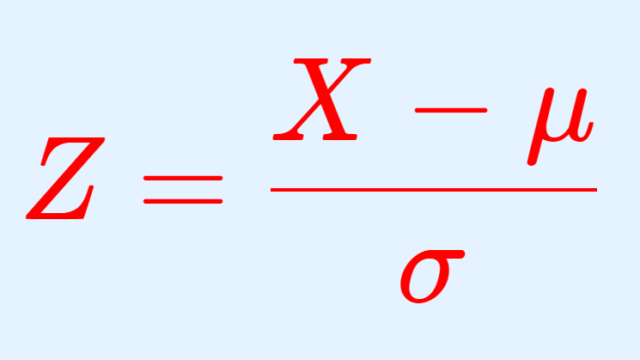 確率論
確率論  確率論
確率論  確率論
確率論