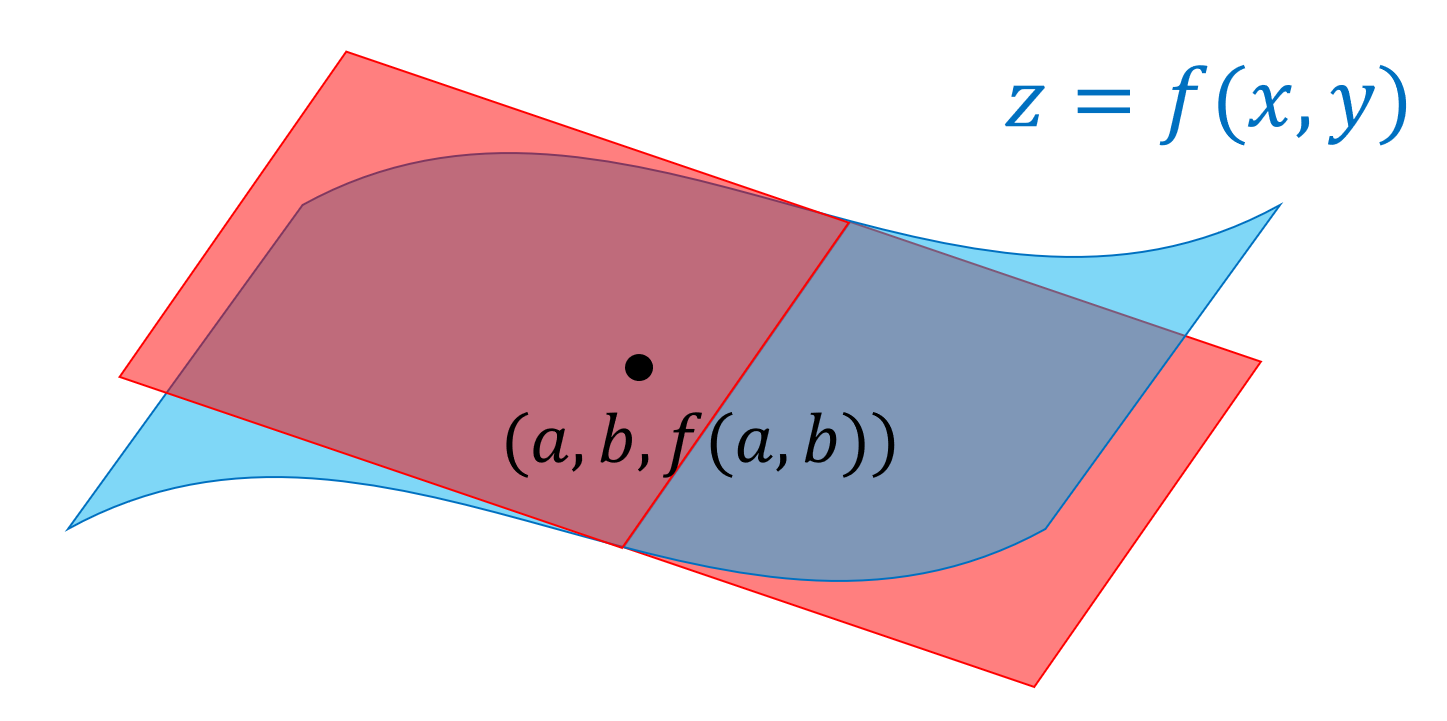
曲面 z=f(x,y) の (a,b,f(a,b)) における接平面の方程式は
z\!= \!f_x(a,b)(x-a)\!+\!f_y(a,b)(y-b)\!+\!f(a,b)
であり,曲面 f(x,y,z)=0 の点 (a,b,c) における接平面の方程式は
となります。これについて,その導出の解説を行いましょう。
接平面の方程式
そもそも点 \boldsymbol{x} における「接平面」とは,点 \boldsymbol{x} における接線たちが作る平面を指します。
接平面の方程式を2つ述べましょう。以下で, f_x,f_y, f_z は偏微分を指します(→偏微分とは~定義と例題と図形的意味~)。
定理1(接平面の方程式1)
f(x,y) を C^1 級とする。平面 z=f(x,y) の点 (a,b,f(a,b)) における接平面の方程式は
\color{red} z\!= \!f_x(a,b)(x-a)\!+\!f_y(a,b)(y-b)\!+\!f(a,b).定理2(接平面の方程式2)
f(x,y,z) を C^1 級とし, (a,b,c) のまわりで \operatorname{grad} f(= (\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} , \frac{\partial f}{\partial z} ) )\ne \boldsymbol{0} とする。このとき,点 (a,b,c) における接平面の方程式は
\small \color{red}f_x(a,\!b,\!c)\!(x\!\!-\!\!a)\!\!+\!\!f_y( a,\!b,\!c )\!(y\!\!-\!\!b)\!\!+\!\!f_z( a,\!b,\!c )\!(z\!\!-\!\!c)\!=\!0 .
また, \boldsymbol{x}=(x,y,z),\; \boldsymbol{a}=(a,b,c) と書き直すと,ベクトルの内積を用いて
とも表せる。
C^1 級とは, f_x,f_y が存在して,ともに連続であることを意味します(→C1級,Cn級,C∞級関数の定義と具体例5つ)。また, \operatorname{grad} f は勾配 (gradient) といい,\operatorname{grad} f = \left(\dfrac{\partial f}{\partial x}, \dfrac{\partial f}{\partial y} , \dfrac{\partial f}{\partial z} \right) と定義されます(→勾配(grad)の定義と意味)。
接平面の方程式2について, \operatorname{grad} \ne \boldsymbol{0} より,陰関数定理から, f(x,y,z)=0 が滑らかな曲面になることが保証されます。
接平面の方程式2は,1の一般化になっています。実際, g(x,y,z)= f(x,y)-z とおくと, g(x,y,z)=0\iff z=f(x,y) であり,またこのとき, \operatorname{grad} g= (*, *, -1)\ne \boldsymbol{0} ですから,定理2の仮定も満たしているため,ちゃんと2は1の一般化になっていますね。
接平面の方程式の導出証明
さて,各方程式の導出証明をしていきましょう。接平面の方程式2は1の一般化ですから2のみ証明すればよいのですが,あえて両方証明してみましょう。
接平面の方程式1(z=型)の導出証明
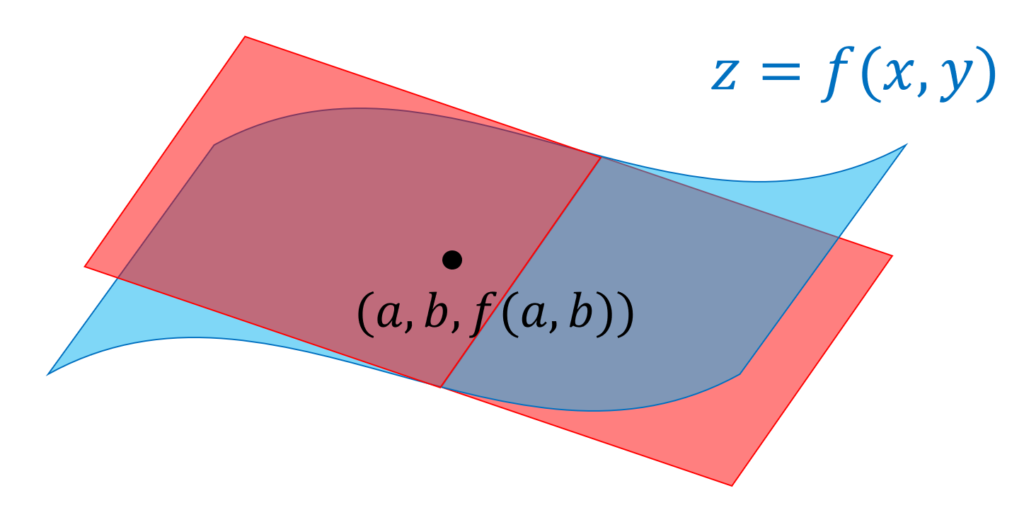
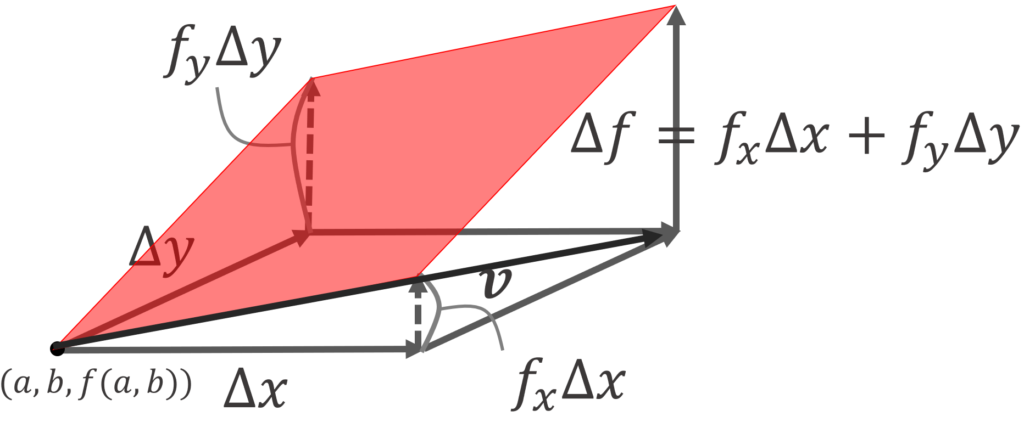
証明
f(x,y) は C^1 級であるから,特に全微分可能であり,点 (a,b) における \boldsymbol{v}= (\Delta x, \Delta y) 方向の方向微分 \nabla_{\boldsymbol{v}} f は,ベクトルの内積を用いて
\langle \operatorname{grad} f(a,b),\boldsymbol{v} \rangle = f_x(a,b)\Delta x+f_y(a,b)\Delta y
とかける(→方向微分とは~定義・性質・求め方を詳しく~)。これは,接平面の方程式が
であることを意味する。
証明終
接平面の方程式2(一般型)の導出証明
つづいて,一般系の証明も考えます。こちらは,接平面の法線ベクトルを考えます。
証明
曲面 f(x,y,z)=0 を M\subset \mathbb{R}^3 とする。このとき, (a,b,c) における曲面の法線ベクトルは \operatorname{grad} f(a,b,c) であることを示そう。
I\subset \mathbb{R} とし, \boldsymbol{r}\colon I\ni t \mapsto (x(t),y(t),z(t))\in M を, (a,b,c) を通る,曲面 M 上の滑らかな曲線とする。 \boldsymbol{r}(t) は曲面 M 上にあるから,f(x(t),y(t), z(t))=0 であり,この両辺を t で微分すると,
f_xx'(t)+f_yy'(t)+f_z z'(t)=0.
すなわち,ベクトルの内積を用いて \langle \operatorname{grad} f, \boldsymbol{r'}(t)\rangle=0 とかける。これは, \operatorname{grad} f は,接線方向 \boldsymbol{r'}(t) と垂直であることを意味する。よって, \operatorname{grad}f は曲面 M の法線ベクトルである。
ゆえに,接平面の方程式は, (a,b,c) を通り, \operatorname{grad}f(a,b,c) = (f_x(a,b,c), f_y(a,b,c), f_z(a,b,c)) を法線ベクトルとする平面の方程式であるから,
\small f_x(a,\!b,\!c)\!(x\!\!-\!\!a)\!\!+\!\!f_y( a,\!b,\!c )\!(y\!\!-\!\!b)\!\!+\!\!f_z( a,\!b,\!c )\!(z\!\!-\!\!c)\!=\!0
となる。
証明終
f(x,y,z)=0 の法線方向が \operatorname{grad} f であることについては,2次元のときに考えてみましょう。
2次元 f(x,y)=0 のときは,等高線をイメージして, \operatorname{grad} f は最大傾斜方向なので,等高線と垂直になりますね(→勾配(grad)の定義と意味)。今は,これの3次元版といえます。