正方行列における,上三角行列・下三角行列の定義とその性質6つを紹介します。
上三角行列・下三角行列(三角行列)の定義
定義(上三角行列・下三角行列)
A = (a_{ij}) を正方行列とする。
\color{red} i > j \implies a_{ij} = 0 が成立するとき,すなわち
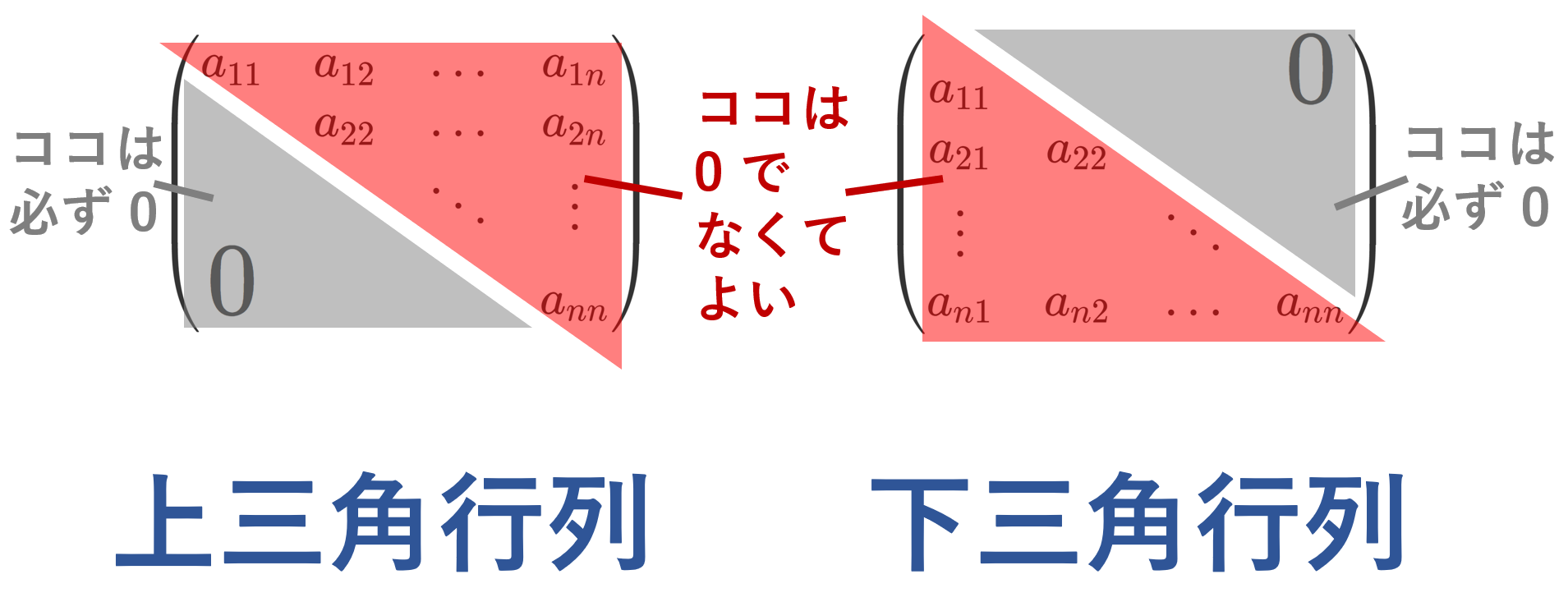
\color{red} A = \begin{pmatrix} a_{11} & a_{12} & \dots & a_{1n} \\ & a_{22} &\dots & a_{2n} \\ &&\ddots & \vdots \\ \huge{0}&&&a_{nn} \end{pmatrix}
のとき,これを上三角行列 (upper triangular matrix) あるいは右三角行列 (right triangular matrix) という。
逆に, \color{red} i < j \implies a_{ij} = 0 が成立するとき,すなわち
\color{red} A = \begin{pmatrix} a_{11} &&& \huge{0}\\ a_{21} & a_{22} \\ \vdots& & \ddots \\ a_{n1} & a_{n2} & \dots & a_{nn} \end{pmatrix}
のとき,これを下三角行列 (lower triangular matrix) あるいは左三角行列 (left triangular matrix) という。
上三角行列・下三角行列を合わせて三角行列 (triangular matrix) という。
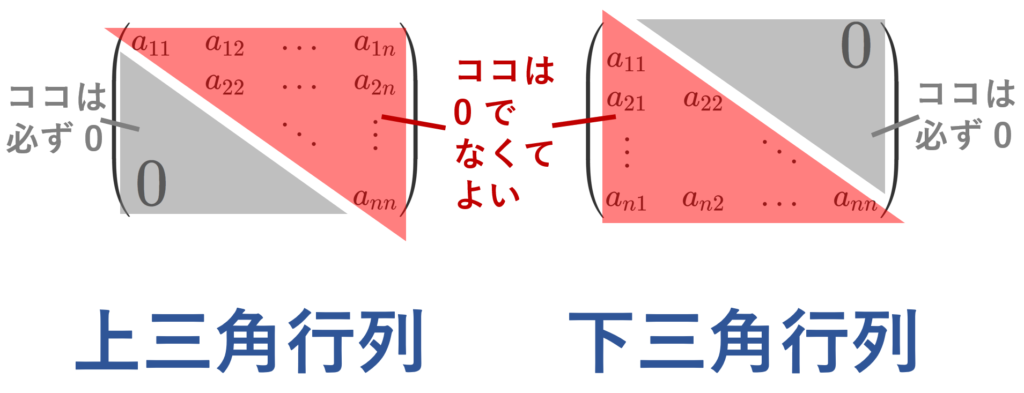
対角成分より下が 0 となる行列を上三角行列,対角成分より上が 0 となる行列を下三角行列というんですね。
上三角行列・下三角行列(三角行列)の具体例
簡単な具体例を挙げておきましょう。
三角行列の具体例
三角行列の性質
性質を挙げましょう。
定理(三角行列の性質)
A = (a_{ij}),\, B=(b_{ij}) を n 次の上三角行列とする。このとき,
- 上三角行列の和・定数倍もまた上三角行列である。
- AB = \begin{pmatrix} a_{11}b_{11} & * & \dots & * \\
& a_{22}b_{22} &\dots & * \\
&&\ddots & \vdots \\
\huge{0}&&&a_{nn}b_{nn}
\end{pmatrix}.
特に,上三角行列の積もまた上三角行列である。 - A^\top は下三角行列である(転置行列)。
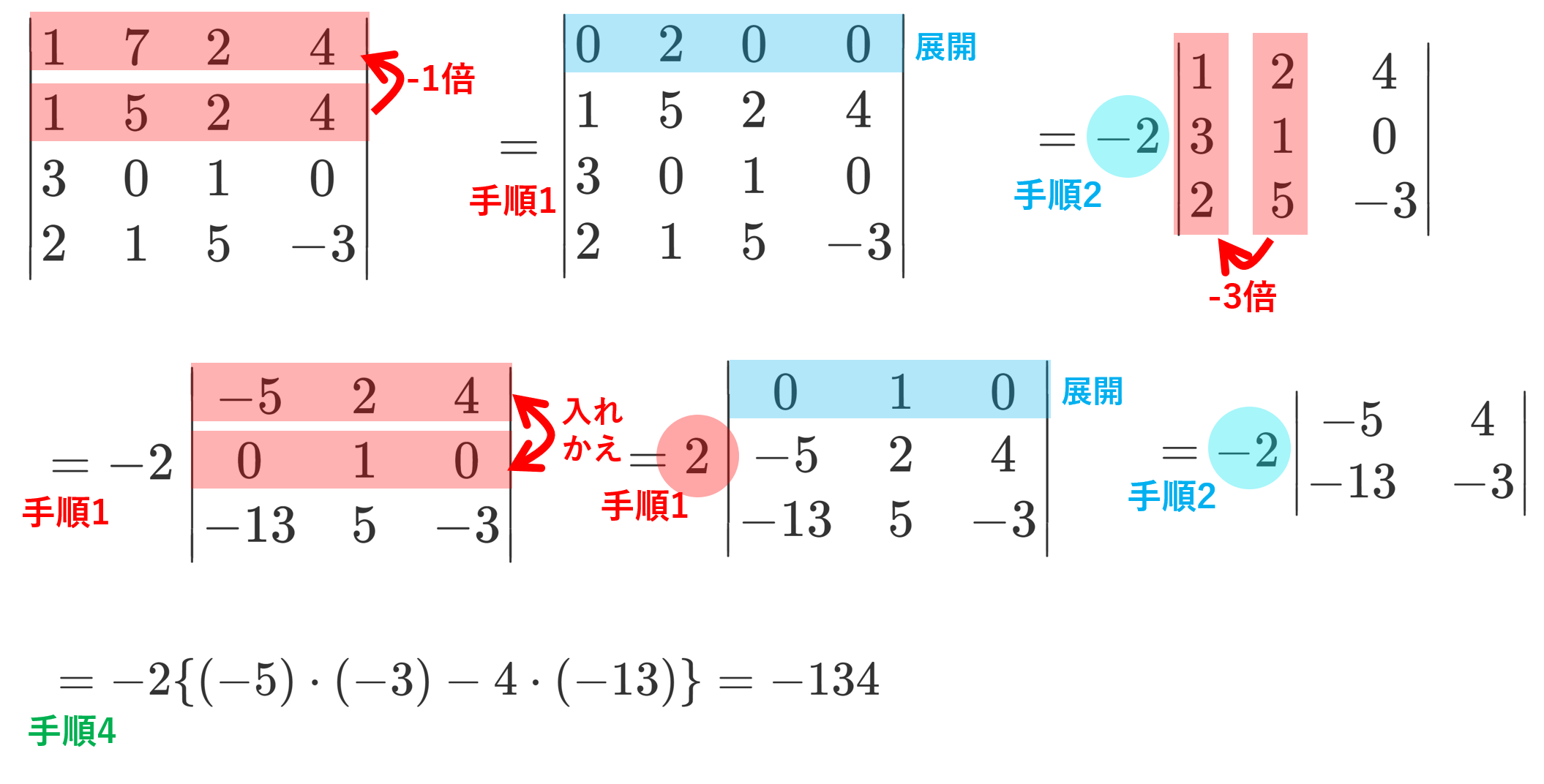
- \det A = a_{11} a_{22} \dots a_{nn}. (行列式)
- a_{ii} \ne 0 \,\, (1 \le i \le n) のとき, A^{-1} は
A^{-1} = \begin{pmatrix} a_{11}^{-1} & * & \dots & * \\ & a_{22}^{-1} &\dots & * \\ &&\ddots & \vdots \\ \huge{0}&&&a_{nn}^{-1} \end{pmatrix}
の形をしている。特に,上三角行列の逆行列は上三角行列である。 - A の固有値は a_{11}, a_{22}, \dots , a_{nn} である。
なお,すべての主張は「上三角行列」と「下三角行列」の言葉を入れ替えても全く同様に成立します。
証明は簡単なので省略します。
正方行列は三角化可能
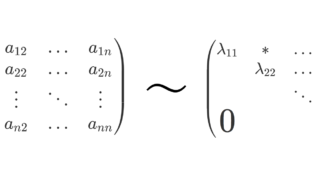
任意の正方行列は三角行列と相似であることが知られています。すなわち,任意の正方行列 A に対し,ある正則行列(可逆行列) P が存在して,P^{-1}AP は上三角行列にすることが可能です。
これについては,以下で解説しています。