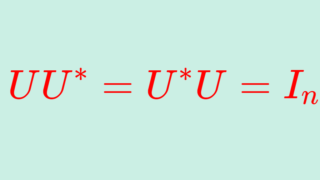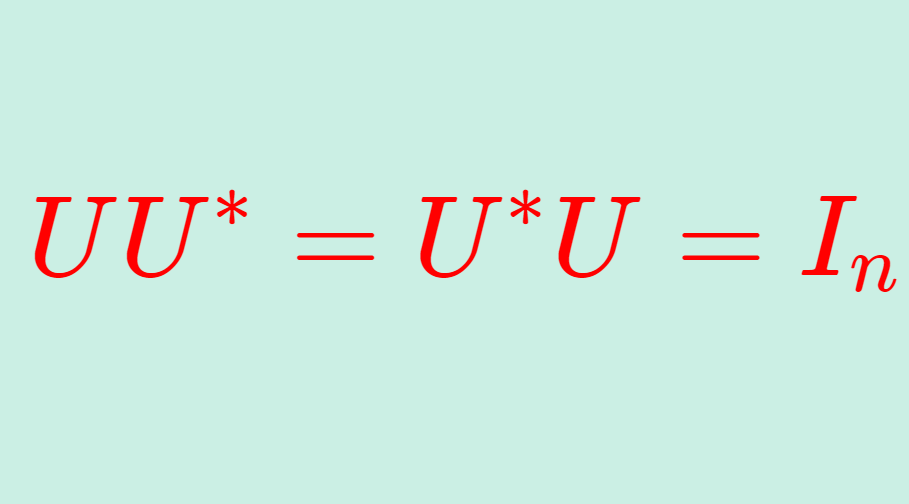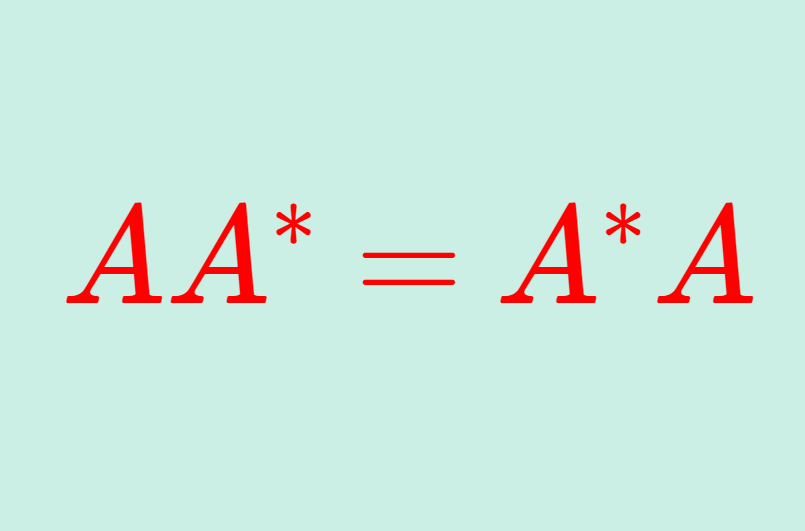任意の正方行列は,上三角行列と相似であることが知られています。これの証明を詳しく解説しましょう。
【行列の三角化】正方行列は三角行列と相似である
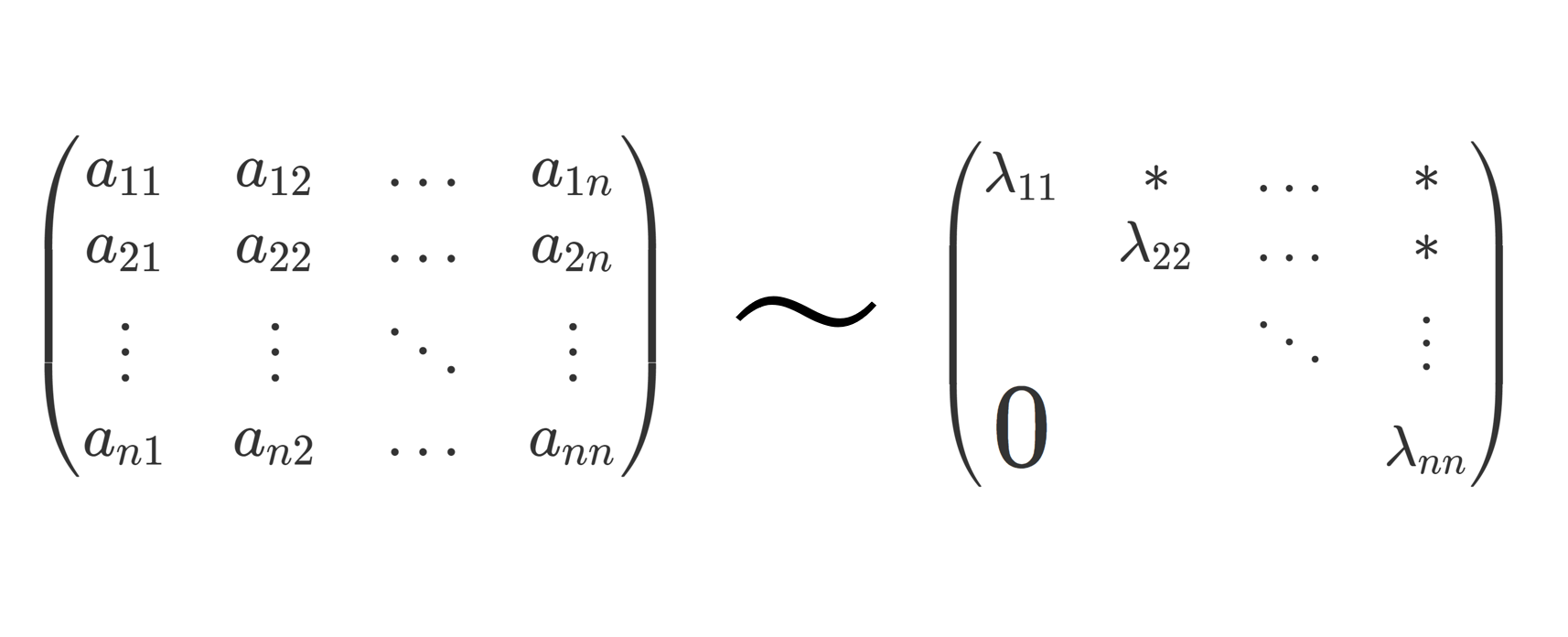
定理(正方行列は三角行列と相似)
\large\color{red} T= U^{-1} AUユニタリ行列とは, UU^*=U^*U=I となる行列,言い換えると U^{-1}=U^* ( U^* は随伴行列(共役転置))が成り立つ正方行列を指します。詳しくは,以下の記事で解説しています。
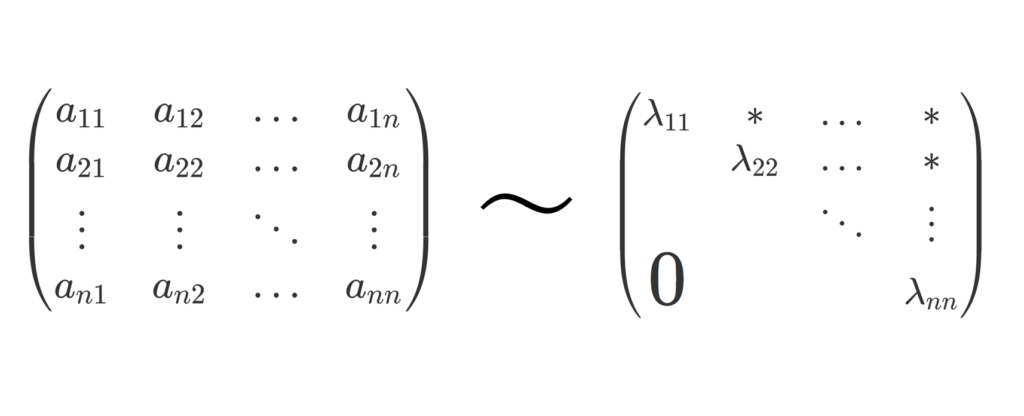
上三角行列とは,対角成分より上に成分が並ぶ行列
\begin{pmatrix} \lambda_{11}& * & \dots & * \\ & \lambda_{22} &\dots & * \\ &&\ddots & \vdots \\ \huge{0}&&&\lambda_{nn} \end{pmatrix}
のことをいいます。詳しくは,以下で解説しています。
注意ですが,「上三角行列と相似」というのは,「行基本変形によって上三角行列にできる」とは意味が違います。相似というのは, P^{-1}AP の形を考えますが,行基本変形というのは,基本行列を左からかけることに相当します。
【行列の三角化】正方行列は三角行列と相似であることの証明
証明
数学的帰納法により示す。n=1 次正方行列のときに成り立つのは明らか。
n-1 次正方行列のとき,証明できたとする。この下で n 次正方行列のときを考える。
A の固有値の1つを \lambda_1 とし,その固有ベクトルを \boldsymbol{x_1} \in\mathbb{C}^n とする。次に, \boldsymbol{x_1},\boldsymbol{x_2},\dots, \boldsymbol{x_n} が正規直交基底になるように \boldsymbol{x_2},\dots,\boldsymbol{x_n} を付加する。このとき,これらを列ベクトルとする正方行列
S = (\boldsymbol{x_1},\boldsymbol{x_2},\dots, \boldsymbol{x_n})
はユニタリ行列である(→ユニタリ行列の定義と性質10個とその証明)。すると, A\boldsymbol{x_1} = \lambda_1\boldsymbol{x_1} より, AS = S\begin{pmatrix} \lambda_1 & \ast \\ 0& A_1 \end{pmatrix},すなわち
とかける。ただし, A_1 は n-1 次正方行列である。帰納法の仮定により,あるユニタリ行列 T が存在して, T^{-1}A_1T は上三角行列になる。ここで,
とすると,列ベクトルは正規直交基底なので,これもユニタリ行列である。ここで,
は上三角行列である。したがって, U=ST_1 とおけば, U^{-1}AU は上三角行列になる。ユニタリ行列の積もユニタリ行列であるから, U はユニタリ行列であり,証明が終わる。
証明終
なお,相似変換をしても固有値は変わらないことと,三角行列は対角成分が固有値になることから,三角化後の対角成分に並ぶ数は元の正方行列の固有値になっているわけです。
また,元の行列が実行列であったとしても,三角化後の行列が実行列とは限りません。これは,実行列の固有値が実とは限らないことから分かりますね。
なお,実際に上三角行列を作るときも,この証明と同じ手順を辿ればよいです。要するに
- まず固有値と固有ベクトルを一つ求める。
- ベクトルを付加して,正規直交基底を作り,それにより, S^{-1}AS = \begin{pmatrix} \lambda_1 & 0 \\ 0& A_1\end{pmatrix} を作る。
- 正方行列 A_1 に対して,同じことを繰り返す。
とすればよいわけです。