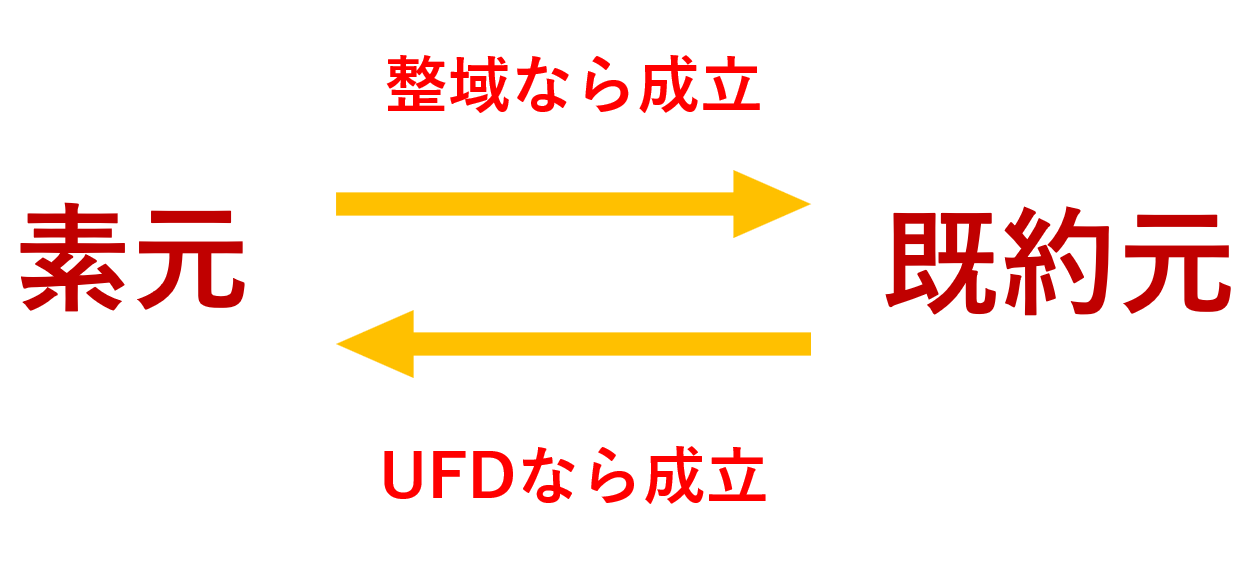
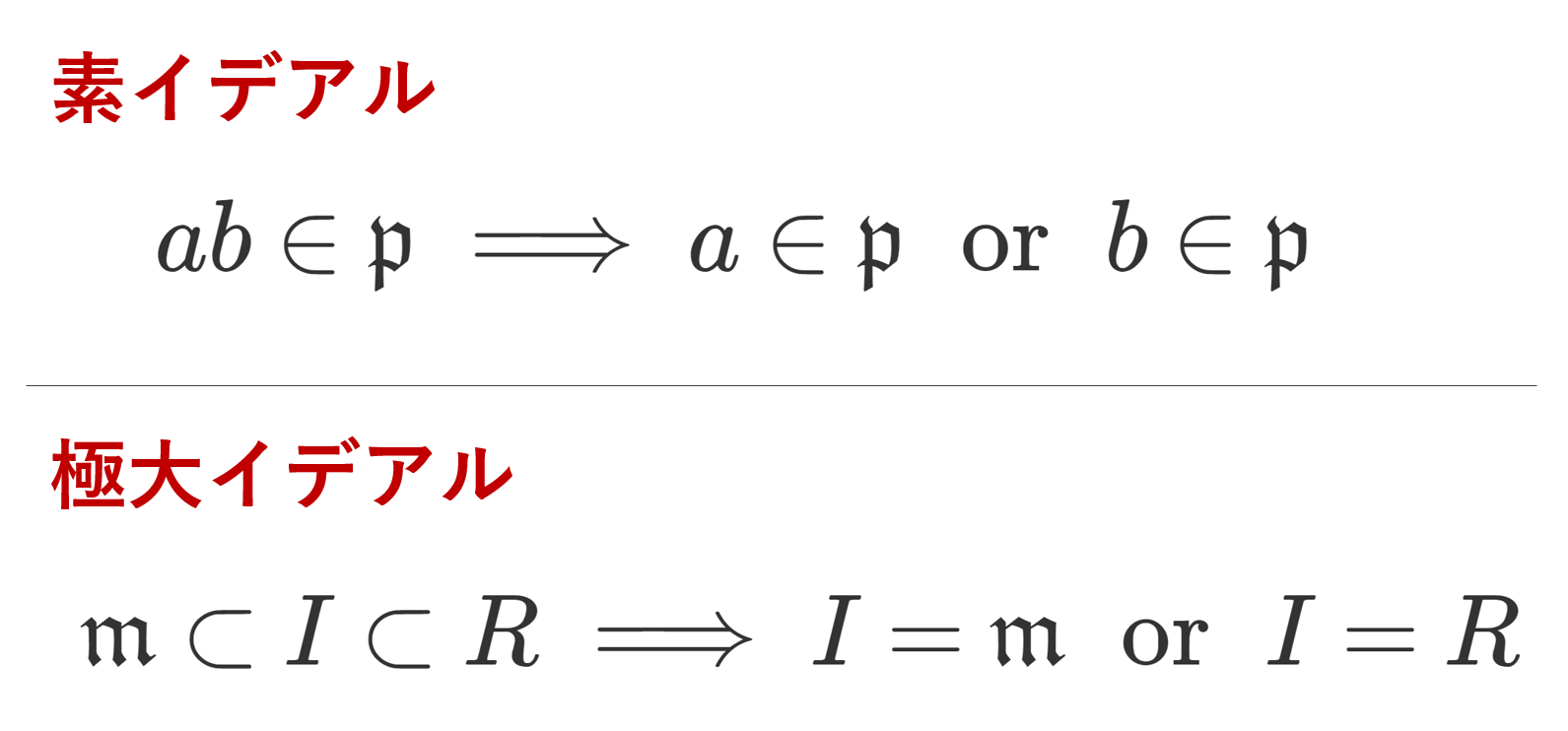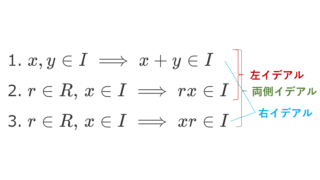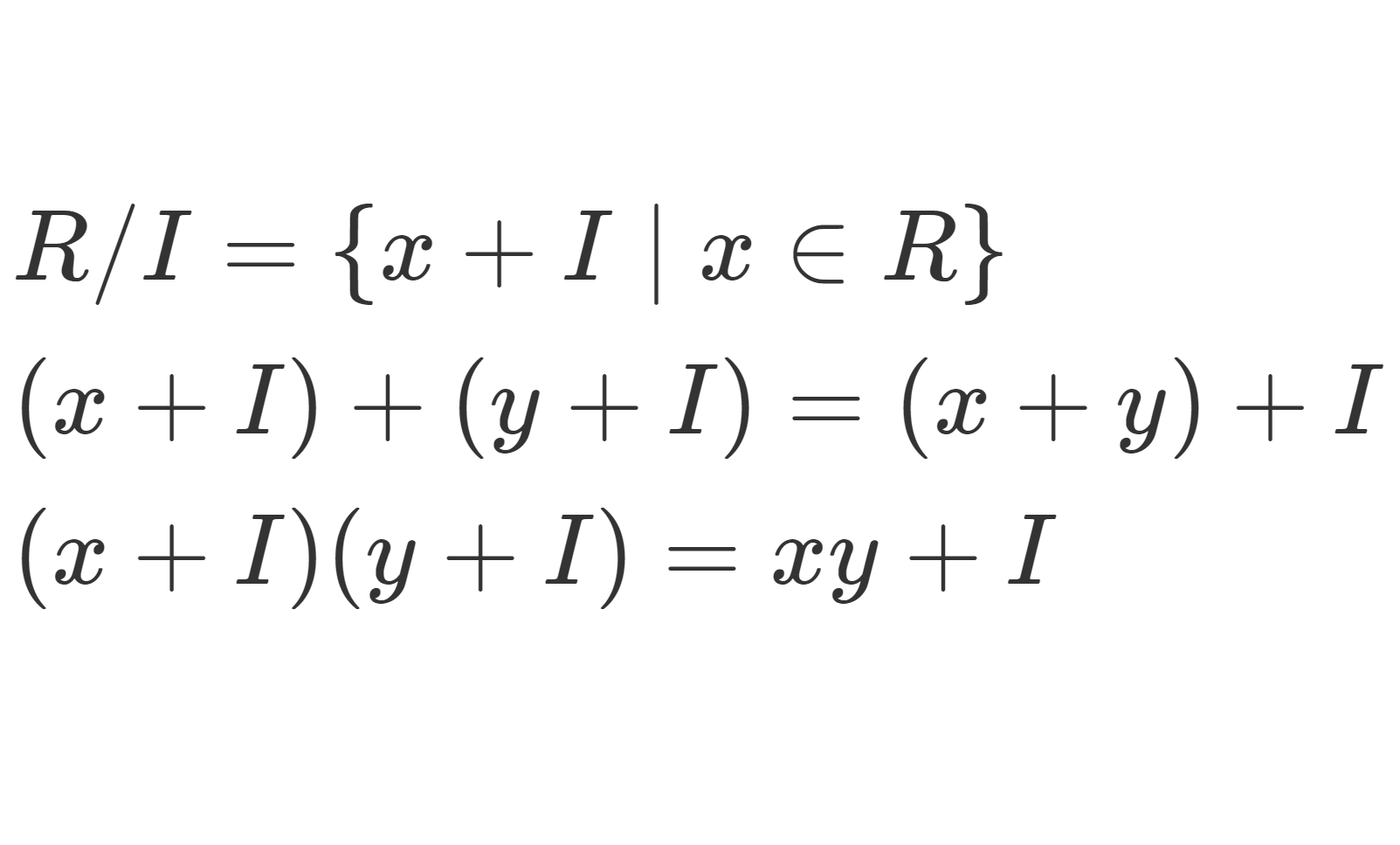可換環論における,素イデアルとは整数における素数の概念を拡張したものであり,極大イデアルとは,真のイデアルのうち,包含関係に関して極大なものを指します。
素イデアル・極大イデアルについて,その定義・具体例・性質を解説しましょう。
素イデアルと極大イデアルの定義
定義(素イデアル・極大イデアル)
R を可換環とする。
イデアル \mathfrak{p}\subsetneq R が素イデアル (prime ideal) であるとは, a,b\in R に対し,
\color{red}\large ab\in\mathfrak{p}\implies a\in\mathfrak{p}\;\text{ or }\; b\in\mathfrak{p}
が成り立つことをいう。
イデアル \mathfrak{m}\subsetneq R が極大イデアル (maximal ideal) であるとは,イデアル I に対し,
\large\color{red} \mathfrak{m}\subset I\subset R \implies I= \mathfrak{m}\;\text{ or }\; I=R
となることをいう。
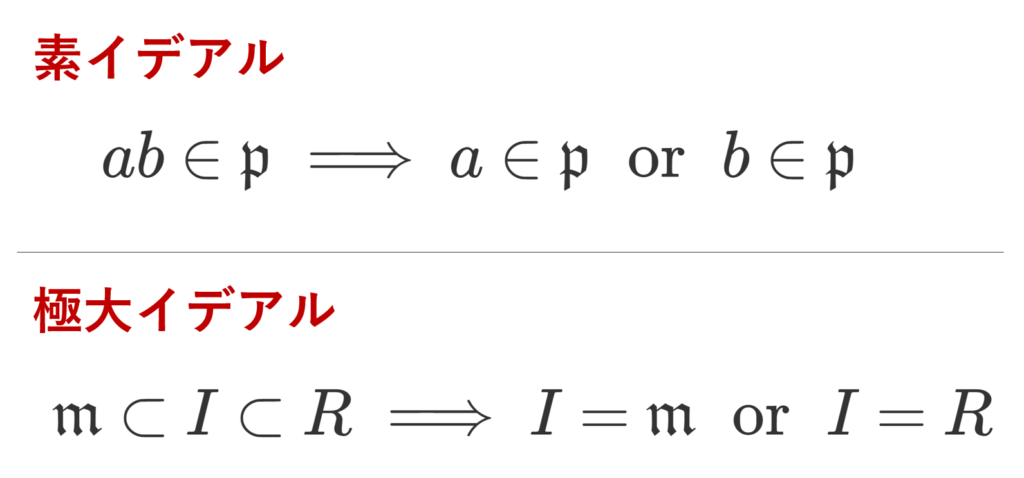
素イデアルの定義は,対偶を取って a,b\notin \mathfrak{p} \implies ab \notin \mathfrak{p} としても構いません。後の具体例で挙げますが,素イデアルは整数 \mathbb{Z} における素数の概念を一般化したものです。
極大イデアルの定義は, \mathfrak{m}\subsetneq I \subsetneq R となるイデアル I が存在しない,としても構いません。包含関係に関して極大ということですね。
素イデアル・極大イデアルに関する性質
いきなりですが,先に素イデアル・極大イデアルの性質を確認しましょう。
定理1(素イデアル・極大イデアルの性質)
R,S を可換環とする。
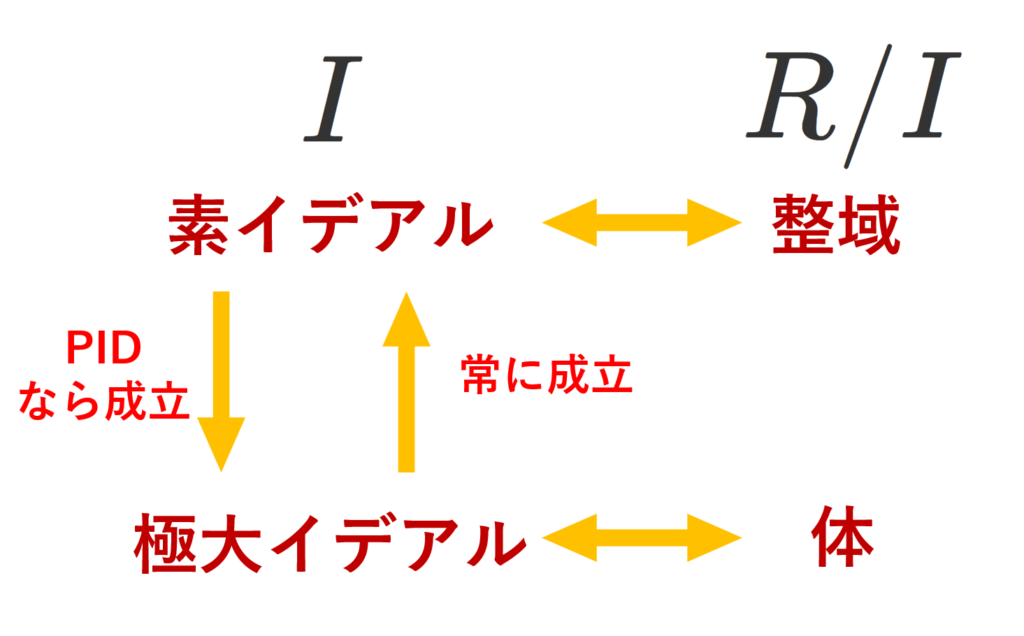
- \mathfrak{p}\subsetneq R が素イデアル \iff R/\mathfrak{p} が整域
- \mathfrak{m}\subsetneq R が極大イデアル \iff R/\mathfrak{m} が体
- I\subsetneq R が極大イデアルならば素イデアルである。
- 単項イデアル整域(PID)において,(0) \subsetneq \mathfrak{p}\subsetneq R が素イデアルならば,極大イデアルである。
- f\colon R\to S を準同型, \mathfrak{p}\subsetneq S を素イデアルとするとき, f^{-1}(\mathfrak{p})\subsetneq R も素イデアルである。
R/\mathfrak{p}, R/\mathfrak{m} などは剰余環(商環)の話です。
順番に証明してきましょう。
以下で, a\in R について, R/I の元 a+I を \overline{a} と略記することにします。逆に, \overline{a}\in R/I に対し,対応する R の代表元を一つ取ってこれますから,そのうちの任意の1つを a\in R とかきます。
1. pが素イデアル ⇔ R/pが整域
可換環 A が整域とは, a,b\in A に対し, ab=0\implies a=0\text{ or } b=0 が成立することを言います(→整域とは~定義・具体例4つ・基本的性質4つ~)。
証明
\mathfrak{p}\subsetneq R が素イデアル \implies R/\mathfrak{p} が整域について
\overline{a},\overline{b} \in R/\mathfrak{p} が \overline{a}\overline{b}=0 をみたすとする。これは, ab\in \mathfrak{p} を意味し, \mathfrak{p} は素イデアルなので, a\in \mathfrak{p} または b\in \mathfrak{p} である。これより, \overline{a}=0 または \overline{b} =0 である。
\mathfrak{p}\subsetneq R について, R/\mathfrak{p} が整域 \implies \mathfrak{p} が素イデアルについて
ab\in \mathfrak{p} とする。このとき,\overline{a}\overline{b}=0 であり, R/\mathfrak{p} は整域なので,\overline{a}=0 または \overline{b}=0 である。これより, a\in\mathfrak{p} または b\in\mathfrak{p} である。
証明終
2. mが極大イデアル ⇔ R/mが体
証明
\begin{aligned}\mathscr{I}_\mathfrak{m}&=\{\mathfrak{m}\subset I\mid I \text{ is ideal}\},\\ \mathscr{J}_\mathfrak{m}&=\{ J \subset R/\mathfrak{m} \mid J \text{ is ideal}\} \end{aligned}
とする(idealは「イデアル」の意味)。
準同型定理より,自然な射影 \pi \colon R\to R/\mathfrak{m} の引き起こす写像
\pi \colon \mathscr{I}_\mathfrak{m}\ni I \mapsto \pi(I)\in \mathscr{J}_\mathfrak{m}
は全単射である。 \mathfrak{m} が極大イデアル \iff \mathscr{I}_\mathfrak{m}=\{ \mathfrak{m}, R\} であり,
R/\mathfrak{m} が体 \iff \mathscr{J}_\mathfrak{m}=\{(0), R/\mathfrak{m}\} である(→イデアル(環論)とは~定義・具体例・基本的性質の証明~)から,題意は示された。
証明終
3. 極大イデアルならば素イデアルである
証明
体は整域であるから,1,2.より,
\mathfrak{m} が極大イデアル \iff R/\mathfrak{m} が体 \implies R/\mathfrak{m} が整域 \iff \mathfrak{m} が素イデアル
である。
証明終
4. 単項イデアル整域では,真の素イデアルは極大イデアルである
証明
R を単項イデアル整域(PID) とする。(p)\subsetneq R を素イデアルとし, (p)\subset (a)\subset R とする。 p\in (a) より, p=ab となる b\in R が存在する。
ab\in (p) より, a\in (p) または b\in (p) である。 a\in (p) のときは, (a)\subset (p) から, (a)=(p) となる。
b\in (p) のときは, b=pc となる c\in R が存在する。よって, p=ab=apc=pac であり, ac=1 である。ゆえに, a\in R^{\times} ( a は単元(可逆元))であり, (a)=R である。
以上から, (a)=(p) または (a)=R となり, (p) は極大イデアルである。
証明終
5. 素イデアルの引き戻しが素イデアルであること
示すべきは, \mathfrak{p}\subsetneq S が素イデアル, f\colon R\to S が準同型であるとき,f^{-1}(\mathfrak{p})\subsetneq R が素イデアルであることです。
証明
f^{-1}(\mathfrak{p})\subsetneq R がイデアルであることはイデアル(環論)とは~定義・具体例・基本的性質の証明~中で示した。
ab\in f^{-1}(\mathfrak{p}) とする。このとき, f(a)f(b)=f(ab)\in\mathfrak{p} より, f(a)\in\mathfrak{p} または f(b)\in\mathfrak{p} である。
ゆえに, a\in f^{-1}(\mathfrak{p}) または b\in f^{-1}(\mathfrak{p}) が成り立つため, f^{-1}(\mathfrak{p}) は素イデアルである。
証明終
なお,極大イデアルの引き戻しは極大イデアルとは限りません。たとえば,包含写像 \iota \colon \mathbb{Z}\to \mathbb{R} は準同型あり,\mathbb{R} は体なので, \mathbb{R} の極大イデアルは (0) のみです。ただ, \iota^{-1}((0))=(0)\subset\mathbb{Z} は極大イデアルではありません。
素イデアル・極大イデアルの具体例
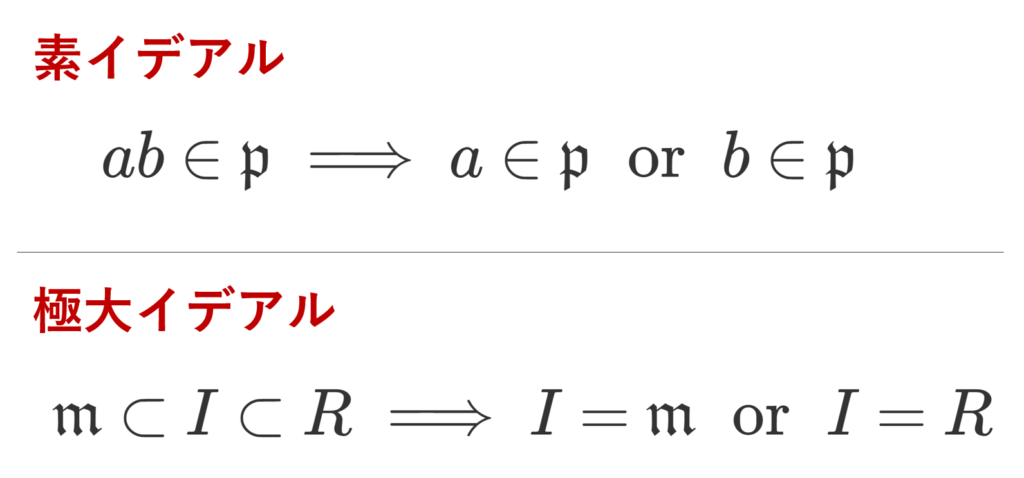
以上を踏まえて具体例を挙げましょう。
例1.
p が素数のとき,p の倍数の集合 p\mathbb{Z}\subset \mathbb{Z} は \mathbb{Z} の素イデアルである。また,p\mathbb{Z} は極大イデアルでもある。
一方で,整数 m\ge 2 が素数でないとき, m\mathbb{Z} は素イデアルでも極大イデアルでもない。
ab が p の倍数なら,a と b の少なくとも一方が p の倍数ですね。すなわち, ab\in p\mathbb{Z}\implies a\in p\mathbb{Z}\text{ or } b\in p\mathbb{Z} ですから, p\mathbb{Z} は素イデアルです。むしろ素イデアルは,素数の概念を一般化したものといえるでしょう。
また, \mathbb{Z}/p\mathbb{Z} は体になるので, p\mathbb{Z} は極大イデアルでもあります。
一方で,たとえば m=6 とすると, ab が 6 の倍数でも a,b の少なくとも一方が6の倍数とは言えませんね。 よって 6\mathbb{Z} は素イデアルではありません。また, 6\mathbb{Z}\subset 2\mathbb{Z} ですから, 6\mathbb{Z} は極大イデアルでもありませんね。
例2.
整数係数多項式環 \mathbb{Z}[x] に対し, (x) は素イデアルである。一方で, (x)\subset (x,2) なので, (x) は極大イデアルではない。
実数係数多項式環 \mathbb{R}[x] に対し, (x) は素イデアルであり,また \mathbb{R}[x] は単項イデアル整域(PID)なので,極大イデアルでもある。
fg\in (x) とすると, fg は x で割り切れますから, f,g を x で割った余りをそれぞれ r,s\in \mathbb{Z} とすると, rs=0 ですね。よって r=0 または s=0 ですね。したがって, f,g のいずれか一方は x で割り切れるので, f\in (x) または g\in (x) となり, (x) は素イデアルであることが分かります。
同様に, \mathbb{R}[x] においても (x) は素イデアルですが,体上の1変数多項式環は単項イデアル整域(PID)ですから,極大イデアルでもあります。
\mathbb{Z}[x] と \mathbb{R}[x] の大きな違いは,係数が体でないか,体であるかです。
極大イデアルの存在
最後に,クルルの定理 (Krull’s theorem) ともいわれる,極大イデアルの存在定理を紹介し,証明しておきましょう。
定理2(極大イデアルの存在)
R を可換環, I\subsetneq R をイデアルとする。このとき, I を含む極大イデアルが存在する。
この定理は,選択公理と同値な命題であるツォルンの補題を用います。選択公理がカギを握る定理です。
証明
\mathscr{I}_I =\{ I\subset J\subsetneq R \mid J\text{ is ideal}\}
を, I を含む真のイデアル全体の集合とする。 I\in \mathscr{I}_I より,\mathscr{I}_I は空でない。
\mathscr{I}_I は包含関係による半順序集合である。 \{J_\lambda\}\subset \mathscr{I}_I を全順序部分集合とする。このとき,
I_\infty = \bigcup_{\lambda} J_\lambda
はイデアルである。もし I_\infty=R なら,ある \lambda' があって 1\in I_{\lambda'} となり, I_{\lambda'} = R となって矛盾する。よって, I_\infty\neq R である。また, I\subset I_\infty である。したがって, I_\infty \in \mathscr{I}_I であり, \mathscr{I}_I は帰納的半順序集合である。
ツォルンの補題より, \mathscr{I}_I には極大元が存在する。
証明終