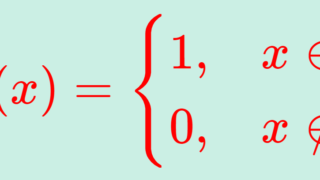高校や大学教養数学で学習する定積分はリーマン積分 (Riemann integral) と呼ばれ，リーマン和というものを用いて定義されます。これについて，その定義とリーマン積分可能な十分条件，リーマン積分不可能な関数の例について，順に述べましょう。
リーマン和による定積分の定義
定義（リーマン積分）
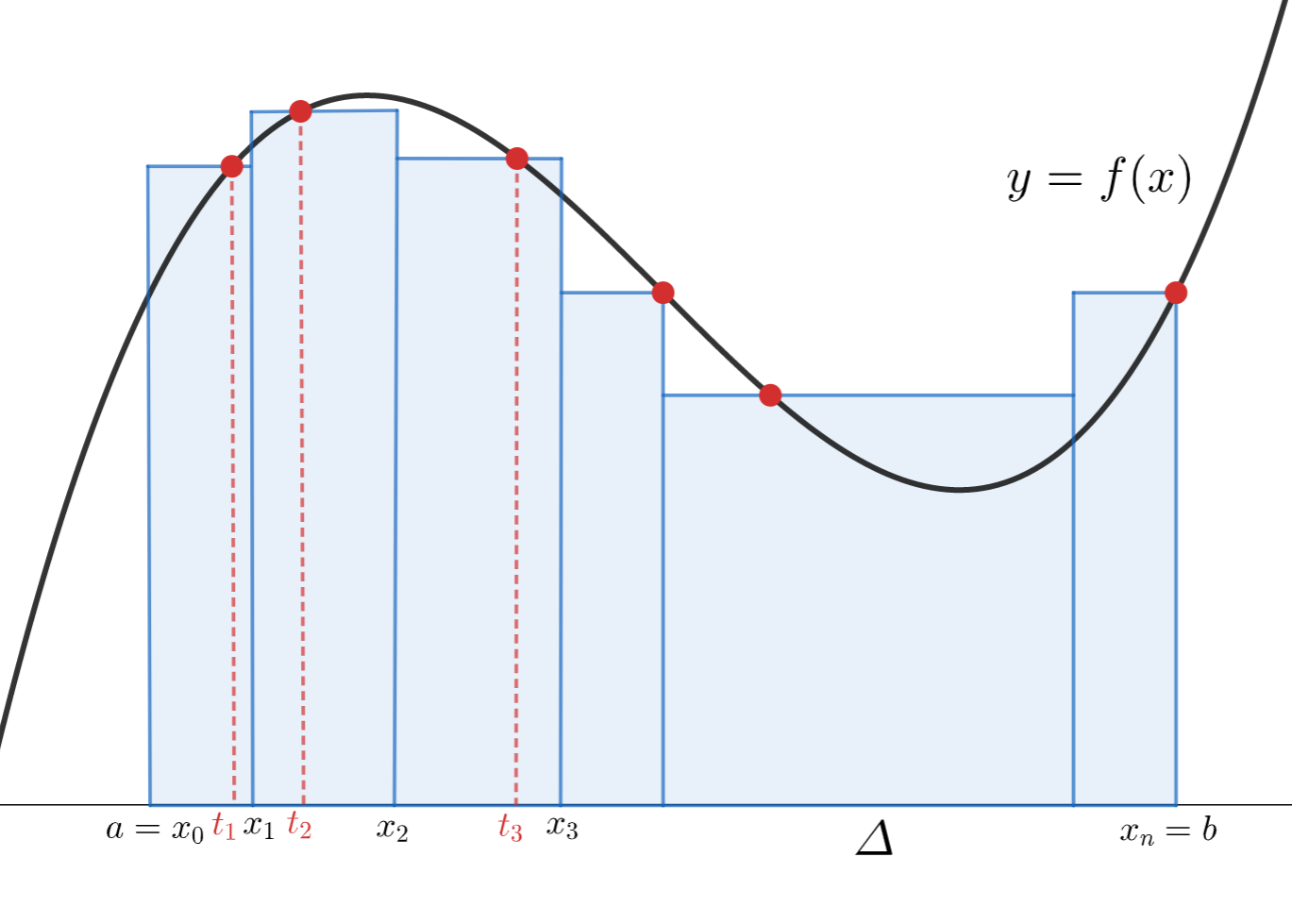
f \colon [a,b] \to \mathbb{R} を有界な関数とし，適当に a = x_0 < x_1 < x_2 < \dots < x_n = b とすることで，区間を分割する。
各区間の幅を \varDelta_k = x_k - x_{k-1} とし， t_k \in [x_{k-1}, x_k] を適当に選ぶ。このときの
\color{red} \sum_{k=1}^n f(t_k) \varDelta_k
を \{[x_{k-1}, x_k], t_k\} に関する f のリーマン和 (Riemann sum) という。
さらに，区間の幅を |\varDelta| = \max_{1\le k \le n} \varDelta_k と定め， |\varDelta| \to 0 となるように分割を変える(同時に n\to\infty となる)。このとき，分割および \{t_k\} の取り方に関係なく
\lim_{|\varDelta| \to 0 } \sum_{k=1}^n f(t_k) \varDelta_k
が存在するならば， f は [a,b] 上リーマン積分可能 (Riemann integrable) であるといい，この極限値を
と表し，これを f の [a,b] 間の定積分という。
ここで分割幅を |\varDelta |\to 0 とすると，分割数は n \to \infty となることに注意しましょう。 n は |\varDelta| と連動しています。
図で表現してみると，リーマン和とは以下の長方形の面積の合計になります。
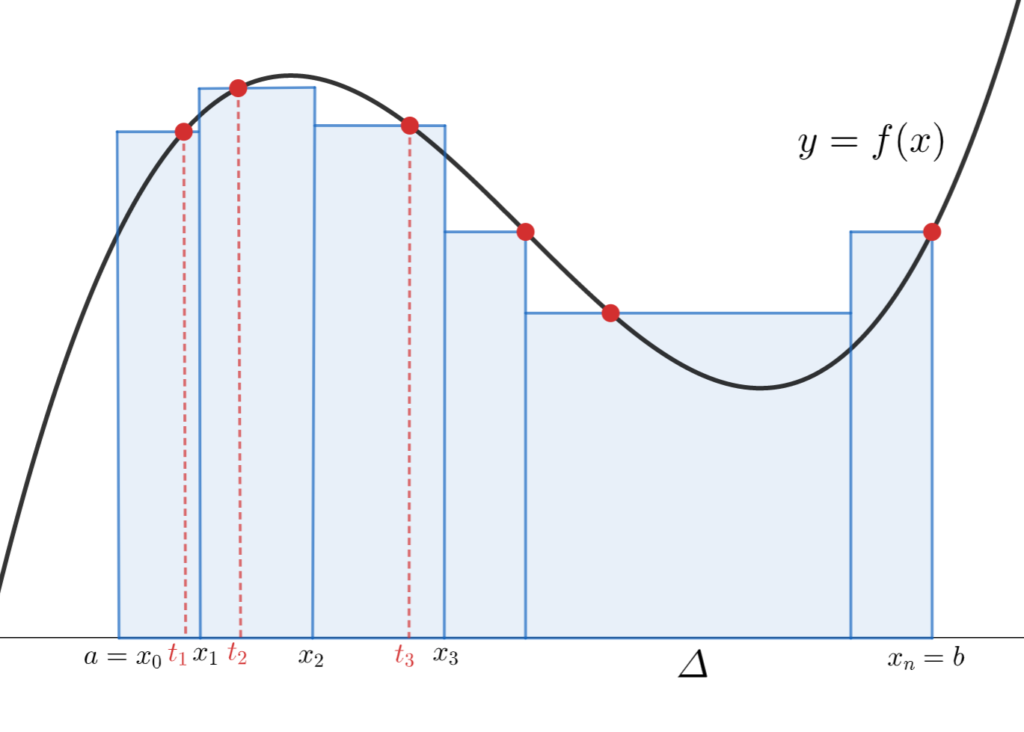
区間の分割をより細かくしてみましょう。
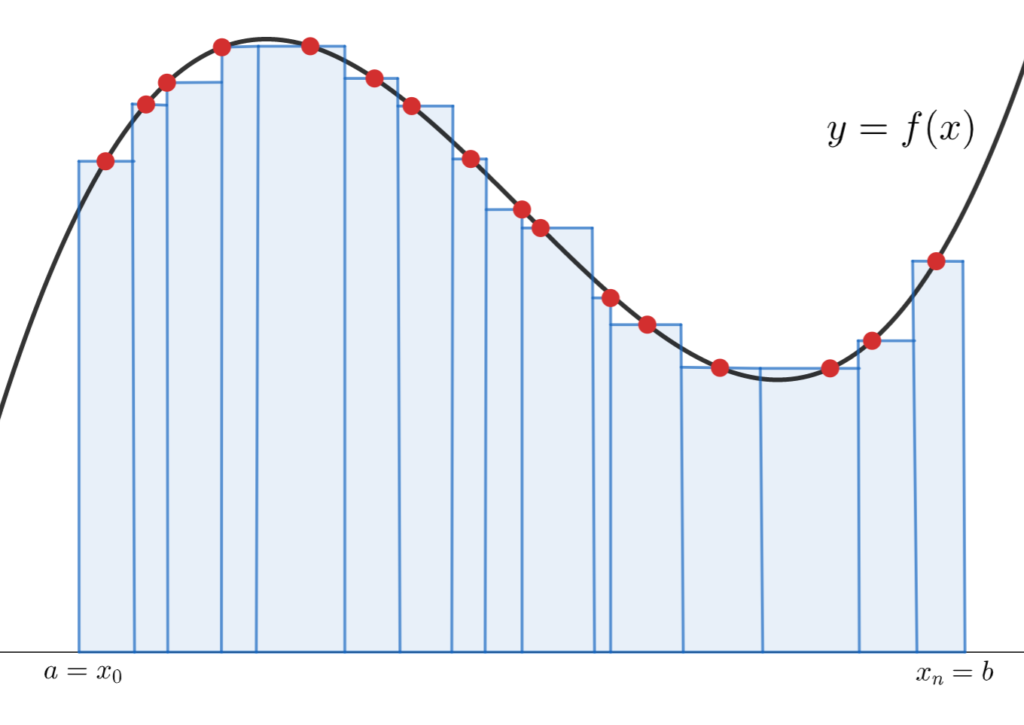
同じような理論でどんどん細かくしていけば，結局曲線と x 軸の間の面積に近似されていくのが分かるのではないでしょうか。
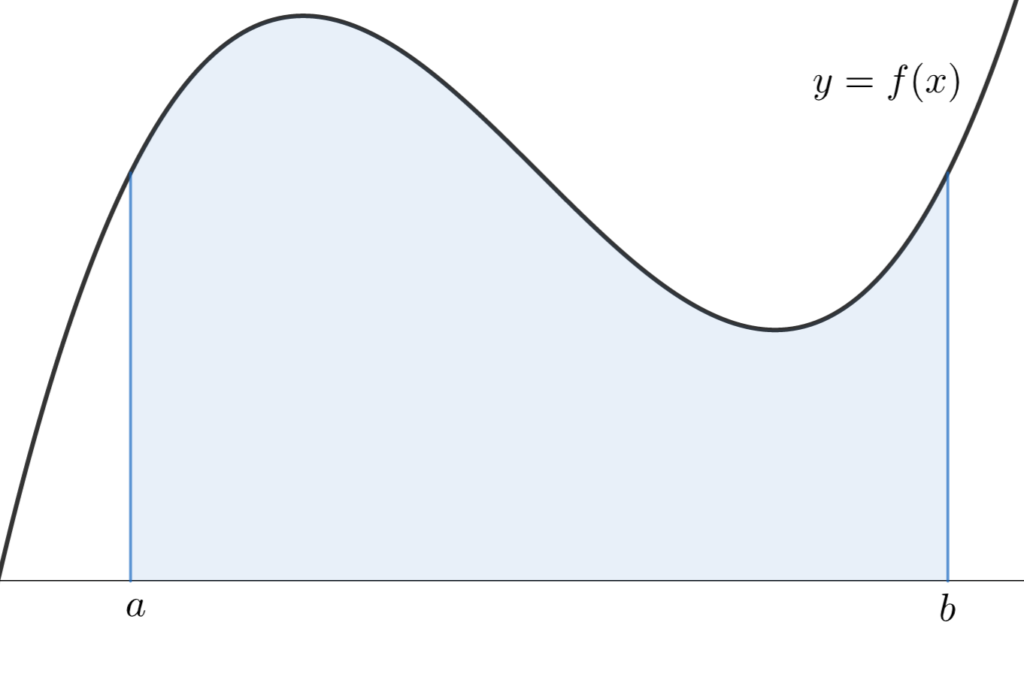
リーマン和とは，面積の長方形近似といえるわけですね。
リーマン積分可能な例とその証明
それでは，どういうときにリーマン積分可能なのでしょうか。これについて，十分条件を考えてみましょう。
単調あるいは連続な関数はリーマン積分可能
定理（リーマン積分可能な十分条件）
f\colon [a,b]\to \mathbb{R} とする。
- f が単調であるとき，リーマン積分可能である。
- f が連続であるとき，リーマン積分可能である。
高校生は，連続な関数しか定積分しないと思いますが，連続な関数は定積分できるからですね。
証明
証明
1. f が単調であるとき，リーマン積分可能である。
f を単調増加として示す。このとき，リーマン和について
\begin{aligned} &\sum_{k=1}^n f(x_{k-1}) \varDelta_k \\ &\le \sum_{k=1}^n f(t_k) \varDelta_k \\ &\le \sum_{k=1}^n f(x_k) \varDelta_k \\ \end{aligned}
である。 |\varDelta| \to 0 とすると，左辺は増加し右辺は減少することに注意。ここで右辺と左辺の差について，
であるため， \sum_{k=1}^n f(t_k) \varDelta_k は分割に依らず収束する。よってリーマン積分可能である。
2. f が連続であるとき，リーマン積分可能である。
f は有界閉区間 [a,b] 上連続なので，特にこの上で一様連続である(→有界閉区間上の連続関数は一様連続になることの証明)。
従って \varepsilon> 0 に対して，ある \delta> 0 が存在して，
|x- y | < \delta \implies |f(x) - f(y) | < \varepsilon
となる。ここで，
である。 |\varDelta| \to 0 とすると，左辺は増加し右辺は減少することに注意。ここで右辺と左辺の差について， |\varDelta| < \delta とすると
より分かった。
証明終
リーマン積分不可能な関数の例
リーマン積分不可能な関数の例
ディリクレ関数 \color{red} f(x) = 1_{\mathbb{Q} }(x) = \begin{cases} 1 & x \in \mathbb{Q}, \\ 0 & x\in \mathbb{R} \setminus \mathbb{Q} \end{cases} はリーマン積分不可能である。
実際，任意の区間には有理数も無理数も含まれているため，常に t_k\in \mathbb{Q} となるようにリーマン和を取ると，\sum_{k=1}^n f(t_k) \varDelta_k = \sum_{k=1}^n \varDelta_k =b-a となり，常に t_k \in \mathbb{R} \setminus \mathbb{Q} となるように取ると，\sum_{k=1}^n f(t_k) =0 となるため，同じ値に収束しません。よってリーマン積分不可能です。
ディリクレ関数について詳しくは，以下を参照してください．
1_{\mathbb{Q}} のような書き方は，定義関数（指示関数・特性関数）と呼ばれるものです。これについては，以下で詳しく解説しています。
原始関数が存在するとき，積分値は原始関数を用いてかける
次の定理は有名かつ重要です。
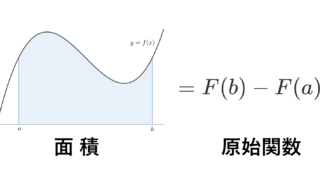
微分積分学の基本定理 (Fundamental theorem of calculus)
f\colon [a,b]\to \mathbb{R} が(リーマン)積分可能かつ原始関数 F を持つならば，
\color{red}\int_a^b f(x)\, dx = F(b)-F(a)
が成立する。
これについての証明は，以下の記事で解説しています。
