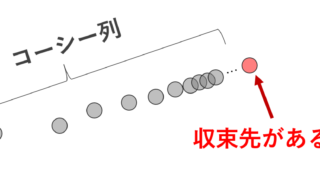
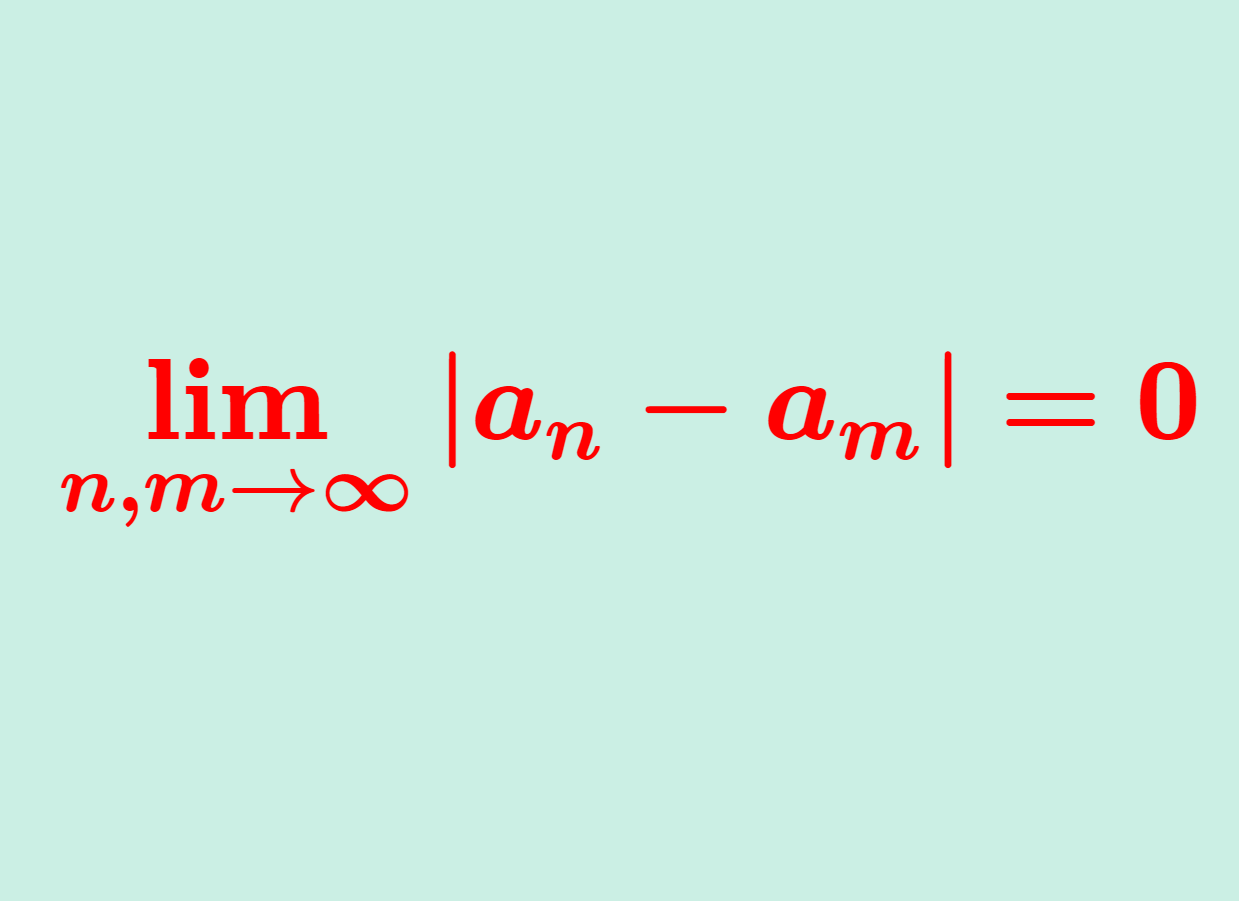コーシー列(基本列)は,大学1年生の微分積分学において,収束値は分からないが収束することが分かる,収束判定の道具といえます。これについて,定義と収束性の証明を行いましょう。
コーシー列の定義
定義(コーシー列)
実数または複素数の数列 \{a_n\} がコーシー列 (Cauchy sequence) または基本列 (fundamental sequence) であるとは,
任意の \boldsymbol{\varepsilon > 0} に対し,ある \boldsymbol{N \ge 1} が存在して,
\color{red} \boldsymbol{n, m \ge N \implies |a_n - a_m | < \varepsilon}
が成立することである。これは,
と書いても同じことを指す。
「任意の・ある~が存在する」なんて, \varepsilon\text{-}N 論法と同じ匂いがしますね(cf. イプシロンエヌ論法をわかりやすく丁寧に~数列の極限の定義~)。なお,∀(全称記号,任意の)と∃(存在記号,存在する)の使い方を知っていれば,
\forall \varepsilon>0, \exists N\ge 1,\, n,m \ge N \implies |a_n-a_m|<\varepsilon
ともかけます(本記事は分からなくても読めます)。
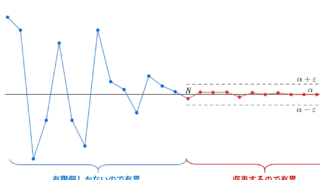
要は n,m をどんどん大きくしていけば,差 |a_n - a_m| はどんどん小さくなると言っています。
「差がどんどん小さくなる」とは,すなわち \{a_n \} の変動はどんどん消滅していくということを意味しており,そのような数列をコーシー列というわけです。
なお, \lim_{n,m\to\infty} と書いたときには, n,m はそれぞれ独立・自由に \infty に飛ばしていることに注意してください。
コーシー列 ⇔ 収束列
実数または複素数の数列がコーシー列であることと,収束列であることは同値であることが知られています。
コーシー列 ⇔ 収束列の定理の主張
定理(コーシー列と収束列は同値)
\{a_n\} を実数列または複素数列とする。このとき,
\{a_n\} が収束列 \iff \{a_n\} がコーシー列
これにより, \{a_n\} が収束することを判定するのには,コーシー列であるかどうかを調べればよいことが分かります。このことより,コーシー列のことをコーシーの(収束)判定条件ということもあります。
ただし,コーシー列であることが分かったところで,収束する「値」までは分からないことに注意しましょう。
なお, \mathbb{R} と同様に,複素数の集合 \mathbb{C} でも同様のことが成立します(証明はたとえば,実部と虚部に分ければ実数のときと同じです)。
コーシー列 ⇔ 収束列の証明
早速証明しましょう。前提知識として,以下の2つが必要です。
- 数列の極限の定義 (→イプシロンエヌ論法をわかりやすく丁寧に~数列の極限の定義~)
- 有界列は収束部分列を持つ (→ボルツァノ–ワイエルシュトラスの定理とその証明)
証明
収束列 \implies コーシー列について
\lim_{n\to\infty} a_n = \alpha とする。
\varepsilon > 0 とすると,ある N \ge 1 が存在して,
である。これから, n, m \ge N のとき
となるから, \{a_n \} はコーシー列である。
コーシー列 \implies 収束列について
まず,コーシー列は有界であることを示そう。 \varepsilon > 0 とすると,コーシー列の定義と三角不等式から,ある N \ge n が存在して,
n \ge N \implies |a_n| \le |a_N| + \varepsilon
となるため, M = \max\{|a_1|,\dots, |a_{N-1}|, |a_N|+\varepsilon \} とおけば, |a_n| \le M \,\, (n \ge 1) となる。これは有界を意味する。
以上で有界性が示せたから,ボルツァノ-ワイエルシュトラスの定理により,収束部分列 \{a_{n_k}\} が存在する。
\lim_{k\to\infty} a_{n_k} = \alpha としよう。すると,ある K \ge 1 が存在して,
となる。ここで, \widetilde{N} = \max\{ N, n_K\} おく。上のことと,コーシー列の定義により, n,n_k \ge \widetilde{N} に対して,
である。これは, \lim_{n\to\infty} a_n = \alpha を意味する。
証明終
証明の途中で,「コーシー列は有界」を示しましたが,本定理よりもちろん「収束列は有界」です。これについては,以下の記事でも解説していますから,参照してみてください。
コーシー列 ⇔ 収束列を使った証明の具体例
「証明において,コーシー列を示すことで収束列を示す」定理の具体例を挙げておきましょう。どれも「収束値はわからない」という点に注意してください。
これらはどれも,級数に対して,コーシー列を用いています。級数に対してコーシー列を用いる時は, \{S_n= \sum_{k=1}^n a_k \} がコーシー列となるので,
\begin{aligned} |S_n - S_m| &= \left|\sum_{k=m+1}^n a_k \right| \\ &= |a_{m+1} + a_{m+2} + \dots + a_{n}| \end{aligned}
について調べねばなりません。
コーシー列の否定
コーシー列でないことも述べておきましょう。否定を取るときのポイントは,「任意の~」と「ある~~が存在する」を入れ替え,不等号を逆にすることです。
命題(コーシー列の否定)
\{a_n\} がコーシー列でないとは,
ある \varepsilon > 0 が存在して,任意の N \ge 1 に対し,ある m,n \ge N が存在して, |a_n - a_m | \ge \varepsilon
が成立することである。
発展~より一般のコーシー列~
コーシー列は,より一般の空間(距離空間)で定義されます。しかし,一般には 「コーシー列 \implies 収束列」は成立しません。
コーシー列であることと,収束列であることが同値となる空間のことを完備 (complete) であるといいます。
たとえば,実数・複素数の空間は「完備」ですが,有理数の空間は「完備」ではありません。詳しくは,以下で解説しています。
「収束の基本的なこと」に関する他の話題
- イプシロンエヌ論法をわかりやすく丁寧に~数列の極限の定義~
- イプシロンデルタ論法をわかりやすく丁寧に~関数の極限の定義~
- 極限の性質6つの証明(一意性,和,積,商,大小関係)
- 収束する数列は有界であることの証明
- はさみうちの原理とその厳密な証明~数列版・関数版~
- 追い出しの原理とその厳密な証明~数列版・関数版~
- 上に有界な単調増加数列は収束することの証明
- 実数上関数の収束と数列の収束の同値性とその証明
- ボルツァノ–ワイエルシュトラスの定理とその証明
- 【チェザロ平均】数列が収束するとき平均も同じ値に収束する証明
あいまい検索
級数におけるコーシーの収束判定法 (Cauchy’s root test) とは全くの別物です。これについては,以下の記事を参照してください。