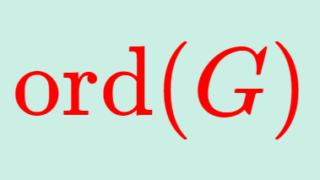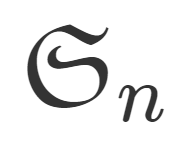巡回群とは,唯一つの元で生成される群を指します。巡回群について,その定義と例・性質4つを順番に紹介しましょう。
巡回群の定義
定義(巡回群)
G を群とする。 G が巡回群 (cyclic group) であるとは, G が唯一つの元で生成されることをいう。すなわち,ある g\in G が存在して, \color{red} G = \langle g\rangle とかけることをいう。
群の生成については,群の生成とは~定義と具体例~で解説しています。要は巡回群とは,すべての元が整数 a を用いて, g^a の形でかける群を指します。
有限群(位数が有限の群,すなわち有限集合の群)であるときは,生成元をスタートして,グルグル巡回しているイメージです。
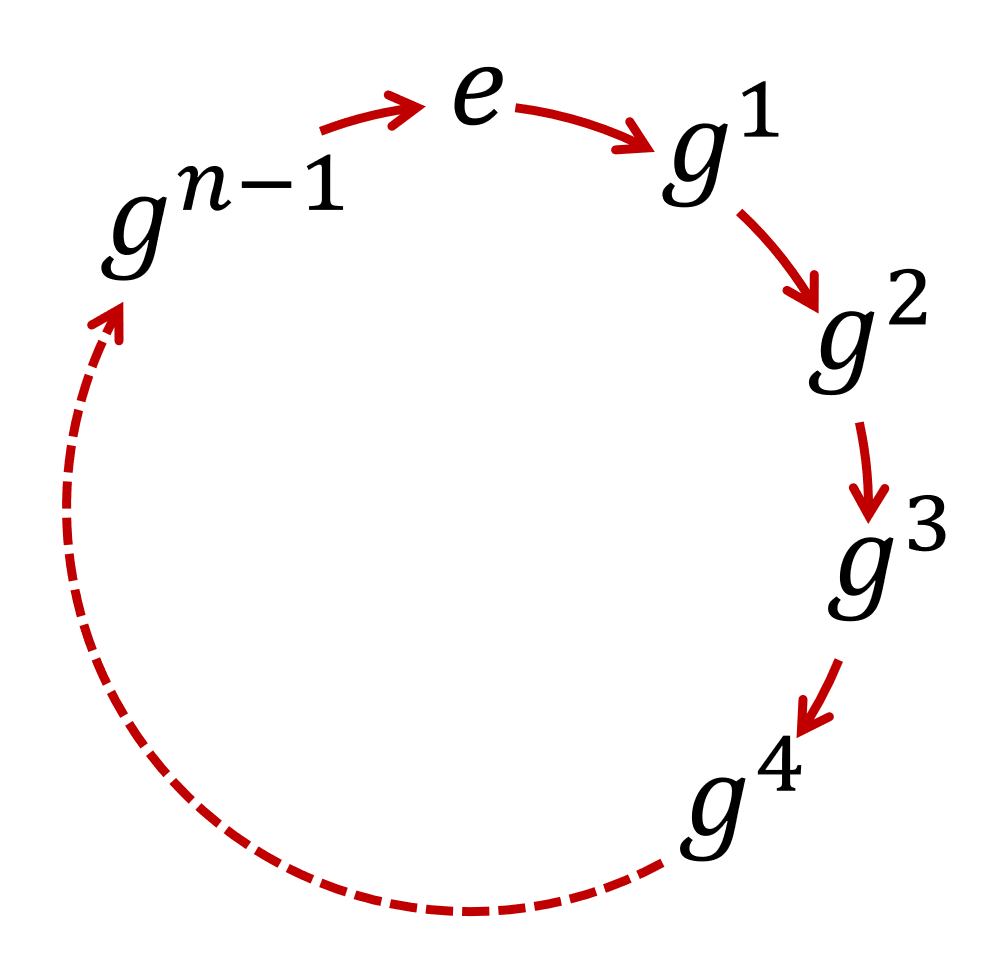
G が無限群(位数が無限の群,すなわち無限集合の群)であるとき,実際にグルグル巡回しているわけではありません。これを,無限巡回群といいます。
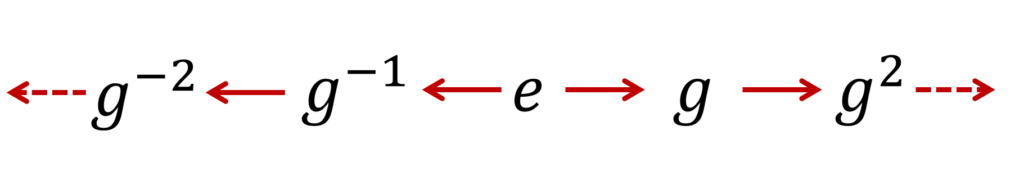
巡回群 G は,集合として高々可算集合です。
巡回群の具体例4つ
具体例を見ていきましょう。
例1.
m\ge 2 を整数とする。和(加法)に関する群 \mathbb{Z}/m\mathbb{Z} は 1 を生成元とする位数 m の巡回群である。
\mathbb{Z}/m\mathbb{Z} は{}\bmod m の世界です。 \mathbb{Z}/m\mathbb{Z}=\{0,1,2,\dots, m-1\} と考え, 1 で生成されますね。
例2.
和(加法)に関する群 \mathbb{Z} は 1 を生成元とする無限巡回群である。
任意の正の整数 n は n= 1+1+\dots + 1 と表せますし,負の整数も n = -1-1-\dots -1 と表せます。
例3.
積(乗法)に関する群 \{ e^{in\pi/6}\mid n\in\mathbb{Z}\} は e^{i\pi/6} を生成元とする位数 12 の巡回群である。
例4.
\sigma \colon \{1,2,\dots, m\} \to \{1,2,\dots, m\} を \sigma(k) = \begin{cases} k+1 & 1\le k\le m-1, \\ 1 &k=m\end{cases} と定める。写像の合成に関する群 \{1, \sigma, \sigma^2, \dots, \sigma^{m-1}\} は \sigma を生成元とする位数 m の巡回群である。
\sigma^m とは \sigma の m 回合成を表します。 巡回置換です。
巡回群の性質
さて,巡回群の性質を紹介します。
定理1(巡回群の性質)
G を巡回群とする。
- G の位数が n であるとき, G \simeq \mathbb{Z}/n\mathbb{Z} .
- G が無限群であるとき, G\simeq \mathbb{Z}.
巡回群 G の性質を調べたければ \mathbb{Z}/n\mathbb{Z} や \mathbb{Z} の性質をみればよいというわけです。
たとえば,巡回群 G は可換群(アーベル群)ですが,これは \mathbb{Z}/n\mathbb{Z}, \mathbb{Z} がそうだからです。他にも,巡回群の部分群は巡回群であることが分かります。
証明
巡回群 G の位数を n とすると,生成元を g として G=\{g^0, g^1, g^2, \dots, g^{n-1}\} とかける。このとき, f\colon G\ni g^m \mapsto m\in\mathbb{Z}/n\mathbb{Z} は明らかに同型写像である。よって, G \simeq \mathbb{Z}/n\mathbb{Z} .
巡回群 G の位数を \infty とすると,生成元を g として G=\{\ldots, g^{-2}, g^{-1}, g^0, g^1, g^2,\ldots \} とかける。このとき, f\colon G\in m \mapsto m \in\mathbb{Z} は明らかに同型写像である。よって, G\simeq \mathbb{Z}.
証明終
群 \{ e,g, g^2, \dots, g^{n-1}\} の指数部分のみに注目して, \{0,1,2,\dots, n-1\} を和に関する群と思ったものに同型というわけですね。
また,次のようなことも言えます。
定理2(巡回群となる群)
- 自明でない任意の群は,自明でない巡回群を部分群として含む。
- 素数位数の群は巡回群である。
「自明でない」とは,単位元のみからなる群 \{e\} ではないことを指します。
証明
1. 自明でない任意の群は,自明でない巡回群を部分群として含むこと
G を群とする。 g\in G を単位元でないとすると, \langle g \rangle \subset G は部分群である(→群の生成とは~定義と具体例~)。
2. 素数位数の群は巡回群であること
p を素数, G を位数 p の群とする。g\in G を単位元でないとすると,上と同じ議論で \langle g \rangle \subset G は部分群である。
ラグランジュの定理より,部分群の位数は p の約数であるから, \langle g \rangle の位数は p である。従って, \langle g\rangle = G であり, G は巡回群である。
証明終