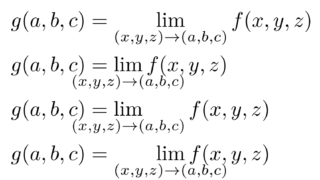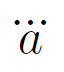【LaTeX】定義済み関数(max,lim,exp,log,sin等)38個一覧

$LaTeXにおける数学関数一覧(sinhの図)$ LaTeX

2021.04.182025.01.13

テクノロジー

記事内に広告が含まれている場合があります

$\LaTeX$ における，既に定義された関数38個を挙げましょう。

なお，amsmath パッケージの使用は仮定しています。

目次

定義済みの数学関数38個一覧
1. log 型関数22個
2. lim 型関数16個
mod に関するコマンド
上にない関数は自作しよう
その他のLaTeXコマンドまとめ記事
参考

定義済みの数学関数38個一覧

一覧を述べる前に，一つだけ大切な概念を説明します。数学関数にはlog型とlim型があります。

log型とは，\log_x f とすると，

\color{red} \log_x f

のように添え字が右下につく関数，より一般に \ope_a^b f とすると， $\displaystyle \color{red} \operatorname{ope}_a^b f$ のような添え字の付き方をする関数を指します。

lim型とは，\lim_{x \to 0} f(x) とすると，

\color{red} \lim_{x\to 0} f(x)

のように添え字が真下につく関数，より一般に \ope_a^b f とすると， $\displaystyle \color{red} \operatorname*{ope}_a^b f$ のような添え字の付き方をする関数を指します(ただしディスプレイスタイルに限る)。

このそれぞれについて，定義済みの関数をまとめます。

log 型関数22個

関数など	コマンド	主な意味
$\sin$	`\sin`	サイン，正弦(三角関数)
$\cos$	`\cos`	コサイン，余弦(三角関数)
$\tan$	`\tan`	タンジェント，正接(三角関数)
$\arcsin$	`\arcsin`	アークサイン，逆正弦(逆三角関数)
$\arccos$	`\arccos`	アークコサイン，逆余弦(逆三角関数)
$\arctan$	`\arctan`	アークタンジェント，逆正接(逆三角関数)
$\sec$	`\sec`	セカント，正割(三角関数)
$\csc$	`\csc`	コセカント，余割(三角関数)
$\cot$	`\cot`	コタンジェント，余接(三角関数)
$\sinh$	`\sinh`	ハイパボリックサイン，双曲線正弦(双曲線関数)
$\cosh$	`\cosh`	ハイパボリックコサイン，双曲線余弦(双曲線関数)
$\tanh$	`\tanh`	ハイパボリックタンジェント，双曲線正接(双曲線関数)
$\coth$	`\coth`	ハイパボリックコタンジェント，双曲線余接(双曲線関数)
$\exp$	`\exp`	指数，exponential $\exp x = e^x$
$\log$	`\log`	対数
$\ln$	`\ln`	自然対数 $\log_e$
$\lg$	`\lg`	常用対数 $\log_{10}$ ・2進対数 $\log_2$
$\arg$	`\arg`	偏角，argument
$\deg$	`\deg`	(多項式などの)次数，degree
$\dim$	`\dim`	(ベクトル空間などの)次元，dimension
$\ker$	`\ker`	(線形写像などの)核，kernel
$\hom$	`\hom`

lim 型関数16個

関数など	コマンド	主な意味
$\max$	`\max`	最大値
$\min$	`\min`	最小値
$\sup$	`\sup`	上限
$\inf$	`\inf`	下限
$\lim$	`\lim`	極限
$\limsup$	`\limsup`	上極限
$\varlimsup$	`\varlimsup`	上極限
$\liminf$	`\liminf`	下極限
$\varliminf$	`\varliminf`	下極限
$\injlim$	`\injlim`	帰納極限
$\varinjlim$	`\varinjlim`	帰納極限
$\projlim$	`\projlim`	射影極限
$\varprojlim$	`\varprojlim`	射影極限
$\det$	`\det`	行列式，determinant
$\gcd$	`\gcd`	最大公約数
$\Pr$	`\Pr`	確率

$\lim$ などのテクニックは，以下も参照してください。

mod に関するコマンド

$\bmod$ は他の数学関数に比べて，少し特殊です。これについては，以下の記事で解説しています。

上にない関数は自作しよう

上で述べた以外の数学関数が使いたいこともあるでしょう。そういうときは，自分で作るとよいです。これは，\DeclareMathOperator を使えばできます。これについては以下で解説しています。

その他のLaTeXコマンドまとめ記事

参考

amsmath – AMS mathematical facilities for LAT

タイトルとURLをコピーしました