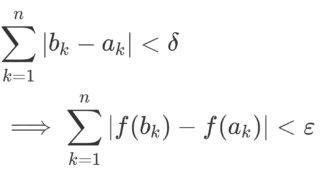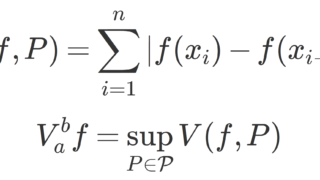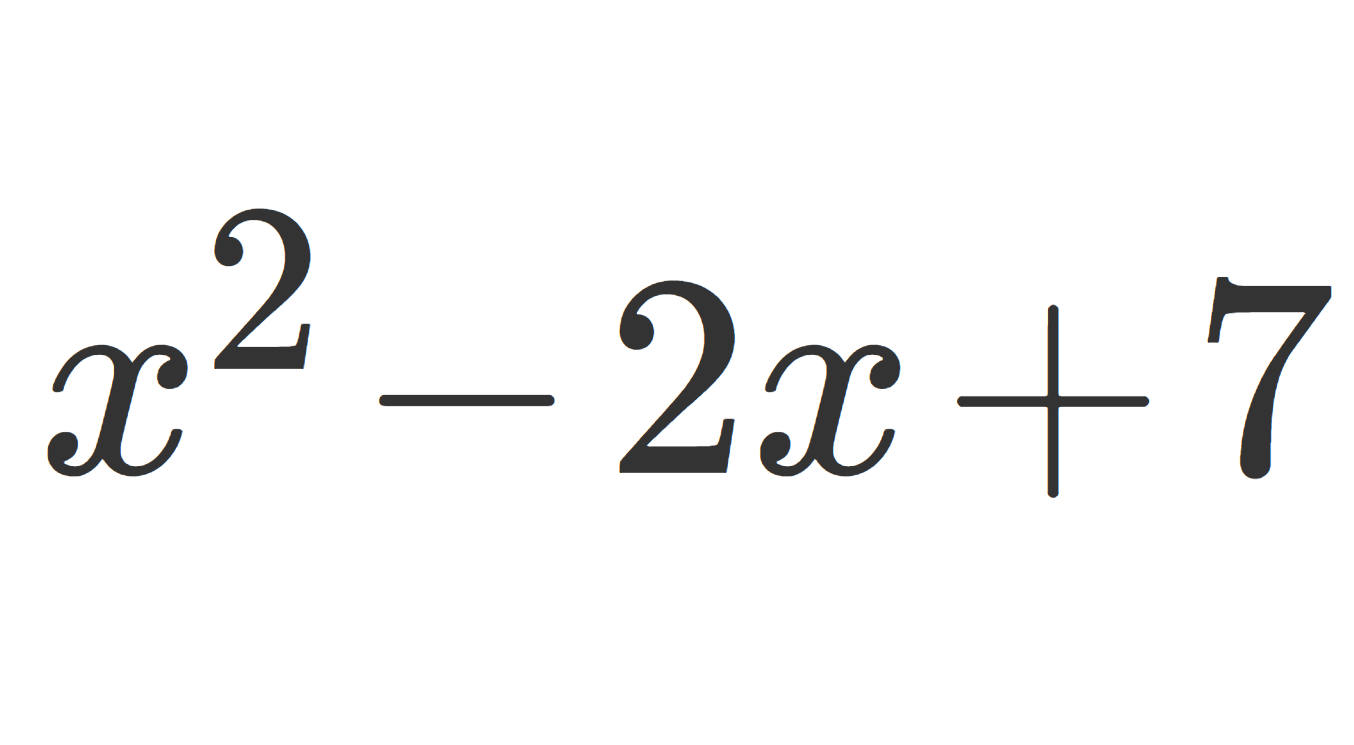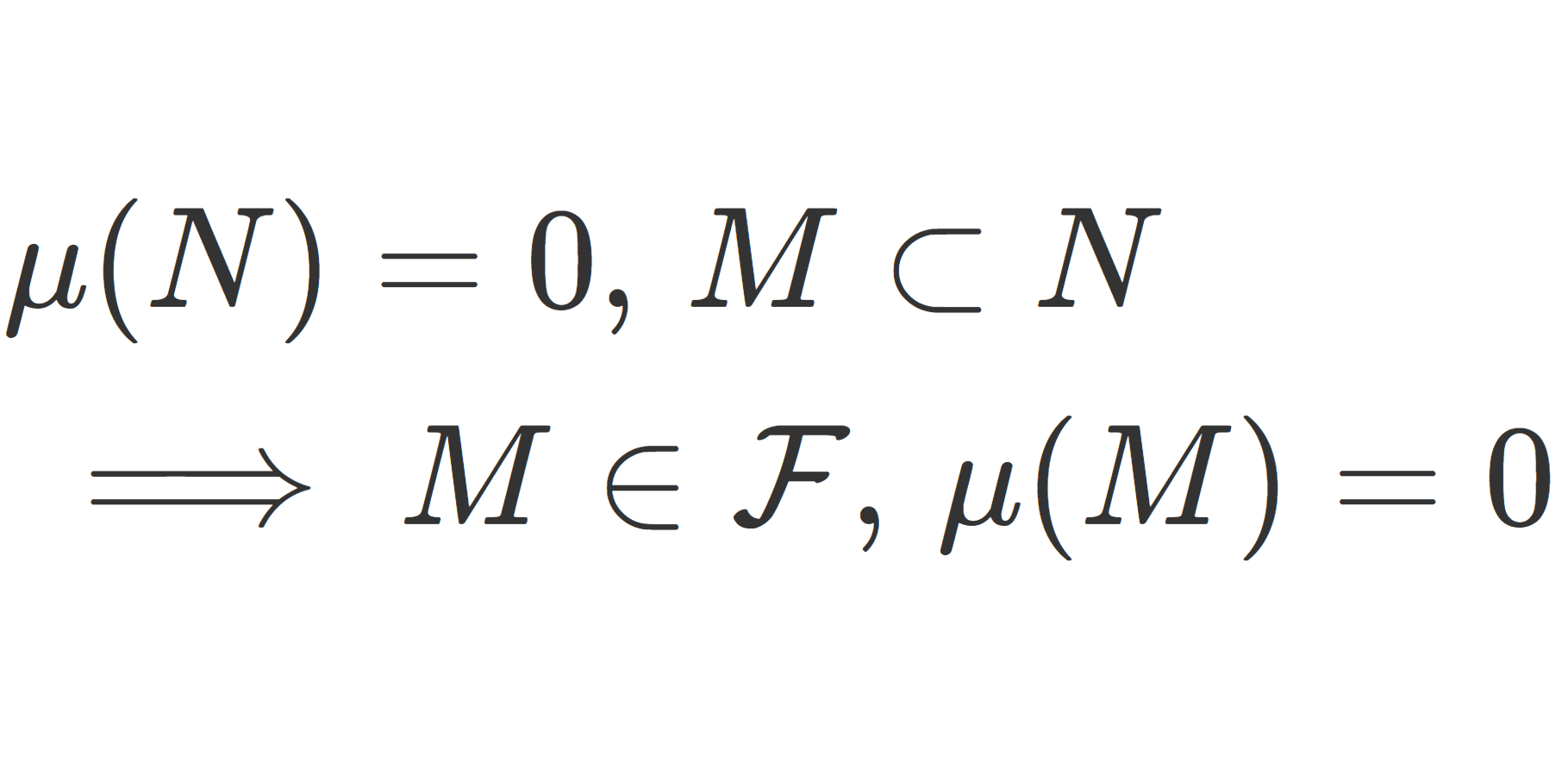関数 f がリプシッツ連続であるとは, |f(x)-f(y)|\le K|x-y| が成り立つことを指します。
リプシッツ連続について,その定義と例,一様連続など他の連続性との関係,微分と関連する性質について述べましょう。
リプシッツ連続と他の連続性との関係
リプシッツ連続の定義と,他の連続性との関係を見ていきましょう。
リプシッツ連続の定義
定義(リプシッツ連続)
関数 f\colon \R\to\R が,ある K>0 が存在して,
\large \color{red}|f(x)-f(y)|\le K|x-y|,\quad x,y\in \R
をみたすとき,リプシッツ連続 (Lipschitz continuous) であるという。より一般に,距離空間 X,Y において,関数 f\colon X\to Y が
をみたすとき,リプシッツ連続 (Lipschitz continuous) であるという。
x\ne y のとき,一つ目の赤字の式は,
\left|\frac{f(x)-f(y)}{x-y}\right|\le K
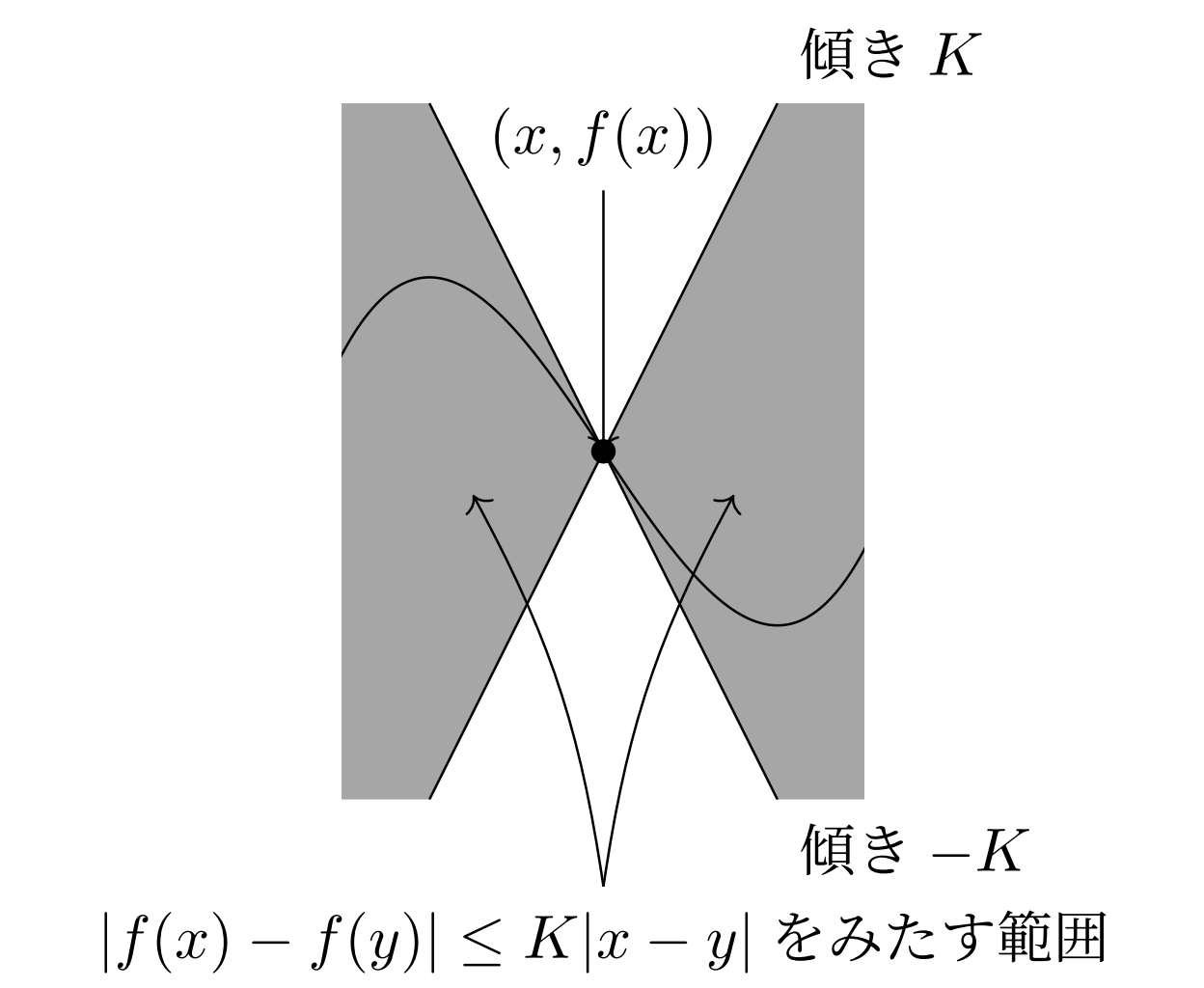
とかいても同じですね。平均変化率が有界だということです。図にすると以下のように,グラフ上の任意の点 (x,f(x)) から傾き \pm K の直線を引いたときに,グラフは常にその直線の間の部分に入る,ということを意味します。
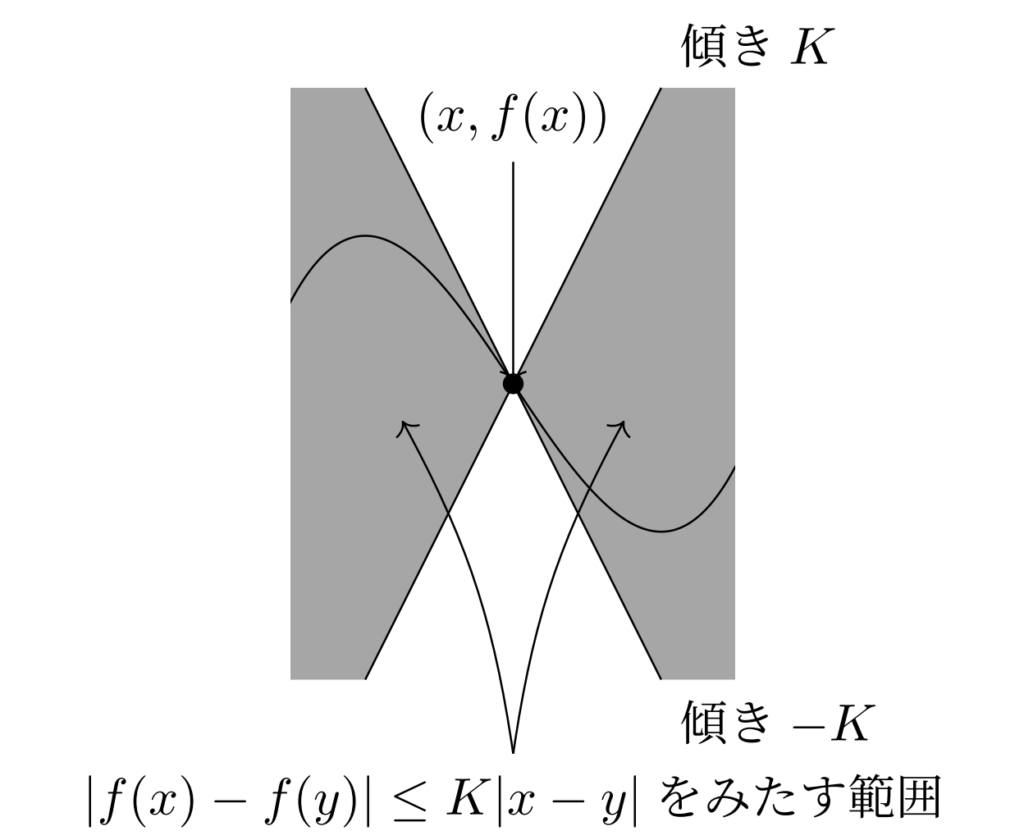
なお,リプシッツ連続の定義において K<1 のとき, f を縮小写像 (contraction mapping) といいます。縮小写像には,バナッハの不動点定理(縮小写像の原理)が有名です。バナッハの不動点定理(縮小写像の原理)とその証明で解説しています。
リプシッツ連続は,微分方程式の解の初期値問題で,解の一意性を保証するのに出てくる条件(リプシッツ条件といいます)でもあります。
他の連続性との関係
関数には,リプシッツ連続以外に様々な連続性の概念があります。それをまとめておきましょう。
| 用語 | 数式 |
|---|---|
| リプシッツ連続 | |f(x)-f(y)|\le K|x-y| |
| \alpha-ヘルダー連続 | |f(x)-f(y)|\le K|x-y|^\alpha |
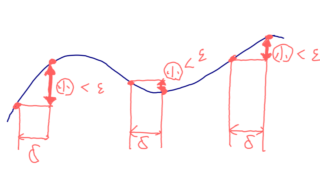
| 絶対連続 | \displaystyle \sum_{k=1}^n|x_{k}-y_{k}|<\delta \implies \sum_{k=1}^n |f(x_k)-f(y_{k})|<\varepsilon |
| 一様連続 | |x-y|<\delta \implies |f(x)-f(y)|<\varepsilon |
| 有界変動 | \displaystyle \sup_{P\in\mathcal{P}}\sum_{k=1}^n |f(x_{k})-f(x_{k-1})|<\infty |
一般に,関数 f\colon \textcolor{red}{\boldsymbol{[a,b]}}\to \R について,以下のような包含関係が成立します。
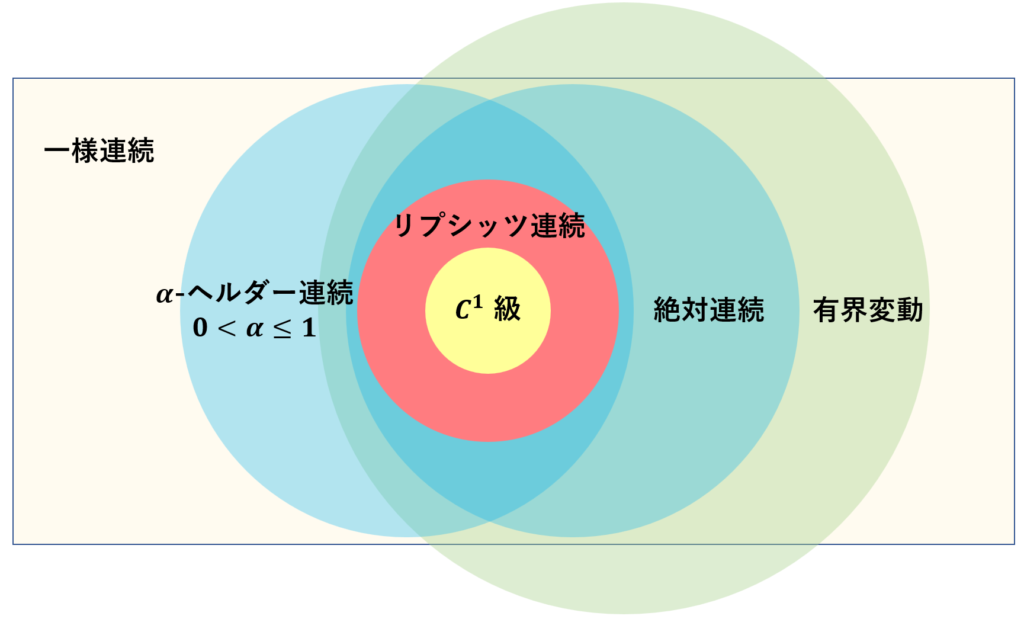
リプシッツ連続関数は絶対連続ですから,特に,リプシッツ連続関数はほとんどいたるところ微分可能です。
リプシッツ連続関数の例・そうでない例
例1.
f(x)=|x| ,\; (x\in\R) はリプシッツ連続である。
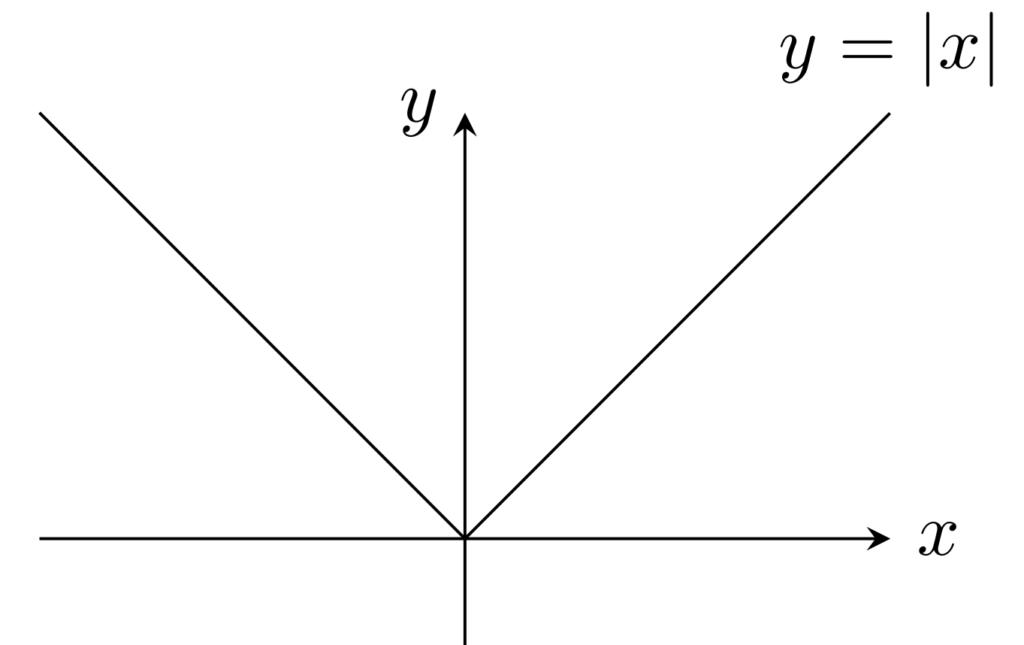
|f(x)-f(y)|=\bigl||x|-|y|\bigr|\le |x-y| なので明らかですね。
例2.
f(x)=\sin x はリプシッツ連続である。
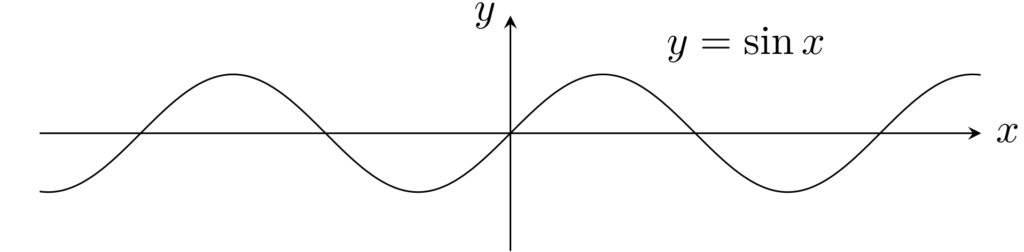
|\sin x- \sin y|\le |x-y| なので明らかですね。
例3.
f(x)=x^2 \; (-1\le x\le 1) はリプシッツ連続だが, f(x)=x^2\; (x\in \R) はリプシッツ連続でない。一様連続でもない。
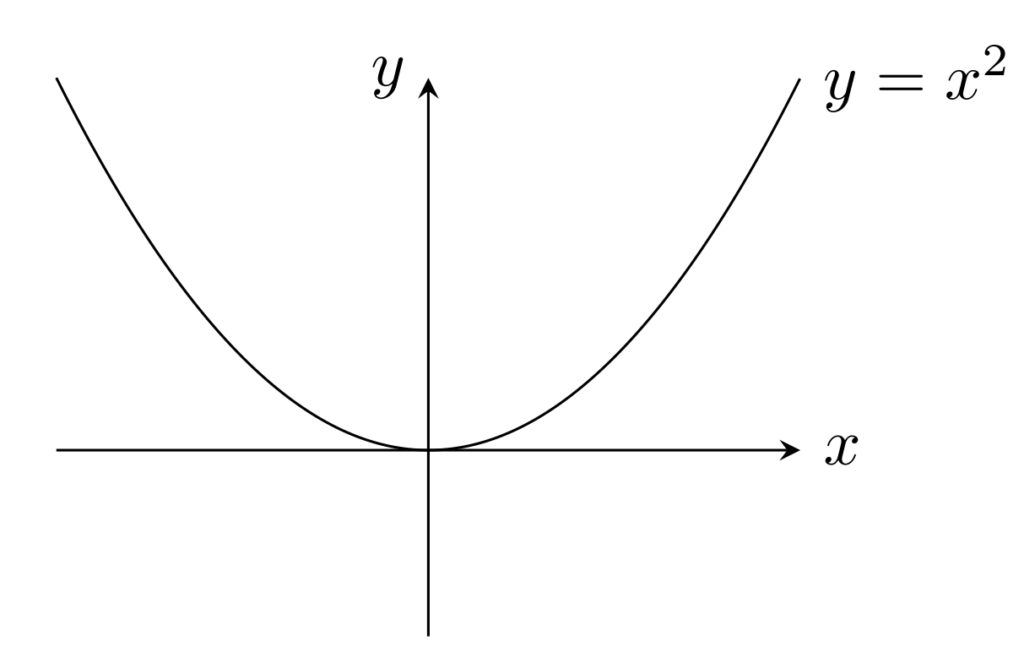
任意の x,y\in [-1,1] に対して |x^2-y^2|\le 2|x-y| なので,定義域を [-1,1] とすればリプシッツ連続ですが,
\frac{(x+1)^2-x^2}{(x+1)-x} \xrightarrow{x\to\infty}\infty
のため, |(x+1)^2-x^2|\le K|(x+1)-x| となる x \in\R によらない定数 K は存在しません。よって,定義域を \R とした場合はリプシッツ連続ではありません。
例4.
f(x)=\sqrt{x}\; (x\ge 0) は一様連続・絶対連続だが,リプシッツ連続ではない。
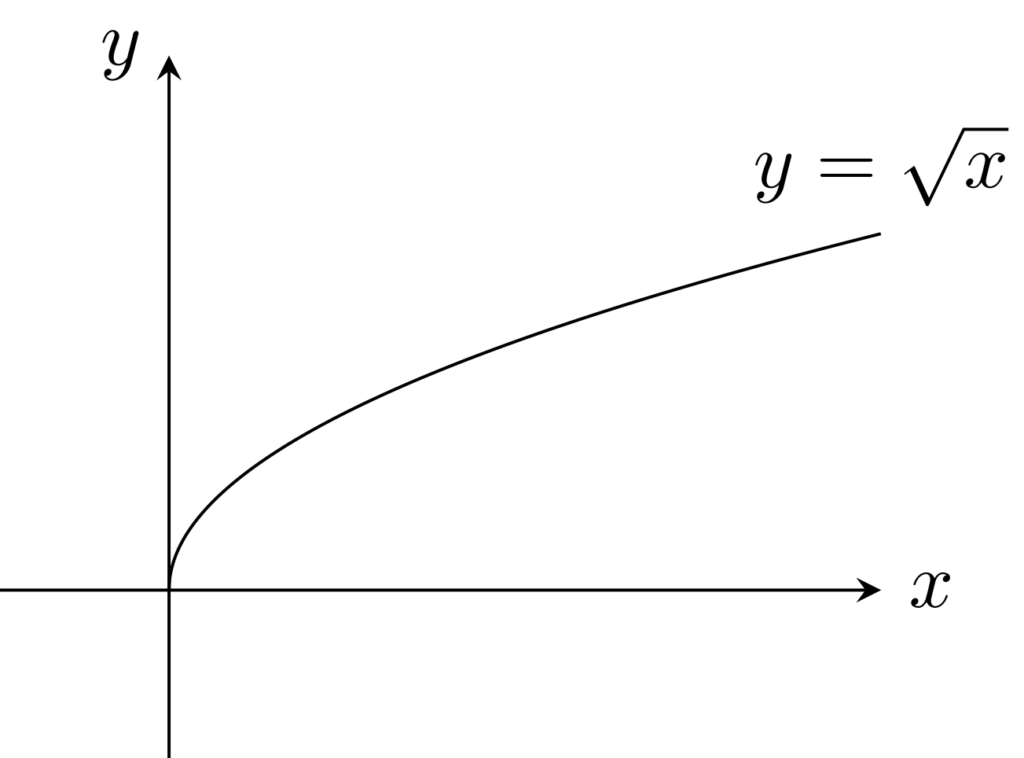
リプシッツ連続でないことは,
\left|\frac{f(x)-f(0)}{x-0}\right|= \frac{1}{\sqrt{x}}\xrightarrow{x\to 0+} \infty
よりよいです。一方で,\varepsilon >0 に対し,互いに素な区間列 \{ (x_k, y_k)\} が \sum_{k=1}^n |y_k-x_k|<\varepsilon^2 をみたすとすると,
となるため,絶対連続ですね。
なお,一様連続だが絶対連続でない例は絶対連続な関数とは~定義と例と性質4つ~で解説しています。
リプシッツ連続関数の性質
証明
\implies は,リプシッツ連続の定義から,
\left| \frac{f(x)-f(y)}{x-y}\right|\le K
で,両辺 y\to x とすることで |f'(x)|\le K となるからよい。
\impliedby は,平均値の定理より, x<y に対し,ある x<c<y が存在して,
\left| \frac{f(x)-f(y)}{x-y}\right| =|f'(c)|\le K
となるからよい。
証明終
定理2は定理1と似ていますが,少し違います。
定理2(リプシッツ連続関数と絶対連続)
I\subset \R とし, f \colon I\to\R は絶対連続であるとする(したがってほとんどいたるところ微分可能である)。このとき,
f がリプシッツ連続\iff f' が有界
である。
ここで f' が有界とは, |f'(x)|\le K, \,\text{a.e.\, }x\in\R ということです。
証明
\implies の証明は定理1.と全く同じである。
\impliedby について, f は絶対連続のため,ほとんどいたるところ微分可能で, x,y\in \R に対し,
\begin{align}f(x)-f(y)=\int_y^x f'(t)\, dt \end{align}
が成り立つ(→絶対連続な関数とは~定義と例と性質4つ~)。ここで, |f'|\le K より,
となって示せた。
証明終
定理2の \impliedby の証明では,平均値の定理は使えないし,逆に定理1の \impliedby の証明では,上式 (1) は使えません。