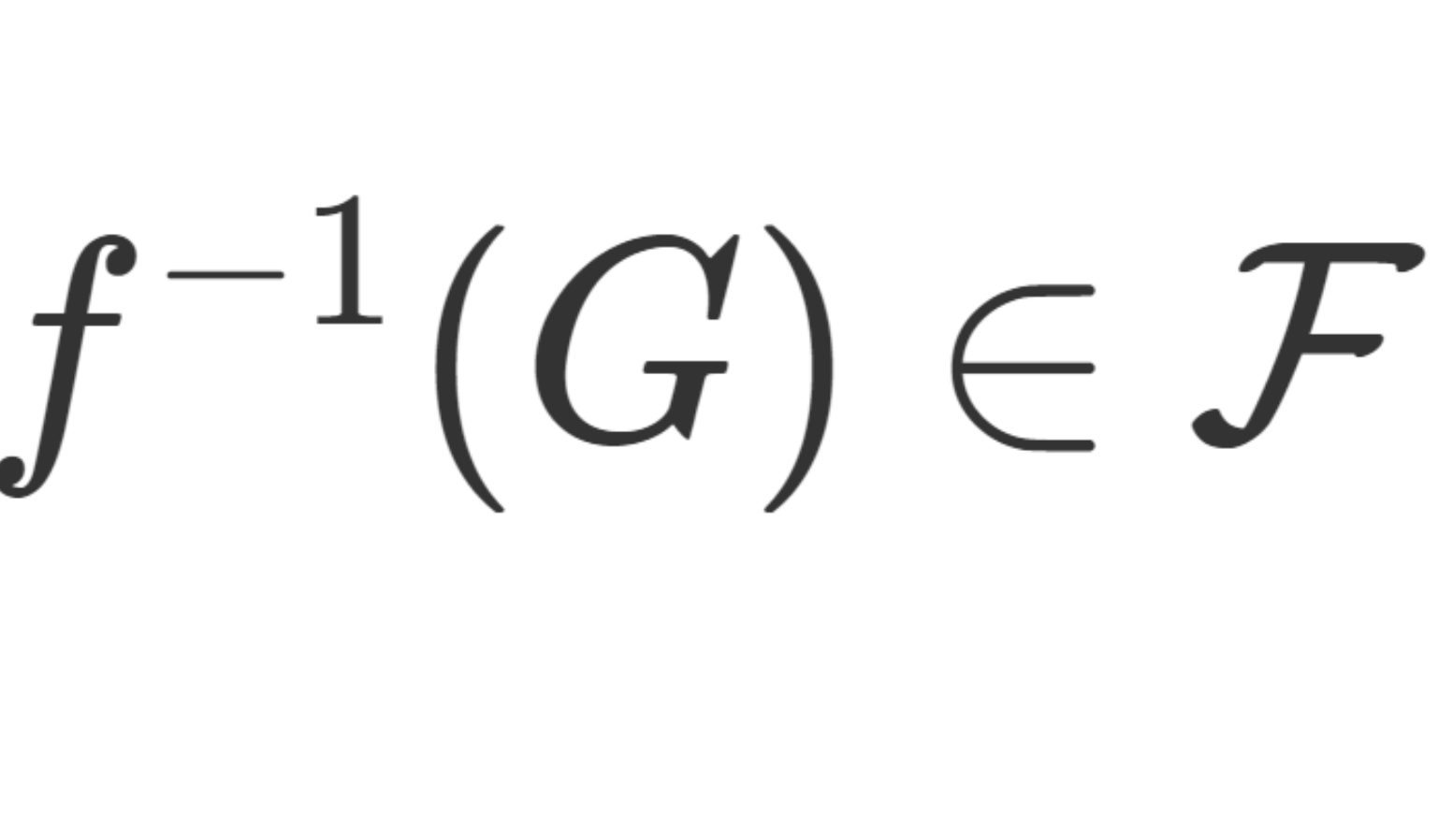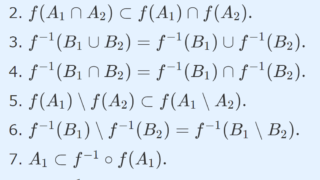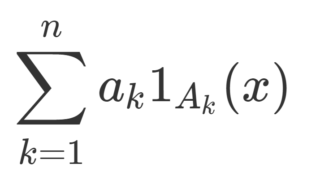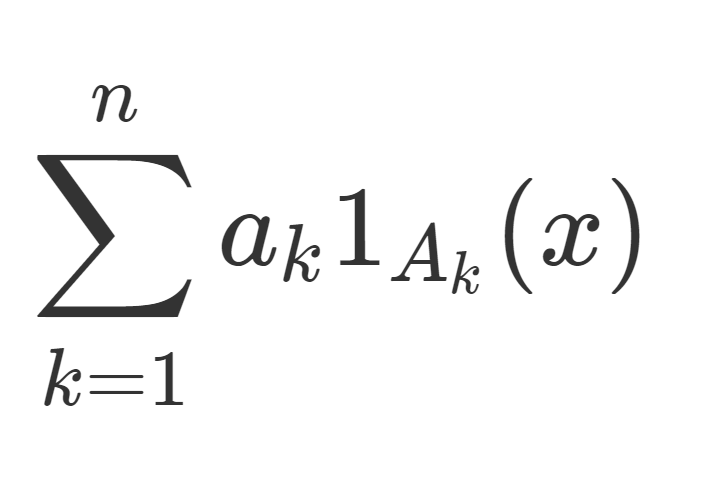可測関数(可測写像)とは,可測空間の間に定義されるいわゆる「構造を保つ関数」のことをいい,ルベーグ積分を考えることのできる大事な関数です。
可測関数の定義を行い,マスターすべき大事な性質を一気に紹介・証明しましょう。
可測関数の定義と性質

可測関数の定義
定義(可測関数)
(X,\mathcal{F}), (Y, \mathcal{G}) を可測空間とする。 f\colon X\to Y が可測関数(可測写像; measurable function) であるとは,
\large \color{red} G\in\mathcal{G} \implies f^{-1} (G) \in \mathcal{F}
が成立することを言う。 f^{-1} は f の逆像を表す。 X,Y が位相空間であり, \mathcal{F},\mathcal{G} がボレル集合族であるとき,可測関数 f はボレル可測 (Borel measurable) ともいう。
逆像を用いて定義するのは,位相空間における連続関数の定義のときと同じですね(→位相空間における連続写像の定義と性質を詳しく)。というのも,逆像は非常に性質が良いからです。具体的には,以下の性質がありました。
f\colon X\to Y を写像とするとき,
- f^{-1}(\emptyset) = \emptyset
- f^{-1}(A^c) = f^{-1}(A)^c
- f^{-1}(\bigcup_{\lambda\in\Lambda} A_\lambda)=\bigcup_{\lambda\in\Lambda}f^{-1} (A_\lambda)
- f^{-1}(\bigcap_{\lambda\in\Lambda} A_\lambda)=\bigcap_{\lambda\in\Lambda}f^{-1} (A_\lambda)
これに関連する話は以下の記事で行っています。
なお,定義からほぼ明らかですが,可測関数の合成もまた可測関数です。すなわち (X,\mathcal{F}),(Y,\mathcal{G}),(Z,\mathcal{H}) をそれぞれ可測空間, f\colon X\to Y,\, g\colon Y\to Z を可測関数とするとき, g\circ f\colon X\to Z も可測関数です。
σ加法族の生成と可測関数
定理1(σ-加法族の生成と可測関数)
(X,\mathcal{F}), (Y, \mathcal{G}) を可測空間とし, \sigma(\mathcal{C})=\mathcal{G} とする。 f\colon X\to Y が
\large \color{red} G\in\mathcal{C} \implies f^{-1} (G) \in \mathcal{F}
をみたすとき, f は可測関数である。
可測関数の定義は G\in\mathcal{G} \implies f^{-1} (G) \in \mathcal{F} でした。これは \mathcal{G} の生成元の集合 \mathcal{C} だけについて G\in\mathcal{C} \implies f^{-1} (G) \in \mathcal{F} が言えれば,可測性が言えると主張しているわけですね。
略証をしておきましょう。上で取り上げた「逆像の性質」を用います。
略証
\mathcal{G}_0 = \{ G\subset Y\colon f^{-1}(G)\in\mathcal{F}\}
とすると,「逆像の性質」より \mathcal{G}_0 がσ-加法族であることは容易に確認できる。仮定より, \mathcal{C}\subset \mathcal{G}_0 なので, \mathcal{G}\subset \mathcal{G}_0 である。これより, f は可測性の定義をみたす。
証明終
実数上の可測関数
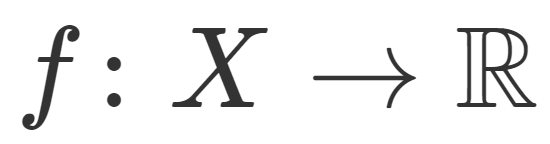
実数上の可測関数の定義と具体例
(X,\mathcal{F}) を可測空間, (\mathbb{R}, \mathcal{B}(\mathbb{R})) を実数 \mathbb{R} 上の標準的なボレル集合族としましょう。このとき, f\colon X\to \mathbb{R} が可測 (measurable) であるとは,
\large \color{red} U \in \mathcal{B}(\mathbb{R}) \implies f^{-1} (U) \in\mathcal{F}
となることを言います。一般的な可測関数の定義を焼き直ししただけですね。 \mathcal{B}(\mathbb{R}) = \sigma(\{ (-\infty, a] \colon a\in\mathbb{Q}\}) でしたから,上の定理1を用いることで,以下の定理が成立します。
定理2(σ-加法族の生成と可測関数)
(X,\mathcal{F}) を可測空間とする。 f\colon X\to\mathbb{R} が可測関数である必要十分条件は,任意の a\in \mathbb{Q} に対して
\large\color{red} \{ f\le a\} \in\mathcal{F}
が成立することである。
\{f\le a\} とは, \{x\in X\colon f(x)\le a\} を省略して書いています。 \{f\le a\} = f^{-1}((-\infty, a]) ですね。また, \mathcal{B}(\mathbb{R}) = \sigma(\{ (-\infty, a) \colon a\in\mathbb{Q}\}) でもありますから, \color{red}\{f< a\} \in\mathcal{F} としてもよいです。同じく \color{red} \{f\ge a\} \in\mathcal{F} や \color{red} \{f>a\}\in\mathcal{F} でも良いです。
具体例を挙げましょう。以下で, 1_A は定義関数です(→定義関数(指示関数,特性関数)とは)。
可測関数の具体例1
(X,\mathcal{F}) を可測空間とする。以下は可測関数 f\colon X\to\mathbb{R} の具体例である。
1.については,逆像 f^{-1} は \emptyset, A, A^c, X のいずれかであり,全て \mathcal{F} に入るため,可測関数ですね。
2.については, f^{-1} が A_1, \dots, A_n やその補集合の有限個の演算で書けることから,同じく全て \mathcal{F} に入るため,可測関数です。2.の形の関数を単関数 (simple function) といいます(→単関数とは何か~定義と可測関数の単関数近似~)。
3.は定理2.から明らかでしょう。
上3つから, f\colon \mathbb{R}\to \mathbb{R} における可測関数の例が挙げられます。
可測関数の具体例2
以下は可測関数 f\colon \mathbb{R}\to\mathbb{R} の具体例である。
なお,可測関数 f\colon X\to \mathbb{R} の代わりに,終域に \pm\infty を付加して,f\colon X\to [-\infty, \infty] を考えることも多いです。
可測関数の和・積・可算極限も可測関数
記事の最初の方で可測関数の合成が可測関数になることを軽く述べましたが,和・積・可算極限も可測関数になります。
定理(可測関数の和・積・可算極限も可測関数)
(X,\mathcal{F}) を可測空間, f,g \colon X\to \mathbb{R} を可測関数とする。このとき,
- f+ g も可測。
- \alpha\in\mathbb{R} に対し, \alpha f も可測。
- \alpha \in\mathbb{R} に対し,|f|^\alpha も可測 ( 0^0=1 と解釈)。
- fg も可測。
さらに \{f_n\} を可測関数の列とするとき,\sup_{n\ge 1} f_n(x) や \inf_{n\ge 1} f_n(x) も可測である。よって特に \limsup_{n\to\infty} f_n(x), \, \liminf_{n\to\infty}f_n(x) も可測である。
1,2.より, \alpha,\beta\in\mathbb{R} に対し, \alpha f+\beta g も可測です。
「さらに~」以下は「可算個」の上限や下限であることが本質で,非可算では成立しません。σ-加法族は可算個の和集合・共通部分についてしか閉じていなかったことを思い出してください。
証明
1. f+g が可測について
a\in\mathbb{Q} に対し,
\begin{aligned}&\{f+g< a\} \\&= \{ f<a-g\} \\ &=\bigcup_{r\in\mathbb{Q}}\bigl( \{ f< r\} \cap \{r< a-g\} \bigr)\\ &= \bigcup_{r\in\mathbb{Q}}\bigl( \{ f< r\} \cap \{g< a-r\} \in\mathcal{F}\end{aligned}
より, f+g は可測である。
2. \alpha f が可測について
\alpha =0 のとき明らか。 \alpha\ne 0 のとき, a\in\mathbb{R} に対し,
\{\alpha f\le a\} =\{f\le a/\alpha \}\in \mathcal{F}
より, \alpha f は可測である。
3. |f|^\alpha が可測について
\alpha =0 のとき明らか。 \alpha \ne 0 のとき, a>0 に対し,
\begin{aligned}&\{|f|^\alpha \le a\} \\&= \{ |f|\le a^{1/\alpha}\} \\ &= \{ -a^{1/\alpha} \le f\} \cap \{ f\le a^{1/\alpha}\} \in\mathcal{F} \end{aligned}
であるから, |f|^\alpha は可測である。
4. fg が可測について
fg= \dfrac{1}{4} \{|f+g|^2-|f-g|^2\} であることと,1-3.より, fg は可測である。
\sup_{n\ge 1} f_n(x), \inf_{n\ge 1} f_n(x) が可測について
\overline{f}(x) = \sup_{n\ge 1} f_n(x), \underline{f}(x)=\inf_{n\ge 1} f_n(x) と定める。 a\in\mathbb{R} に対し,
\begin{gathered}\{ \overline{f}\le a\} = \bigcap_{n=1}^\infty \{f_n\le a\} \in\mathcal{F}, \\ \{ \underline{f}\ge a\} = \bigcap_{n=1}^\infty \{f_n\ge a\} \in\mathcal{F} \end{gathered}
より, \overline{f},\underline{f} は可測である。
\limsup_{n\to\infty} f_n(x), \liminf_{n\to\infty}f_n(x) が可測について
\limsup_{n\to\infty} f_n(x) = \inf_{k\ge 1}\sup_{n\ge k} f_n(x), \liminf_{n\to\infty} f_n(x) = \sup_{k\ge 1} \inf_{n\ge k} f_n(x) より直ちに従う。
証明終
単関数による可測関数の近似
任意の可測関数 f\colon X\to \mathbb{R} は,単関数によって近似することが可能です。簡単のため,非負としましょう。
単関数 (simple function) とは,A_1,\dots, A_n\in\mathcal{F},\; a_1, \dots, a_n \in\mathbb{R} を用いて, \sum_{k=1}^n a_k 1_{A_k}(x) とかける関数のことです。「可測関数の具体例1」で取り上げたとおり,単関数は可測です。
定理(単関数による可測関数の近似)
f \colon X\to \mathbb{R} を非負可測関数としたとき,ある非負単関数列 \{f_n \} が存在して,各点で f_n \uparrow f とできる。
証明は以下の記事で行っています。