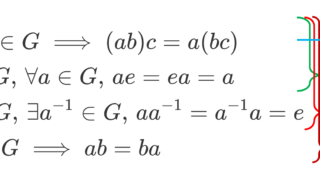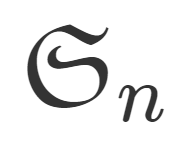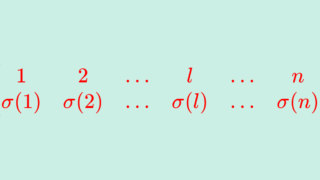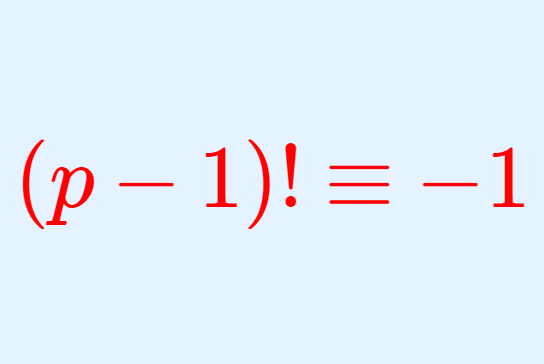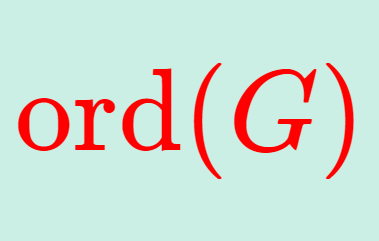群論における「部分群」とは,ある群の部分集合であって,それ自身も群になっているものを指します。これについて,定義とその判定方法について述べ,具体例を通して理解していきましょう。最後には部分群の性質も述べます。
部分群の定義と判定方法
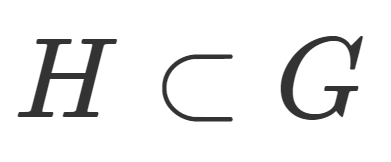
部分群の定義
定義(部分群)
G を群とする。空でない集合 H\subset G が部分群 (subgroup) であるとは, G と同じ演算によって, H も群となることである。
本記事では「部分群」といったときは空集合を考えないことにします。ポイントなのは, H は G と同じ演算でなければなりません。
話を進める前に,群の定義を復習しておきましょう。群とは,以下のような二項演算が定義されている集合のことです。
- a,b,c\in G\implies (ab)c = a(bc) (結合法則)
- \exists e \in G, \; a\in G \implies ae=ea=a (単位元の存在)
- \forall a\in G, \exists a^{-1}\in G, \; aa^{-1}=a^{-1}a=e (逆元の存在)
部分群は群ですから,上の性質をみたしていないといけません。
部分群の判定方法2つ
部分群かどうか判定する方法を2つ述べましょう。
定理1(部分群の判定方法1)
H\subset G が群 G の部分群である必要十分条件は
- e_G \in H (G の単位元は H に入る)
- a,b \in H \implies ab\in H (積に関して閉じている)
- a\in H \implies a^{-1} \in H (逆元に関して閉じている)
の全てが成立することである。
頭の中で部分群か確認するには,この方法が良いでしょう。証明は具体例の後に記述します。
基本的には上の定理を覚えておけば,部分群の判定には問題ないですが,実は上の3つは,1つの条件に集約することが可能です。それが以下の定理です。
定理2(部分群の判定方法2)
H\subset G が群 G の部分群である必要十分条件は
a,b\in H \implies ab^{-1}\in H
が成立することである。
ある群が部分群であることの証明を記すときは,この方法が簡便で良いでしょう。ただ,頭の中では,定理1を考えて「部分群である」と思う場面の方が多いと思います。
ただ,テキストを読んでいると,定理2をもってして部分群だとしている証明を見かけますから,しっかり理解しておくべきです。
定理2の証明も,具体例の後にしましょう。
部分群の具体例
いくつか部分群の具体例を挙げましょう。
例1(数の和).
\{0\} \subset \mathbb{Z}\subset \mathbb{Q}\subset \mathbb{R} \subset \mathbb{C} は全て和に関する \mathbb{C} の部分群である。
\mathbb{Z},\mathbb{Q},\mathbb{R} は和の演算による群 \mathbb{C} の部分集合であり,定理1の仮定をみたす(単位元 0 は存在し,演算は和・逆元に関して閉じている)ので, \mathbb{C} の部分群になります。 \{0\} は自明な部分群です。
例2(数の積).
集合 A に対して, A^* = A\setminus \{0\} とかくことにする。
\{1\} \subset \{\pm 1\} \subset \mathbb{Q}^*\subset \mathbb{R}^* \subset \mathbb{C}^* は全て積に関する \mathbb{C}^* の部分群である。
これも定理1をみたす(単位元 1 は存在し,演算は積・逆元に関して閉じている)ので,部分群であるとわかりますね。
例3(行列群).
n 次正則行列(可逆行列)全体の集合
\!\!\! \mathrm{GL}_n(\mathbb{R})\! = \! \{ A\!=\!(a_{ij})_{1\le i,j\le n} \!\mid \!a_{ij}\in\mathbb{R}, \det A \!\ne\! 0\}
は,積に関して群となる(一般線形群ということもある)。このとき,
は \mathrm{GL}_n(\mathbb{R}) の部分群である(特殊線形群ということもある)。
定理1に基づいて,部分群であることを確認してみましょう。まず単位行列について \det I=1 から I\in \mathrm{SL}_n(\mathbb{R}) ですね。これは \mathrm{GL}_n(\mathbb{R}) の単位元ですから,単位元はちゃんと \mathrm{SL}_n(\mathbb{R}) に入ります。
次に, A,B\in \mathrm{SL}_n(\mathbb{R}) とすると, \det (AB)=\det A \det B = 1 ですから, AB\in \mathrm{SL}_n(\mathbb{R}) であり, \det (A^{-1}) = (\det A)^{-1} = 1 ですから, A^{-1} \in \mathrm{SL}_n(\mathbb{R}) ですね。
よって,定理1がみたされたので,部分群であることが示せました。
例4(置換群).
置換 \sigma \colon \{1,2,\dots, n\}\to \{1,2,\dots, n\} 全体の集合 S_n は,写像の合成に関して群である(対称群という)。
このうち,偶置換全体の集合 A_n \subset S_n は S_n の部分群である(交代群という)。
ちょっと自分なりに考えてみてください。
対称群・交代群に関しては,以下で解説しています。
置換・偶置換については,以下で解説しています。
部分群の判定法(定理1,2)の証明
さて,上で述べた部分群の判定法の証明をしておきましょう。定理を再掲しておきます。
定理1再掲(部分群の判定方法1)
H\subset G が群 G の部分群である必要十分条件は
- e_G \in H (G の単位元は H に入る)
- a,b \in H \implies ab\in H (積に関して閉じている)
- a\in H \implies a^{-1} \in H (逆元に関して閉じている)
の全てが成立することである。
定理1の証明
十分性(上から下)は明らかなので,必要性(下から上)のみ示す。 H が群の定義をみたしているか確認する。
a,b,c\in H とすると G は群より (ab)c = a(bc) は成り立つ。また, e_G \in H であり,これは任意の h\in H に対して, e_Gh=he_G = h をみたすから, H の単位元も e_G と思える。また, a\in H なら a^{-1}\in H であるから, H には逆元も存在する。
以上から, H は群である。
証明終
定理2再掲(部分群の判定方法2)
H\subset G が群 G の部分群である必要十分条件は
a,b\in H \implies ab^{-1}\in H
が成立することである。
定理2の証明
十分性は明らかなので,必要性のみ示す。定理1の3条件に帰着できることを示せばよい。
条件より, a\in H なら aa^{-1} \in H から, e_G\in H である(定理1条件1)。 これより, e_G, a\in H から, e_G a^{-1} \in H すなわち a^{-1}\in H である(定理1条件3)。これより, a,b\in H とすると, a, b^{-1}\in H から, a(b^{-1})^{-1} \in H すなわち ab\in H も成り立つ(定理1条件2)。
証明終
無事証明できましたね。
部分群の性質5つ
最後に部分群の性質を記しておきましょう。
定理3(部分群の性質)
G を群とする。
- H\subset G を部分群とするとき,単位元について e_H = e_G である。すなわち, G,H の単位元は一致する。
- H\subset G を部分群とするとき,逆元について a^{-1_G} = a^{-1_H}\; (a\in H) である。すなわち, G,H における a\in H の逆元は一致する。
- G を可換群(アーベル群)とし, H \subset G を部分群とするとき, H も可換群(アーベル群)である。
- I \subset H\subset G とする。H が G の部分群であり,かつ I が H の部分群であれば, I は G の部分群でもある。
- \{H_\lambda\}_{\lambda \in\Lambda}\subset G を部分群の族とするとき, \bigcap_{\lambda \in\Lambda} H_\lambda も G の部分群である。
1,2.の証明は定理1の証明の途中で行っています。その他の証明は簡単のため省略します。