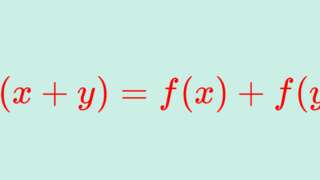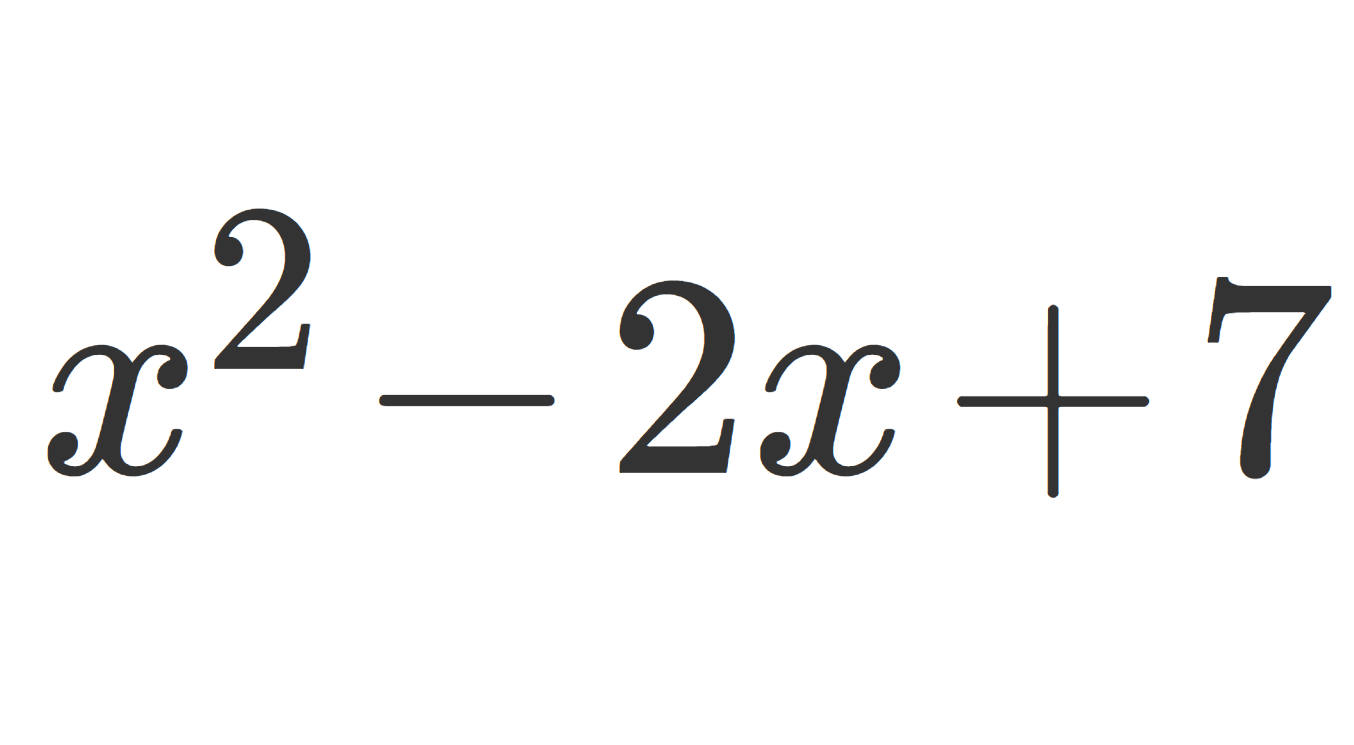凸関数と凸不等式(イェンセンの不等式)についてかなり詳しく

凸関数は，それ自身が研究対象の一つであり，凸解析 (convex analysis) といわれることがあります。凸関数・凹関数と凸不等式（イェンセンの不等式; イェンゼンの不等式; Jensen’s inequality）について，基本的なことを詳しくまとめましょう。

凸関数・凹関数とは～定義・イメージ・具体例～
1. 凸関数・凹関数の定義
2. 凸関数・凹関数のイメージと具体例
凸関数の重要な性質
より弱い意味での凸関数
関連する記事

凸関数・凹関数とは～定義・イメージ・具体例～

凸関数・凹関数の定義

定義1（凸関数・凹関数）

関数 $f\colon \R\to \R$ が任意の $x,y\in \R$ と $0\le \lambda\le 1$ に対し，

\color{red}f((1-\lambda) x+\lambda y)\le (1-\lambda) f(x)+\lambda f(y)

をみたすとき， $f$ を凸関数 (下に凸な関数; convex function) といい，

\color{red}f((1-\lambda) x+\lambda y)\ge (1-\lambda) f(x)+\lambda f(y)

をみたすとき， $f$ を凹関数 (上に凸な関数; concave function) という。

上の一つ目の凸関数に関する不等式を凸不等式 (convex inequality) またはイェンセンの不等式 (イェンゼンの不等式; Jensen’s inequality) といいます。

高校では，「上に凸な関数・下に凸な関数」という表現をすることが多いかもしれませんが，一般には「凸関数・凹関数」ということが多いです。上の凸関数の定義は，任意の $p+q=1,\, p,q\ge 0$ について，

\color{red}f(p x+q y)\le p f(x)+q f(y)

と言っても同じことですし，凹関数の定義は，任意の $p+q=1,\,p,q\ge 0$ について，

\color{red}f(p x+q y)\ge p f(x)+q f(y)

と言っても同じことです。さらに， $x\ne y$ かつ $-1<\lambda<1$ のとき常に

f((1-\lambda) x+\lambda y)< (1-\lambda) f(x)+\lambda f(y)

が成り立つなら，狭義凸関数 (strictly convex function) といい，

f((1-\lambda) x+\lambda y)>(1-\lambda) f(x)+\lambda f(y)

が成り立つなら，狭義凹関数 (strictly concave function) といいます。

また，関数 $f$ の定義域を $\R$ としましたが， $\R^n$ や， $\R^n$ の凸部分集合などでも構いません。今回は簡単のため， $f\colon \R\to\R$ のみを考えます。

凸関数・凹関数のイメージと具体例

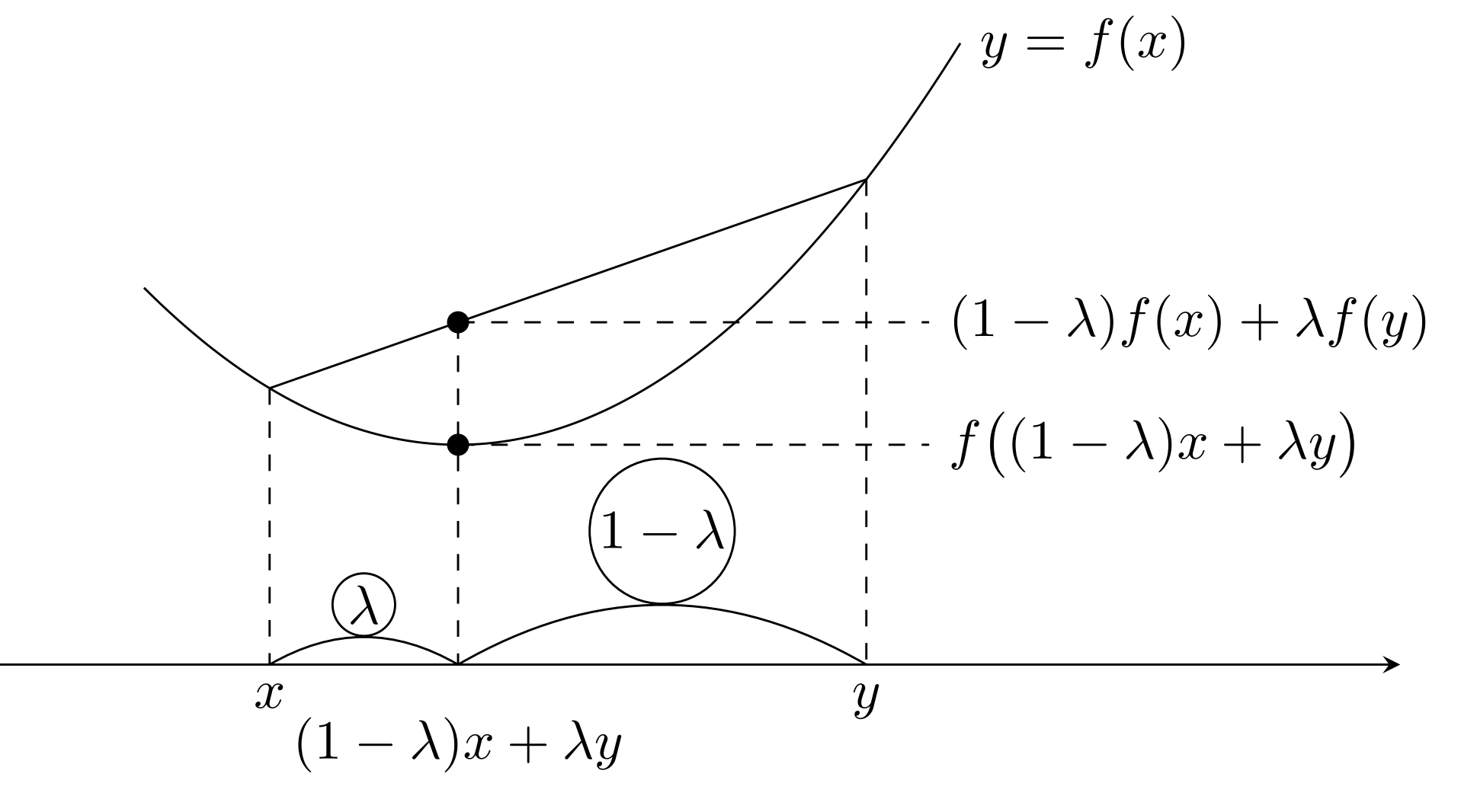
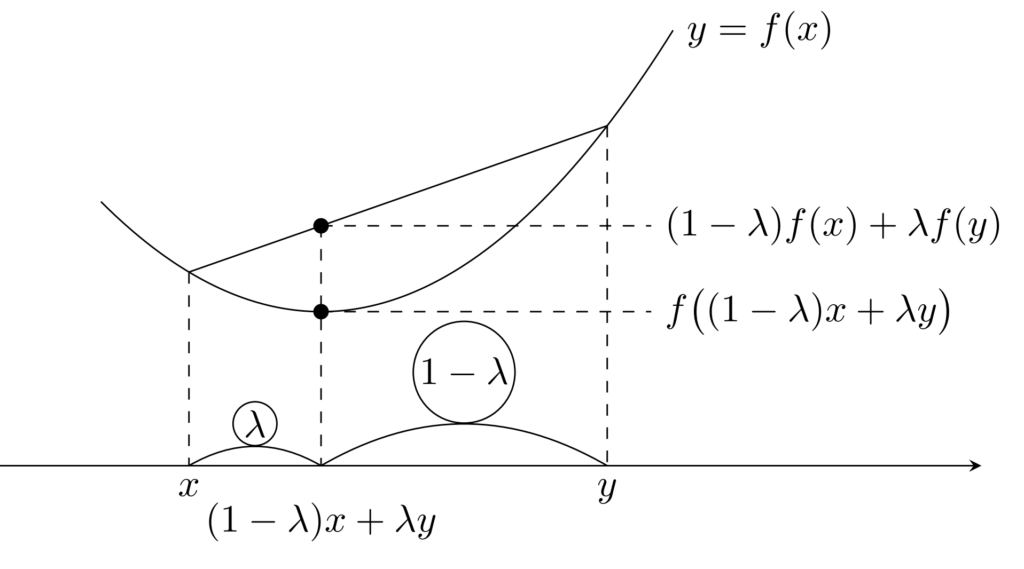
$x<y$ を固定して考えると，

\begin{aligned}f((1-\lambda) x+\lambda y)\le (1-\lambda) f(x)+\lambda f(y),& \\ 0\le \lambda \le 1& \end{aligned}

とは，以下の図のように，2点 $(x,f(x)), (y,f(y))$ を結んだ線分が $y=f(x)$ に重なるか，上側にあるといえます。 $x,y$ は任意ですから， $y=f(x)$ 上の2点を結ぶ線分が，常に $y=f(x)$ の上側にある(重なる場合を含む)ということになります。これが凸関数のイメージです。

凹関数は逆に2点 $(x,f(x)), (y,f(y))$ を結んだ線分が $y=f(x)$ より下側にある(重なる場合を含む)といえますね。以下の図のような感じです。

実際のところ，

$f$ は凹関数 $\iff -f$ は凸関数

です。これを踏まえれば，凸関数・凹関数の例を挙げることができます。

凸関数・凹関数の例

以下の関数 $f$ は凸関数であり， $-f$ は凹関数である。

$f(x)=x^2$
$f(x)=|x|$

1.が凸関数であることは， $f''(x)=2>0$ と後述する定理4から分かります。2.が凸関数であることは， $x,y\in \R,\, 0\le \lambda\le 1$ に対し，三角不等式より

\begin{aligned}|(1-\lambda) x+\lambda y|&\le |(1-\lambda) x|+|\lambda y| \\&= (1-\lambda) |x|+\lambda |y| \end{aligned}

であることから分かります。

凸関数の重要な性質

さて，先程述べたように，

$f$ は凹関数 $\iff -f$ は凸関数

ですから，凸関数を考えることと凹関数を考えることは表裏一体です。したがって，ここからは凸関数のみの性質について考えることにしましょう。

1. n個の凸不等式(イェンセンの不等式)

定理1（n個の凸不等式・イェンセンの不等式）

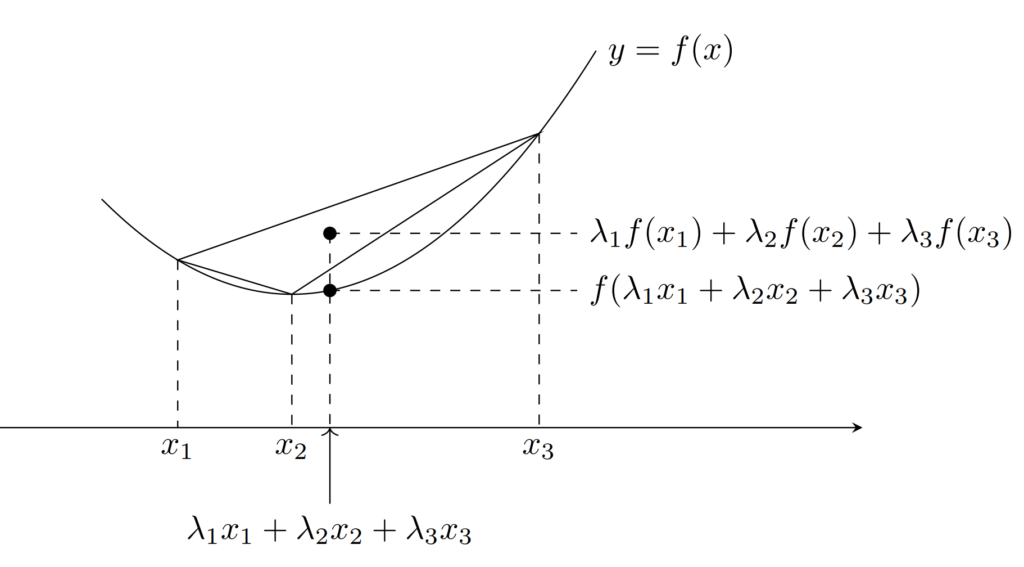
$f\colon \R\to\R$ を凸関数とする。このとき，任意の $n \ge 2$ と， $x_1,x_2,\dots, x_n \in \R$ と， $\sum_{k=1}^n \lambda_k=1$ をみたす $\lambda_1,\lambda_2,\dots, \lambda_n\ge 0$ に対し，

\color{red}\large f\left(\sum_{k=1}^n \lambda_k x_k \right)\le \sum_{k=1}^n \lambda_k f(x_k)

が成り立つ。

$n=2$ のときは，凸関数の定義の式と全く同じ意味です。本定理で特に $\lambda_1=\lambda_2=\dots =\lambda_n=1/n$ とすることで，

f\left(\frac{x_1+\dots+x_n}{n}\right)\le \frac{f(x_1)+\dots+f(x_n)}{n}

も成り立ちます。

定理1の証明

数学的帰納法で示す。 $n=2$ のときは凸関数の定義より直ちに従う。

ある $n$ で定理が成り立っているとする。このとき， $\color{red}f\left(\sum_{k=1}^{n+1} \lambda_k x_k \right)\le \sum_{k=1}^{n+1} \lambda_k f(x_k)$ を示そう。まず，

\begin{aligned}&f\left(\sum_{k=1}^{n+1} \lambda_k x_k \right)\\&= f\left(\textcolor{blue}{\left(\sum_{k=1}^{n}\lambda_k\right)} \frac{\sum_{k=1}^n \lambda_k x_k}{\sum_{k=1}^{n}\lambda_k } + \textcolor{blue}{\lambda_{n+1}}x_{n+1}\right) \end{aligned}

である。ただし， $\sum_{k=1}^{n}\lambda_k\ne 0$ とした( $=0$ のとき，赤字の式が成り立つのは自明である)。ここで， $\textcolor{blue}{\left(\sum_{k=1}^{n}\lambda_k\right)} +\textcolor{blue}{\lambda_{n+1}}=1$ より，凸関数の定義から，

\!\!\!\! \begin{aligned}& f\left(\textcolor{blue}{\left(\sum_{k=1}^{n}\lambda_k\right)} \frac{\sum_{k=1}^n \lambda_k x_k}{\sum_{k=1}^{n}\lambda_k } + \textcolor{blue}{\lambda_{n+1}}x_{n+1}\right)\\ &\le \textcolor{blue}{\left(\sum_{k=1}^{n}\lambda_k\right)} f\left( \frac{\sum_{k=1}^n \lambda_k x_k}{\sum_{k=1}^{n}\lambda_k }\right) + \textcolor{blue}{\lambda_{n+1}}f(x_{n+1}) \\ &={\small{\left(\sum_{k=1}^{n}\lambda_k\right)} \textcolor{green}{f\left( \sum_{k=1}^n \frac{\lambda_k}{\left(\sum_{k=1}^{n}\lambda_k\right)} x_k \right)}+ {\lambda_{n+1}}f(x_{n+1})} \end{aligned}

さらに緑の部分について， $\sum_{k=1}^n \frac{\lambda_k}{\left(\sum_{k=1}^{n}\lambda_k\right)}=1$ より，帰納法の仮定から

\small \!\!\!\!\! \begin{aligned}&\left(\sum_{k=1}^{n}\lambda_k\right)\textcolor{green}{f\left( \sum_{k=1}^n \frac{\lambda_k}{\left(\sum_{k=1}^{n}\lambda_k\right)} x_k \right)}+ \lambda_{n+1}f(x_{n+1})\\ &\le\left(\sum_{k=1}^{n}\lambda_k\right) \textcolor{green}{\sum_{k=1}^n \frac{\lambda_k}{\left(\sum_{k=1}^{n}\lambda_k\right)}f( x_k )}+ \lambda_{n+1}f(x_{n+1}) \\ &=\sum_{k=1}^n \lambda_k f(x_k)+ \lambda_{n+1}f(x_{n+1}) \\ &=\sum_{k=1}^{n+1} \lambda_k f(x_k) \end{aligned}

以上をまとめると，赤字の式が示せた。

証明終

2. 凸関数の弦の傾き

定理2（凸関数の弦の傾き）

$f\colon \R\to\R$ が凸関数である必要十分条件は，任意の $x_1<x_2<x_3$ に対し，

\small \color{red} \frac{f(x_2)-f(x_1)}{x_2-x_1}\le \frac{f(x_3)-f(x_1)}{x_3-x_1}\le \frac{f(x_3)-f(x_2)}{x_3-x_2}

が成り立つことである。

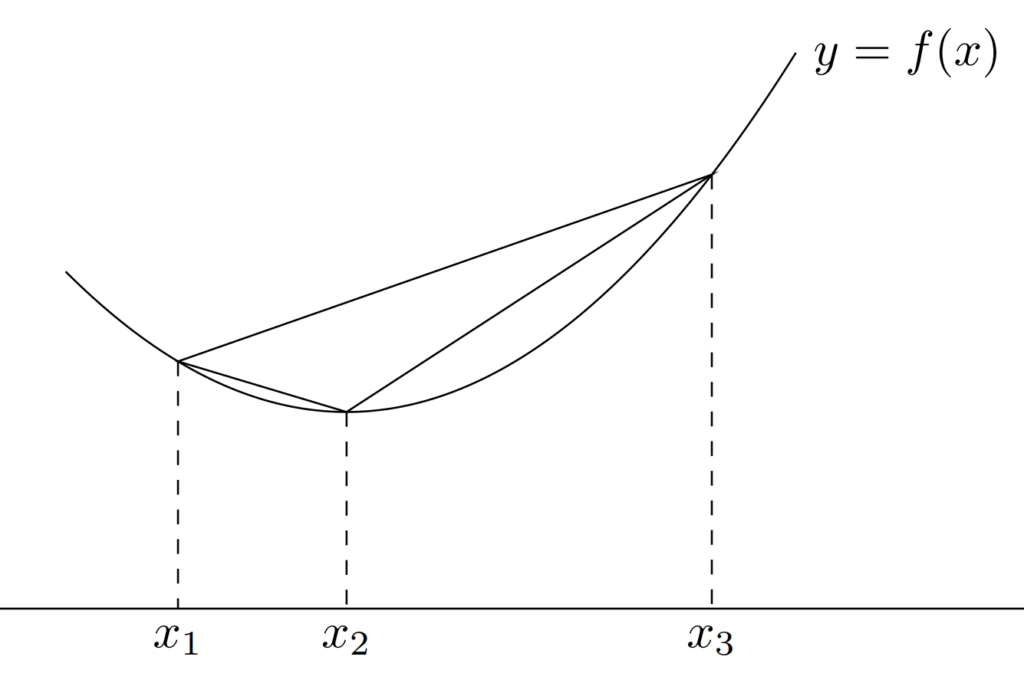
上図の各直線の傾きを考えてもわかるように，赤字の式は， $f$ の「平均変化率」は単調に増加するということを意味しています。

より一般に，

\begin{align} &{\scriptsize (x_3-x_1)f(x_2)\le (x_2-x_1)f(x_3)+ (x_3-x_2)f(x_1) } \\ &\iff \frac{f(x_2)-f(x_1)}{x_2-x_1}\le \frac{f(x_3)-f(x_1)}{x_3-x_1} \\ &\iff \frac{f(x_3)-f(x_1)}{x_3-x_1} \le \frac{f(x_3)-f(x_2)}{x_3-x_2}\end{align}

が成り立つため，定理内の赤字の2本の不等式は，片方のみで構いません。実際， $(1)\implies(2)$ は $(1)$ の両辺 $(x_3-x_1)f(x_1)$ を引いてから両辺 $(x_2-x_1)(x_3-x_2)>0$ で割ると $(2)$ になり，逆の計算をすることで $(2)\implies (1)$ も言えます。

同様に $(x_3-x_1)f(x_3)$ を引いてから $- (x_3-x_2)(x_3-x_1)<0$ で割ることで， $(1)\implies (3)$ が，逆の計算をすれば $(3)\implies (1)$ が証明できます。

定理2の証明

凸関数の定義式

f((1-\lambda) x+\lambda y)\le (1-\lambda) f(x)+\lambda f(y)

に対して， $x=x_1, y=x_3, \lambda=\frac{x_2-x_1}{x_3-x_1}$ とすると，定理の主張直後の $(1)$ 式になり，逆に $(1)$ 式で $x_1=x, x_3=y, x_2=(1-\lambda) x +\lambda y$ とすると凸関数の定義式に戻る。

証明終

本定理より，次の系も従います。

系（凸関数の性質）

$f\colon \R\to\R$ が凸関数であるとき，以下の3つのうちいずれかが成り立つ。

$f$ は広義単調増加である
$f$ は広義単調減少である
ある $a\in\R$ が存在して， $f$ は区間 $(-\infty, a]$ で広義単調減少，区間 $[a,\infty)$ で広義単調増加である。

3. 凸関数の連続性・微分可能性

凸関数と言えば，必ず連続であるし，またほとんどの点で微分可能であることが証明できます。

定理3（凸関数の連続性・微分可能性）

凸関数は連続関数である。また，高々可算個の点を除いて微分可能である。

凸関数は全ての点で微分可能とは限りません。最初の具体例で挙げた通り， $f(x)=|x|$ は凸関数ですが， $x=0$ で微分不可能ですね。

定理3の証明

上の定理2で，任意の $x_1<x_2<x_3$ に対して，

\small \frac{f(x_2)-f(x_1)}{x_2-x_1}\le \frac{f(x_3)-f(x_1)}{x_3-x_1}\le \frac{f(x_3)-f(x_2)}{x_3-x_2}

を示した。下に有界な単調減少極限は収束することから，右微分

f'_+(x_1)=\lim_{y\to x_1+} \frac{f(y)-f(x_1)}{y-x_1}

は収束し，同様に上に有界な単調増加極限は収束することから，左微分

f'_-(x_3)=\lim_{y\to x_3-} \frac{f(x_3)-f(y)}{x_3-y}

も収束する。また， $x<y$ に対し，

f'_-(x)\le f'_+(x)\le f'_-(y)\le f'_+(y)\tag{*}

が成り立つことも示せる。

連続性について

以下複号同順で，

\begin{aligned} f(x+h)-f(x)&=\frac{f(x+h)-f(x)}{h}\cdot h \\ &\xrightarrow{h\to 0\pm} f'_{\pm}(x)\cdot 0=0\end{aligned}

であるから， $\lim_{h\to 0} \{f(x+h)-f(x)\} =0$ である。

可算個の点を除いて微分可能について

$\text{ (*)}$ 式より， $f'_+$ は広義単調増加関数であるから，Frodaの定理より，不連続点は高々可算個しかない。同じ $\text{ (*)}$ 式より， $f'_+$ の連続点においては $f'_+=f'_-$ が成立するから，微分可能である。

証明終

連続性については，定理2を用いない直接的な別証を紹介しておきましょう。

凸関数の連続性の別証

$x\in\R$ とし， $\delta\ne 0$ を適当に取る( $\delta=1$ とかでもよい)。 $0\le \lambda \le 1$ に対し，

\begin{aligned} f(x+\lambda \delta)&=f((1-\lambda)x+\lambda(x+\delta)) \\ &\le (1-\lambda) f(x)+\lambda f(x+\delta) \end{aligned}

より変形して，

\color{blue}f(x+\lambda \delta)-f(x) \le \lambda \{ f(x+\delta)-f(x) \}.

また，

\begin{aligned}f(x)&=f\left( \frac{x+\lambda \delta}{1+\lambda} + \frac{\lambda(x-\delta)}{1+\lambda}\right) \\ &\le \frac{1}{1+\lambda }f(x+\lambda \delta)+\frac{\lambda}{1+\lambda} f(x-\delta) \end{aligned}

を変形して，

\color{blue} f(x+\lambda\delta)-f(x)\ge -\lambda\{ f(x-\delta)-f(x)\}.

青字の二式より，

\small \begin{aligned} &| f(x+\lambda\delta)-f(x)| \\&\le \lambda \max\{ |f(x+\delta)-f(x)|, |f(x-\delta)-f(x)| \} \\ &\xrightarrow{\lambda\to 0} 0\end{aligned}

となるため， $f$ は $x$ で連続である。

証明終

4-5. 凸関数と1階微分・2階微分

以下の定理は，高校生のときに習った人も多いかもしれません。

定理4（凸関数と1階微分・2階微分）

$f \colon \R\to\R$ が微分可能とする。このとき， $f$ は凸関数 $\iff f'$ は広義単調増加である。

特に， $f$ が2階微分可能ならば， $f$ は凸関数 $\iff f''(x)\ge 0$ である。

もし $f$ が2階微分可能ならば， $f'$ が単調増加 $\iff f''\ge 0$ ですから，前半が言えれば後半は明らかです。

ここまで様々な定理を証明してきましたが，それらを用いると本質を貫いていて非常に見通しがよいです。ただ，一方で本定理だけを最速で理解したいという需要もあるでしょうから，これまでの定理を用いた方法と，そうでない方法の両方を紹介しておきましょう。

定理4の証明

定理3を使う見通しの良い手法

$\implies$ について $f$ は微分可能であるから，定理3の証明中において，常に $f'_+=f'_-$ である。 $f'_+, f'_-$ は広義単調増加であるから，示せた。

$\impliedby$ について $f'$ が広義単調増加ならば， $x_1<x_2<x_3$ に対して，

\begin{aligned} \frac{\int_{x_1}^{x_2} f'(x)\, dx }{x_2-x_1} \le \frac{\int_{x_1}^{x_3} f'(x)\, dx }{x_3-x_1}\le \frac{\int_{x_3}^{x_2} f'(x)\, dx }{x_3-x_2} \end{aligned}

が成り立つため，

\small \frac{f(x_2)-f(x_1)}{x_2-x_1}\le \frac{f(x_3)-f(x_1)}{x_3-x_1}\le \frac{f(x_3)-f(x_2)}{x_3-x_2}

となって定理3に帰着する。

定理3を使わない手軽な手法

$\implies$ について 2階微分可能な場合に限って示す。このとき，一般に

f''(x)=\lim_{h\to 0} \frac{f(x+h)+f(x-h)-2f(x)}{h^2}

である。右辺の $\lim$ の中身は常に非負なので， $f''\ge 0$ となる。

$\impliedby$ について $x<y$ とし， $0\le \lambda \le 1$ に対して，

\small g(\lambda)=(1-\lambda) f(x)+\lambda f(y)-f((1-\lambda) x+\lambda y)

とおく。このとき，

\small g'(\lambda)=f(y)-f(x) -(y-x)f'((1-\lambda) x+\lambda y)

である。 $f'$ は広義単調増加なので， $g'$ は広義単調減少である。 $g(0)=g(1)=0$ より，ロルの定理(平均値の定理)から， $g'(c)=0$ となる $0<c<1$ が存在するため， $g'$ は

g'(\lambda) \begin{cases} \ge 0 & 0\le \lambda\le c,\\ \le 0 & c\le \lambda \le 1 \end{cases}

となる。これを基に $g$ の増減を考えることで， $g\ge 0$ が分かるため， $(1-\lambda) f(x)+\lambda f(y) \ge f((1-\lambda) x+\lambda y)$ が示せて証明が終わる。

証明終

特に，今までの定理3を用いない手法における $f$ は凸関数 $\impliedby f'$ は広義単調増加の証明については，高校生でも手軽に証明でき，知っておくと受験で役立つかもしれません。

なお， $\implies$ については， $f''$ の連続性があれば簡単に証明できます。実際， $f''<0$ となる点があるとすれば，連続性からその点の周りで $f''<0$ となり，その区間で狭義凹関数になって矛盾するからです。

定理3で，凸関数 $f$ は高々可算個の点を除いて微分可能と紹介しました。すなわち， $f$ が微分可能な点全体の集合を $A\subset \R$ とすると， $\R\setminus A$ は高々可算集合です。 $x\in A$ に対し2階微分

f''(x)=\lim_{y\to x, \, y\in A}\frac{f'(y)-f'(x)}{y-x}\tag{*}

を考えます。このとき，以下の定理が知られています。

定理5（アレクサンドロフの定理）

$f$ が凸関数ならば，ほとんどいたるところ2階微分可能で，2階微分できる点で常に $f''\ge 0$ が成り立つ。

ただし，2階微分可能とは直前の式 $\text{(*)}$ の意味とする。

「ほとんどいたるところ」というのは，測度論の言葉で，ルベーグ測度 $0$ のある集合を除いてという意味です(→ほとんどいたるところ(almost everywhere, a.e.)の議論)。

証明

$f$ を凸関数とすると，定理3より高々可算個の点を除いて微分可能で， $f'$ はその上で広義単調増加である。単調関数はほとんどいたるところ微分可能であるから， $f'$ はほとんどいたるところ微分可能となる。微分可能な点では，

f''(x)=\lim_{y\to x, \, y\in A}\frac{f'(y)-f'(x)}{y-x}

が成り立つが， $f'$ は広義単調増加だから，上式の $\lim$ 内は常に $0$ 以上である。従って， $f''(x)\ge 0$ となる。

証明終

6. 凸関数と接線の位置関係

定理6（凸関数と接線の位置関係）

微分可能な凸関数のグラフの接線は，凸関数上かその下側にくる。

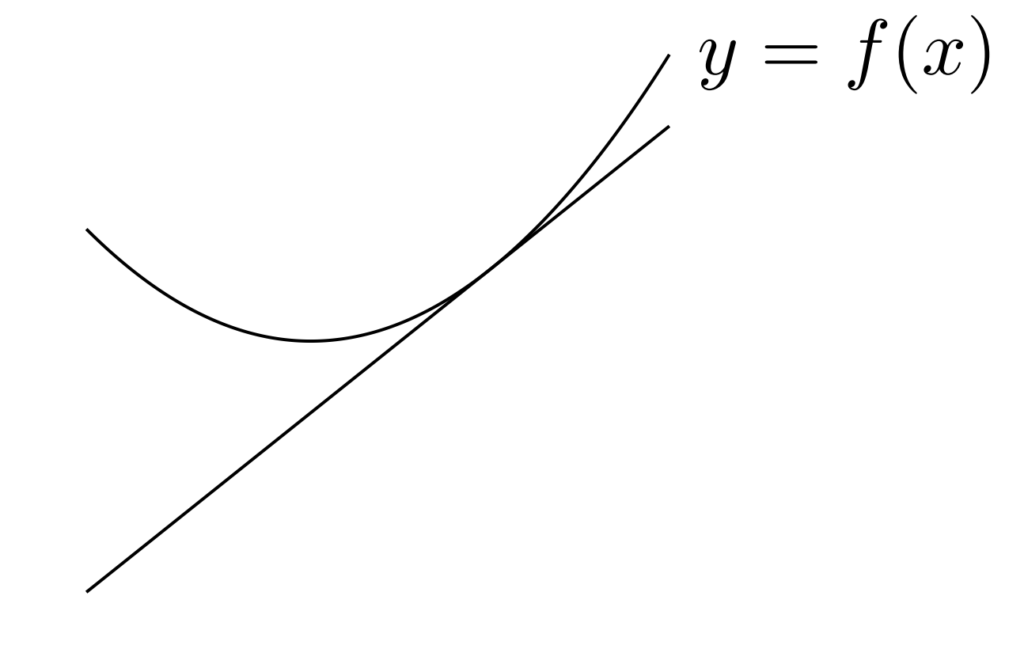
証明は簡単です。

定理6の証明

微分可能な凸関数 $f$ の $a$ における接線 $y=g(x)$ は $g(x)=f'(a)(x-a)+f(a)$ である。ここで，

\begin{aligned} f(x)-g(x)&=f(x)-\{f'(a)(x-a)+f(a)\} \\&= f(x)-f(a) -f'(a)(x-a)\end{aligned}

$a<x$ とすると，平均値の定理より， $f(x)-f(a)=f'(c)(x-a)$ となる $a<c<x$ が存在する。ゆえに，

f(x)-g(x)=\{f'(c)-f'(a)\}(x-a)

となる。定理4より， $f'(c)\ge f'(a)$ なので， $f(x)\ge g(x)$ が示せた。

$x<a$ のときも同じ議論である。

証明終

7. 凸関数の和・合成・逆関数など

凸関数と和や合成・逆関数について述べておきましょう。

定理7（凸関数の和・合成・逆関数など）

$f,g$ が凸関数で， $a,b>0$ を定数としたとき， $af+bg$ も凸関数である。
$\{f_n\}$ が凸関数の列で， $f_n \xrightarrow{n\to\infty} f$ (各点収束)であるなら， $f$ も凸関数である。
$f_1,f_2$ を凸関数としたとき， $f=\max\{f_1,f_2\}$ も凸関数である。
$f$ が凸関数でかつ単調増加のとき， $f^{-1}$ は凹関数である。
$f$ が凸関数でかつ単調減少のとき， $f^{-1}$ は凸関数である。
$f$ が凸関数で， $g$ が凸関数かつ単調増加であるとき， $g\circ f$ は凸関数である。
$f$ が凸関数で， $g$ が凹関数かつ単調減少であるとき， $g\circ f$ は凹関数である。

証明は，愚直にやるだけなので省略します。

8. 凸関数と凸集合

凸関数と凸集合には密接な関係があります。

定理8（凸関数と凸集合）

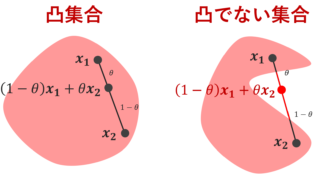
$f\colon \R\to \R$ が凸関数である必要十分条件は， $y=f(x)$ の上側の集合

A=\{ (x, y)\in \R^2 \mid y\ge f(x)\}

が凸集合になることである。

凸集合は凸集合とは何かをわかりやすく～定義と性質～で解説しています。証明は，定義に従ってやるだけなので省略します。

より弱い意味での凸関数

凸関数の定義は，もう少し弱い意味で定義することがあります。これも紹介しておきましょう。

中点凸関数の定義

定義2（中点凸関数）

関数 $f\colon \R\to\R$ が任意の $x,y\in\R$ に対し，

\large \color{red}f\left(\frac{x+y}{2}\right)\le \frac{f(x)+f(y)}{2}

が成り立つとき， $f$ は中点凸関数 (midpoint convex function) という。

逆に，

f\left(\frac{x+y}{2}\right)\ge \frac{f(x)+f(y)}{2}

なら中点凹関数 (midpoint concave function) といいます。

なお，本サイトでは全て $f\colon \R\to\R$ で述べますが，凸集合 $D\subset \R^n$ として $f\colon D\to \R$ としてもほぼ同じです。

凸関数 ⇔ 連続な中点凸関数

定理9（凸関数 $\iff$ 連続な中点凸関数）

関数 $f\colon \R\to \R$ が凸関数である必要十分条件は連続かつ中点凸関数であることである。

定理9の証明

凸関数 $\implies$ 連続な中点凸関数は定理3よりいえる。

凸関数 $\impliedby$ 連続な中点凸関数について

$0\le \lambda\le 1$ に対し， $\{\lambda_n\}\subset\mathbb{Q}\cap [0,1]$ で $\lambda_n \to \lambda$ となるものを取る。

後述する定理10より，

\!\!\!f((1-\lambda_n) x+\lambda_n y)\le (1-\lambda_n) f(x)+\lambda_n f(y)

である。 $f$ は連続より，両辺 $n\to\infty$ とすることで，

f((1-\lambda) x+\lambda y)\le (1-\lambda) f(x)+\lambda f(y)

となる。

証明終

さて今度は，上の定理で利用した以下の定理を証明しましょう。

定理10（中点凸関数の性質）

$f\colon \R\to\R$ を中点凸関数とする。このとき，任意の $\color{red}\lambda\in \mathbb{Q}\cap [0,1]$ に対して，

\color{red} f((1-\lambda) x+\lambda y)\le (1-\lambda) f(x)+\lambda f(y)

が成り立つ。

上の式で $\lambda\in [0,1]$ とした式が凸関数の定義ですね。より弱い中点凸関数の場合は， $\lambda$ を有理数に制限した凸不等式が成立するわけです。

定理10の証明

まず $x_1,\dots, x_n\in \R$ に対し，

\color{red} f\left(\frac{x_1+\dots+x_n}{n}\right)\le \frac{f(x_1)+\dots +f(x_n)}{n}

を示す。中点凸関数の定義と帰納法により，任意の整数 $p\ge 1$ と $x_1,\dots, x_{2^p}\in \R$ に対し，

\begin{align} f\left(\frac{1}{2^p} \sum_{k=1}^{2^p} x_k\right) \le \frac{1}{2^p}\sum_{k=1}^{2^p} f(x_k). \tag{\#}\end{align}

任意の $n \ge 1$ と $x_1,\dots, x_n\in\R$ を取る。これに対し， $n<2^p$ となる整数 $p\ge 1$ を取り，さらに $x_{n+1},x_{n+2},\dots ,x_{2^p}$ を

\begin{aligned}x_{n+1}=x_{n+2}=\dots =x_{2^p} = \frac{1}{n}\sum_{k=1}^n x_k \end{aligned}

と定める。このとき，

\begin{aligned}\frac{1}{2^p}\sum_{k=1}^{2^p} x_k &= \frac{1}{2^p}\left(\sum_{k=1}^{n} x_k + \sum_{k=n+1}^{2^p} x_k \right) \\ &= \frac{1}{2^p}\left(\sum_{k=1}^{n} x_k + \frac{2^p-n}{n}\sum_{k=1}^{n} x_k \right)\\ &= \frac{1}{n}\sum_{k=1}^{n} x_k. \end{aligned}

$(\#)$ 式にこれらを適用して，

\begin{aligned}&f\left(\frac{1}{n}\sum_{k=1}^{n} x_k \right) = f\left(\frac{1}{2^p} \sum_{k=1}^{2^p} x_k\right)\\ &\le \frac{1}{2^p}\sum_{k=1}^{2^p} f(x_k) \\ &= \frac{1}{2^p}\left\{\sum_{k=1}^{n} f(x_k)+(2^p-n) f\left(\frac{1}{n}\sum_{k=1}^{n} x_k \right)\right\}. \end{aligned}

両端辺を整理して，

n f\left(\frac{1}{n}\sum_{k=1}^{n} x_k \right)\le \sum_{k=1}^{n} f(x_k)

となり，両辺 $n$ で割れば証明冒頭の赤字の不等式(以下の赤字の不等式)が示せた。最後に定理を示そう。 $\lambda=\mathbb{Q}\cap (0,1)$ を $\lambda =m/n$ ( $m,n\ge 1$ を互いに素な整数)と表すことにする。

\color{red} f\left(\frac{x_1+\dots+x_n}{n}\right)\le \frac{f(x_1)+\dots +f(x_n)}{n}

において， $x_1=\dots =x_{n-m}=x,\; x_{n-m+1}=\dots = x_n=y$ と定めると，

\small f\left(\frac{(n-m) x+my}{n}\right)\le \frac{(n-m) f(x)+mf(y)}{n}

となる。すなわち， $f((1-\lambda) x+\lambda y)\le (1-\lambda) f(x)+\lambda f(y)$ である。

証明終

中点凸関数が連続である条件

上で，「凸関数 ⇔ 中点凸関数かつ連続」を示しました。では，中点凸関数はどういったときに連続になるかを考えましょう。実は，中点凸関数が連続であるためには，単にある1点の近傍で上に有界であればよいです。あるいは，可測でも構いません。

定理11（中点凸関数が連続である条件）

中点凸関数 $f$ について，以下のいずれかが成り立つなら，連続である。

ある1点の近傍で上に有界である
$f$ は可測である。

本定理により，たとえば「凸関数 ⇔ 中点凸関数かつ可測」も言えるわけですね。

また，本定理により，中点凸関数 $f$ は「全ての点で連続」か「全ての点で不連続」かのどちらかが成り立つことが分かります。1点で連続ならば，その点の周りで有界ですから，上の定理が使えて連続関数になってしまいます。

証明は少々長いですが，平易にかいたつもりなので，頑張りましょう。2.の証明は専門的な定理を用います。

定理11の証明

1. $f$ がある1点の近傍で上に有界なら連続であること

1-1. まず， $f$ は任意の点の近傍で上に有界(局所的上に有界)であることを示す

$(x_0-r, x_0+r)$ で上に有界であると仮定する。すなわち，

u\in (x_0-r, x_0+r)\implies f(u)\le M

とする。このとき，任意の $x\ne x_0$ に対し， $\left(x-r/2, x+r/2\right)$ で上に有界であることを示そう。まず， $x=(x_0+y_0)/2$ となる $y_0\in \R$ を定める。

$v\in \left(x-r/2, x+r/2\right)$ を任意に一つ取る。これに応じて， $v=(u+y_0)/2$ となる $u$ を定めると，

|u-x_0|=|2v-y_0-x_0|=2|v-x|< r

であるから， $u\in (x_0-r, x_0+r)$ である。したがって，

\begin{aligned} f(v)=f\left( \frac{u+y_0}{2} \right)&\le \frac{f(u)+f(y_0)}{2}\\&\le \frac{M+f(y_0)}{2}\end{aligned}

となって，右辺は $v\in \left(x-r/2, x+r/2\right)$ の取り方に依らないから，1-1.が示せた。

1-2. 次に， $f$ は任意の点の近傍で有界(局所有界；上にも下にも局所有界)を示す

1-1.を示したので，あと示すべきは $(x_0-r,x_0+r)$ で上に有界 $(f(u)\le M)$ なら，同じ区間で下にも有界なことある。 $u\in (x_0-r, x_0+r)$ を任意に取る。これに応じて， $x_0=(u+y)/2$ となる $y\in\R$ をとる。 $|y-x_0|=|u-x_0|<r$ より， $y\in (x_0-r, x_0+r)$ である。ここで，中点凸関数の定義から

f(x_0)\le \frac{f(u)+f(y)}{2}

なので，

f(u) \ge 2f(x_0)-f(y)\ge 2f(x_0)-M.

右辺は $u\in (x_0-r, x_0+r)$ の取り方に依らないから，下に有界が示せた。

1-3. 最後に， $f$ は連続であることを示す。

$x\in \R$ とする。1-2.より， $f$ は $x$ のまわりで有界なため，

\begin{aligned} M(x)&=\max\{ \limsup_{y\to x} f(y) , f(x)\},\\ m(x)&= \min\{\liminf_{y\to x} f(y), f(x)\} \end{aligned}

が共に有限値となる。当然，

m(x)\le f(x)\le M(x) \tag{i}

である。limsup, liminf の定義より，ある $\{ u_n\},\{v_n\}\subset \R$ が存在して，

\begin{aligned}\lim_{n\to\infty} u_n =x, \quad &\lim_{n\to\infty} f(u_n) =M(x), \\ \lim_{n\to\infty} v_n =x, \quad&\lim_{n\to\infty} f(v_n) =m(x)\end{aligned}

とできる。さらに， $\{x_n\}$ を $u_n =(v_n+x_n)/2$ すなわち $x_n=2 u_n-v_n$ と定める。すると， $\lim_{n\to\infty} x_n=x$ であり，

f(u_n)\le \frac{f(v_n)+f(x_n)}{2}

が成り立つ。これを変形すると， $f(x_n)\ge 2f(u_n)-f(v_n)$ であり，両辺 $\liminf_{n\to\infty}$ とすると，

$\liminf_{n\to\infty} f(x_n) \ge 2M(x)-m(x)$

を得る。一方で， $\lim_{n\to\infty} x_n=x$ と $M(x)$ の定義より， $M(x)\ge \liminf_{n\to\infty} f(x_n)$ でなければならない。故に， $M(x)\ge 2M(x)-m(x)$ であり，整理すると $M(x)\le m(x)$ となる。これと $\text{(i)}$ 式より，

m(x)= f(x)=M(x)

でなければならないが，これは $f$ が $x$ で連続であることを意味する。

2. 可測なら連続であること

$f\colon \R\to\R$ を可測とし， $\mu$ をルベーグ測度とする。 $n\in\mathbb{Z}$ に対し，

A_n = \{x\in\R\mid f(x)\le n\}

とおくと， $\{A_n\}$ は可測な単調増大列で， $\bigcup_{n\in\mathbb{Z}} A_n=\R$ であるから， $\mu(A_{n_0})>0$ となる $n_0\in\mathbb{Z}$ が存在する。

$A_{n_0}$ 上 $f\le n_0$ であるから， $A_{n_0}$ 上 $f$ は上に有界である。ここで， $a,b\in A_{n_0}$ とすると，

\begin{aligned}f\left(\frac{a+b}{2}\right) \le \frac{f(a)+f(b)}{2}\le n_0\end{aligned}

であるから， $f$ は $\frac{A_{ n_0}+A_{n_0}}{2} = \left\{\frac{a+b}{2}\mid a,b\in A_{n_0}\right\}$ においても上に有界である。シュタインハウスの定理より， $\frac{A_{ n_0}+A_{n_0}}{2}$ は区間を含むから，1.に帰着できる。

証明終