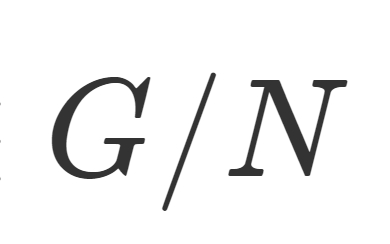代数学における「準同型写像・同型写像」とは,代数の演算の構造を保つ写像のことを指します。とくに,同じ代数構造を持つ2つの集合に同型写像が定まれば,その2つは「同じもの」として扱うことが可能です。
準同型写像・同型写像の定義・性質について,群・環・体それぞれについて分けて解説していきましょう。
群の準同型写像・同型写像
まずは,群の間の準同型写像・同型写像を定義していきましょう。
群準同型写像・群同型写像の定義
定義1(群の準同型・同型)
\color{red}\large f(ab) = f(a)f(b)\quad (a,b\in G)
をみたすとき, f を群の準同型 (homomorphism) という。
さらに f が全単射なら群の同型 (isomorphism) といい,\color{red} G\simeq H や \color{red}G\cong H とかく。

群の準同型とは「積を取ってから写したものと,写してから積を取ったものが等しいものだ」と言っているんですね。ある意味,群の準同型とは,群の構造を保つ写像といえるわけです。
同型とは,群として同じ構造であるという意味です。同型ならば,群として全く同じものであると思って差し支えありません。
f が全単射なら,逆写像 f^{-1} も同型になっていることが分かります(→定理1.5)。だからこそ「全単射」だけで「同型」と言ってしまっていい訳です。
なお,同型写像は \color{red} f\colon G\stackrel{\simeq}{\longrightarrow}H のような書き方をすることもあります。また,\color{red} G\simeq H ( G と H が同型 (isomorphic)) とは, G,H 間に同型写像が存在することを指します。
群準同型写像の性質
群準同型写像の性質を確認しましょう。
定理1(群準同型の性質)
G,H を群とし, f\colon G\to H を群の準同型とする。このとき,
- f(e_G) = e_H.
- g\in G に対し, f(g^{-1}) = f(g)^{-1}.
- \operatorname{Ker} f =\{ g\in G\mid f(g)=e_H\}, \; \operatorname{Im} f = \{ f(g)\in H\mid g\in G\} はそれぞれ G,H の部分群である。特に, \operatorname{Ker} f \subset G は正規部分群である。
- f が単射 \iff \operatorname{Ker} f = \{ e_G\}.
- f が同型なら,逆写像 f^{-1} も同型である。
- I が群, g\colon H\to I も準同型ならば,その合成 g\circ f\colon G\to I も準同型である。
1-2.は,「単位元」や「逆元の演算」も保たれると言っているわけですね。4.は単射であることの判定に非常に有効です。証明しておきましょう。
証明
1. f(e_G) = e_H について
f(e_G) = f(e_Ge_G)=f(e_G)f(e_G) より,両端辺 f(e_G)^{-1} をかけて e_H = f(e_G) である。
2. f(g^{-1}) = f(g)^{-1} について
f(g)f(g^{-1}) = f(gg^{-1})=f(e_G) = e_H より両端辺左から f(g)^{-1} をかけて f(g^{-1}) = f(g)^{-1} である。
3. \operatorname{Ker}f ,\operatorname{Im} f が部分群であることについて
G_0\subset G が部分群である必要十分条件は \color{red}a,b\in G_0\implies ab^{-1}\in G_0 が成り立つことであった(→部分群の定義と判定方法~例4つと性質~)。
a,b\in\operatorname{Ker} f とすると, f(ab^{-1}) = f(a)f(b^{-1}) = f(a)f(b)^{-1} = e_He_H^{-1} = e_H である。よって ab^{-1}\in \operatorname{Ker} f となるため, \operatorname{Ker} f は部分群である。
また,任意の a\in \operatorname{Ker} f ,\,g\in G に対し, f(gag^{-1})=f(g)f(a)f(g)^{-1} = f(g)f(g)^{-1} = e_H なので gag^{-1}\in \operatorname{Ker} f である。よって \operatorname{Ker} f は正規部分群である。
s,t\in \operatorname{Im} f とすると, f(a)=s, f(b)=t となる a,b\in G が存在する。 st^{-1} = f(a)f(b)^{-1} = f(a)f(b^{-1}) = f(ab^{-1}) なので, st^{-1}\in \operatorname{Im}f となり部分群である。
4. f が単射 \iff \operatorname{Ker} f = \{ e_G\} について
\implies は単射の定義より明らか。 \impliedby について, a,b\in G に対し, f(a)=f(b) を仮定すると, f(a)f(b)^{-1} = e_H である。すなわち f(ab^{-1})=e_H であり, ab^{-1}\in\operatorname{Ker} f = \{e_G\}. よって ab^{-1}=e_G となり, a=b. したがって f は単射である。
5. f が同型なら f^{-1} も同型について
s,t\in H に対し, a=f^{-1}(s), b=f^{-1}(t) とすると, f は同型より f(ab)=f(a)f(b) = st すなわち f^{-1}(st)=ab である。
f^{-1}(s)f^{-1}(t) = ab = f^{-1}(st) なので, f^{-1} は準同型であり,全単射なので同型である。
6. 準同型写像の合成も準同型写像であることについて
a,b\in G に対し, g(f(ab))=g(f(a)f(b)) = g(f(a))g(f(b)) より, g\circ f も準同型である。
証明終
なお,\operatorname{Im} f \subset H は正規部分群であるとは言えません。実際, G\subset H を正規部分群でない部分群とし, f\colon G\to H を包含写像とすると, f は準同型ですが, \operatorname{Im} f =G\subset H となり,これは正規部分群ではありません。
群の準同型の例
いくつか簡単な具体例を確認しておきましょう。
群の準同型の例1.
n 次正則行列(可逆行列)全体のなす群(一般線形群) \mathrm{GL}_n(\mathbb{R}) に対し,行列式(det)を返す写像
\color{red}\det \colon \mathrm{GL}_n(\mathbb{R}) \to \mathbb{R}^\times
は準同型写像である。ただし,\mathbb{R}^\times =\mathbb{R}\setminus\{0\} とした。とくに \det は全射であり,
である(特殊線形群という)。
\mathrm{GL}_n(\mathbb{R}),\mathbb{R}^\times は積に関して群になりますね。
\det (AB)=\det A\det B ですから(→行列式の性質6つの証明(列,行の線形性,置換,積,転置など)),群準同型です。
群の準同型の例2.
n 次対称群 S_n の各元 \sigma \in S_n に対し,その置換の符号 \operatorname{sgn} \sigma を返す写像
\color{red}\operatorname{sgn}\colon S_n \to \{\pm 1\}
は全射準同型写像である。ここで,
である( A_n は n 次交代群)。
とくに, n=2 のときは S_2=\{e, (12)\}, A_2=\{e\} であるから, \operatorname{sgn} は全単射となり,同型である。したがって, \color{red}S_2 \simeq \{\pm 1\} である。
S_2 と \{\pm 1\} は群として全く同じものと考えてよいということです。
環の準同型写像・同型写像
つづいて,環の間の準同型写像・同型写像を考えます。
以下で,環は零環(自明な環)でない,すなわち 0\ne 1 とします。また,環は単位的,すなわち乗法単位元 1 が存在するとします。
環準同型写像・同型写像の定義
定義2(環の準同型・同型)
R,S を環とする。 f\colon R\to S が
- \color{red} f(a+b) = f(a)+f(b) \quad (a,b\in R)
- \color{red} f(ab)=f(a)f(b) \quad (a,b\in R)
- \color{red} f(1_R) = 1_S
をみたすとき, f を環の準同型 (homomorphism) という。
さらに f が全単射なら環の同型 (isomorphism) といい,\color{red}R\simeq S や \color{red} R\cong S とかく。

環には和・積の2つの演算が入っていますから,その両方の演算を保つものを「準同型写像」というわけです。条件3.は零写像にならないことを保証します。特に, \operatorname{Ker} f \subsetneq R です( \operatorname{Ker}f の定義は定理2の中)。
環準同型写像の性質
定理2(環準同型の性質)
R,S を環とし, f\colon R\to S を環の準同型とする。このとき,
- f(0_R) = 0_S.
- a\in R に対し, f(-a) = -f(a) であり, a が単元であれば(逆元が存在すれば) f(a^{-1})=f(a)^{-1} も成り立つ。
- \operatorname{Ker} f =\{ a\in R\mid f(a)=0_R\}, \; \operatorname{Im} f = \{ f(a)\in S\mid a\in R\} はそれぞれ R,S の部分環である。特に, \operatorname{Ker} f \subset R は(両側)イデアルである。
- f が単射 \iff \operatorname{Ker} f = \{ 0_G\}.
- f が同型のとき,逆写像 f^{-1} も同型である。
- R が体のとき, f は単射である。
- T も環, g\colon S\to T も準同型であるとすると, g\circ f\colon R\to T も準同型である。
証明
1-5,7.については,群のときと同様なので省略する。
6. R が体のとき f が単射であること
3.より, \operatorname{Ker} f\subsetneq R はイデアルであるが,体は自明なイデアルしか持たないので, \operatorname{Ker} f=\{0_R\} である。4.より, f は単射である。
証明終
環の準同型の例
環の準同型の例1.
\mathbb{Z} は環である。 f(n)=-n とする写像
\color{red} f\colon \mathbb{Z}\to \mathbb{Z}
は環の同型写像である。
環の準同型になっていることは簡単に確認できますし,全単射は明らかですから, f は同型写像です。
環の準同型の例2.
R を環とし,
\color{red} f\colon \mathbb{Z}\ni n \mapsto \underbrace{1_R+\dots +1_R}_{n} \in R
とすると,これは環の準同型である。
環の準同型になっていることは確認してみてください。一般に,任意の零環でない環について,このような準同型が定まります。
環の準同型の例3.
実数係数1変数多項式全体の集合 \mathbb{R}[x] は環である。このとき,
\color{red}\phi \colon \mathbb{R}[x]\ni f(x) \mapsto f(\sqrt{-1}) \in \mathbb{C}
は環の準同型である。
和・積の計算をしてから x=\sqrt{-1} を代入するのと, x=\sqrt{-1} を代入してから和・積の計算をするのは同じになりますね。
体の準同型写像・同型写像
最後に,体の間の準同型写像・同型写像を定義します。
体準同型写像・同型写像の定義
体は環でもありますから,環と見ることで体の準同型が定義されます。
定義3(体の準同型・同型)
K,L を体とする。 f\colon K\to L が環としての準同型であるとき, f を体の準同型 (homomorphism) という。
さらに f が全単射なら体の同型 (isomorphism) といい,\color{red}K\simeq L や \color{red} K\cong L とかく。
今までの準同型の定義と比べて簡素に思うかもしれませんが,そもそも環から体では演算規則が増えたわけではないため,ある意味簡素なのは当然でしょう。
定理2.6で示したように,体の準同型は常に単射です。
体準同型写像の性質
定理3(体準同型の性質)
K,L を体とし, f\colon K\to L を体の準同型とする。このとき,
- f は常に単射である(→定理2.6)。
- f が同型ならば f^{-1} も同型である。
- M も体, g\colon L\to M も準同型とすると, g\circ f\colon K\to M も準同型である。
証明は同様なので省略します。
体の準同型の例
体の準同型の例1.
\mathbb{C} は体である。
\color{red} f\colon \mathbb{C} \ni z\mapsto \overline{z}\in \mathbb{C}
とすると,これは体の同型写像である。
\overline{z_1+z_2}=\overline{z_1}+\overline{z_2}, \overline{z_1z_2}=\overline{z_1}\,\overline{z_2} ですから,環の準同型であり, \mathbb{C} は体なので体の準同型ですね。全単射は明らかなので体の同型です。
準同型定理
上で挙げなかった性質で,特に大事なものが「準同型定理」と呼ばれるものです。基礎的な群論・環論の一つのゴールといえる大定理です。最も基本的な主張のみ記述しましょう。
定理(準同型定理)
A,B を群(または環)とし, f\colon A\to B を群の(または環の)準同型とする。このとき,
\large \color{red} A/\operatorname{Ker} f \simeq \operatorname{Im} f
が成り立つ。
左辺は剰余群(商群)(または剰余環(商環))です。体については, \operatorname {Ker} f=\{0\} になってしまいますから,あまり意味のない主張になってしまいます。
準同型定理について詳しくは,いずれ別の記事で解説しましょう。