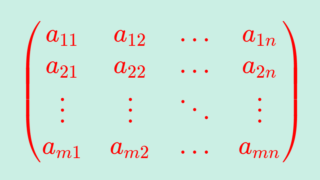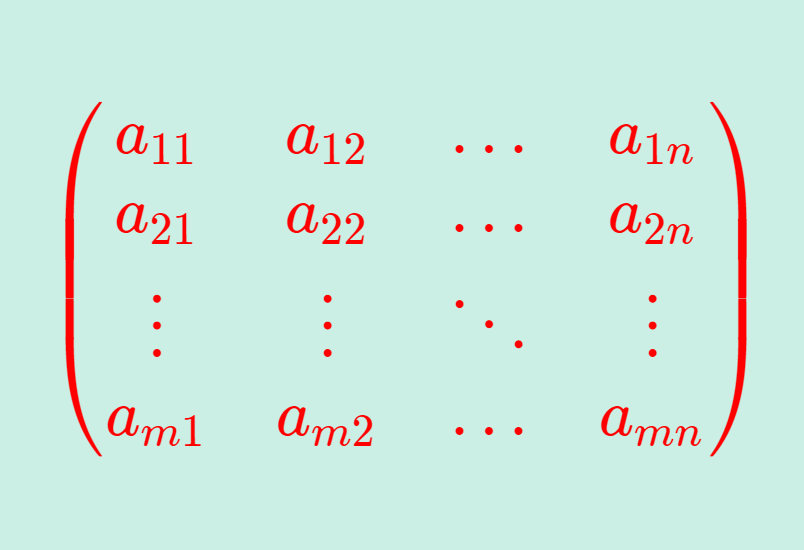べき零行列とは,行列のべき乗について,A^k=O (右辺は零行列)となるような行列のことです。
べき零行列の定義と例,そして性質について,順番に解説しましょう。
べき零行列の定義
定義(べき零行列)
A を n 次正方行列とする。ある正の整数 k が存在して,
\color{red} \large A^k=O
とできるとき, A をべき零行列(冪零行列; nilpotent matrix)という。
同じ行列のべき乗が,いずれ零行列になるものを,べき零行列というんですね。
べき零行列の具体例
べき零行列の具体例をチェックしていきましょう。
べき零行列の例1.
- A=\begin{pmatrix}0&1\\0&0\end{pmatrix} とすると,A^2=O.
- B = \begin{pmatrix} 3 & -1\\ 9& -3 \end{pmatrix} とすると,B^2=O.
- C=\begin{pmatrix}-2&2&2\\ -3&4&5\\2&-2&-2\end{pmatrix} とすると,C^2\ne O, \;C^3=O.
それぞれ具体的に確認してみてください。さらに,以下のような例も挙げましょう。
べき零行列の例2.
n 次正方行列 A が
A=\begin{pmatrix}0&1 &&&&&\huge{0} \\ & 0 & 1 \\ & & 0 & 1 \\ &&&\ddots & \ddots \\ &&&&\ddots & \ddots \\ &&&&&0 & 1 \\ \huge{0}&&&&&&0\end{pmatrix}
のとき, 1\le k\le n-1 に対して,
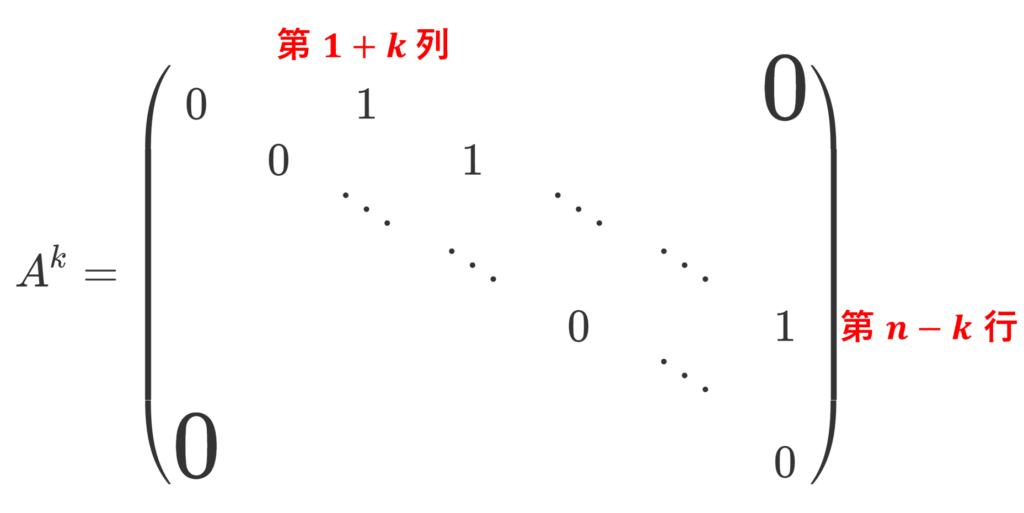
であり,A^n=O である。
これも,具体的に計算してみるのが良いでしょう。
より一般に,以下のような行列はべき零です。
べき零行列の例3.
対角成分がすべて 0 である三角行列はべき零である。
これについては,三角行列の固有値は対角成分そのものであることと,下の性質2.から従います。また逆に,三角行列がべき零であれば,対角成分は全て 0 でなければなりません。
べき零行列の性質7つとその証明
ここからは,べき零行列の重要な性質7つを紹介しましょう。
定理(べき零行列の性質)
A を n 次べき零行列とし, k をA^{k-1}\ne O, \; A^k=O (零行列)をみたす整数とする。このとき,
それぞれ証明していきましょう。
1. べき零行列が正則でないこと
1.の証明
一般の行列 U,V について, \det (UV)=\det U \det V が成立する(→行列式の性質6つの証明(列,行の線形性,置換,積,転置など))。
これより,
0 = \det O = \det (A^k) = (\det A)^k
であるから, \det A=0. ゆえに A は正則(可逆)でない。
証明終
2. べき零行列⇔固有値が0のみ
2.の証明
べき零行列 \implies 固有値が 0 のみについて
\lambda \in\mathbb{C} を A の固有値, \boldsymbol{x}\in \mathbb{C}^n \setminus\{\boldsymbol{0}\} をその固有ベクトルとする。このとき, A\boldsymbol{x}=\lambda \boldsymbol{x} であるから,
A^k \boldsymbol{x}= \lambda A^{k-1}\boldsymbol{x}=\dots = \lambda^k \boldsymbol{x}.
一方で, A^k=O であるから, \lambda^k=0. よって \lambda =0 であり,固有値は 0 のみである。
固有値が 0 のみ \implies べき零行列について
固有値が 0 のみと仮定すると,固有多項式は \lambda^n になる。よって,ケーリーハミルトンの定理より, A^n =O. したがって, A はべき零行列である。
証明終
3. べき零行列はk<=n乗で0になること
3.の証明
2.の証明の後半より, A^n =O. よって, A^{k-1}\ne O,\; A^k=O となる k は k\le n である。
証明終
4. べき零行列のトレースは0であること
5. べき零行列が対角化可能なら零行列であること
5.の証明
べき零行列 A が対角化可能であると仮定する。このとき,ある正則行列(可逆行列) P が存在して, D=P^{-1}AP とできる。ただし,D は対角行列である。
D の対角成分は固有値であり, D の固有値は A の固有値と一致しているから(→行列の相似とは~定義と性質6つの証明~),D=O である。よって,
A=PDP^{-1}=POP^{-1}=O.証明終
任意の正方行列は三角化可能ですが,三角行列においても,対角成分は固有値になるため,べき零行列を三角化すれば,その対角成分は 0 になります。
6. λI+A(λ≠0)が正則であること
6.の証明
性質2.より,固有多項式は \det(\lambda I_n -A) =\lambda^n である。よって, \lambda \ne 0 とすると, \det (\lambda I_n-A) \ne 0 である。
したがって, \lambda I_n -A は正則(可逆)であり, \lambda を -\lambda に置き換えることで \lambda I_n +A も正則(可逆)である。
証明終
7. AB=BAならA+B,ABもべき零行列であること
7.の証明
A,B を共にべき零行列とすると,性質3.より, A^n=B^n=O である。AB=BA とすると,
\begin{aligned}(AB)^n &= A^nB^n=O, \\ (A+B)^{2n} &=\sum_{k=0}^{2n} {}_{2n}\mathrm{C}_k\, A^{2n-k}B^k = O. \end{aligned}
よって, AB,A+B はべき零行列である。
証明終
注意ですが,AB\ne BA のとき,一般に A+B,AB はべき零行列になりません。たとえば,具体例1で紹介した2つの行列 A=\begin{pmatrix}0&1\\0&0\end{pmatrix},\; B = \begin{pmatrix} 3 & -1\\ 9& -3 \end{pmatrix} はどちらもべき零ですが,
\begin{aligned}A+B &= \begin{pmatrix} 3&0\\ 9&-3\end{pmatrix},\\ AB&= \begin{pmatrix} 9&-3\\0&0\end{pmatrix} \end{aligned}
はべき零ではありません。