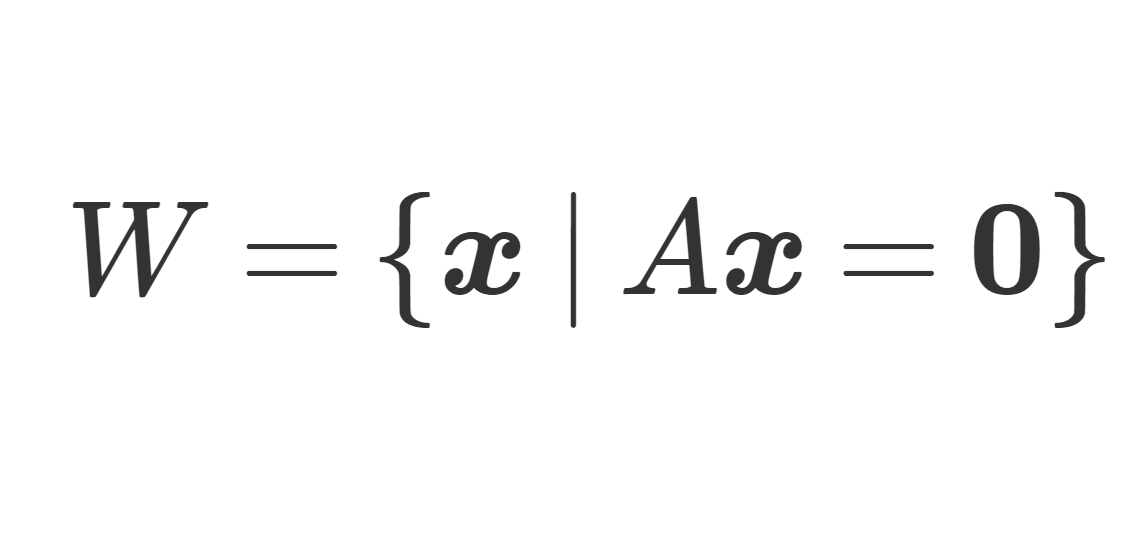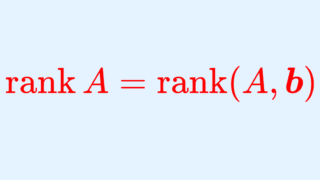連立一次方程式の基本解・特殊解と解空間の性質

連立一次方程式における，基本解・特殊解と解空間の定義とその性質について，理解しておくべき重要な定理を紹介し，証明しましょう。

連立一次方程式の基本解・特殊解と解空間
1. 連立一次方程式の基本解・解空間とは
2. 連立一次方程式の特殊解とは
基本解・特殊解・解空間の性質
1. 解空間の次元
2. Ax=b の全ての解
連立一次方程式と行列に関する記事

連立一次方程式の基本解・特殊解と解空間

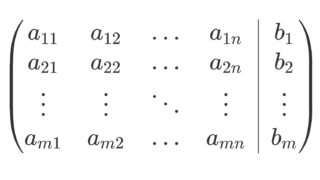
連立一次方程式

\begin{cases} a_{11}x_1+a_{12}x_2+\cdots + a_{1n}x_n = b_1 \\ a_{21}x_1+a_{22}x_2+\cdots + a_{2n}x_n = b_2 \\ \ldots \\ a_{m1}x_1+a_{m2}x_2+\cdots + a_{mn}x_n = b_m \end{cases}

は，行列を用いて表すと

\begin{pmatrix} a_{11} & a_{12} &\dots & a_{1n} \\ a_{21} & a_{22} &\dots & a_{2n} \\ \vdots & \vdots &\ddots & \vdots \\ a_{m1} & a_{m2}& \dots & a_{mn} \end{pmatrix}\begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{pmatrix} =\begin{pmatrix} b_1 \\b_2\\ \vdots \\ b_m \end{pmatrix}

とかけます。この式に対応して， $A\boldsymbol{x} = \boldsymbol{b}$ とかくことにしましょう。このときの $A$ を係数行列といいます(→係数行列・拡大係数行列とは)。

これを用いて，連立一次方程式の基本解・解空間・特殊解を定義します。

連立一次方程式の基本解・解空間とは

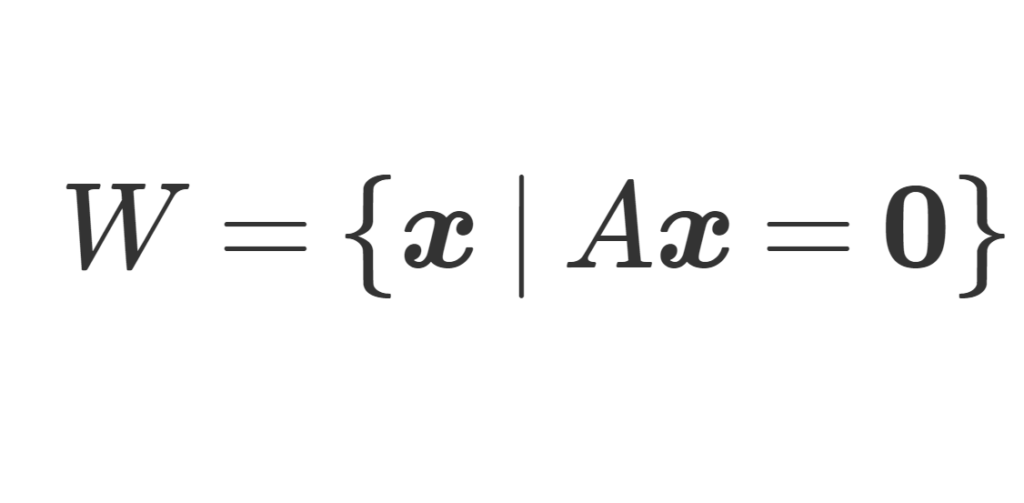
連立一次方程式 $A\boldsymbol{x} = \boldsymbol{b}$ に対して， $\boldsymbol{b}=\boldsymbol{0}$ とした連立一次方程式

A\boldsymbol{x} = \boldsymbol{0}

を斉次といいます。この，斉次連立一次方程式に関して，基本解と解空間が定義されます。

定義（基本解と解空間）

(右辺が $\boldsymbol{0}$ となる)斉次連立一次方程式 $A\boldsymbol{x} =\boldsymbol{0}$ の解 $\boldsymbol{x}\in\mathbb{C}^n$ の集合

\color{red} W = \{\boldsymbol{x} \mid A\boldsymbol{x} = \boldsymbol{0}\}

を解空間 (solution space) という。これは，ベクトル空間になる。また， $W$ の基底となる解を基本解 (fundamental solution) という。

$W$ は $\mathbb{C}^n$ の部分ベクトル空間です。実際，

\begin{gathered}\boldsymbol{x}, \boldsymbol{y} \in W \implies \boldsymbol{x}+\boldsymbol{y} \in W \\ \boldsymbol{x} \in W, k \in \mathbb{C} \implies k\boldsymbol{x} \in W \end{gathered}

となることからわかります。

ここで，もし $A$ が正則行列(可逆行列)ならば， $A\boldsymbol{x} = \boldsymbol{0}$ の両辺左から $A^{-1}$ をかけて $\boldsymbol{x}=A^{-1}\boldsymbol{0} = \boldsymbol{0}$ となります。すなわち， $\boldsymbol{x} =\boldsymbol{0}$ のみが解となります。これを，自明な解といい，「この斉次連立一次方程式は自明な解しか持たない」といいます。

連立一次方程式の特殊解とは

特殊解は，一般の連立一次方程式 $A\boldsymbol{x} = \boldsymbol{b}$ の「解の1つ」として定義されます。

定義（特殊解）

一般の連立一次方程式 $A\boldsymbol{x} = \boldsymbol{b}$ が解をもつとき，その解の任意の1つ $\boldsymbol{x'}$ を，その方程式の特殊解 (particular solution)という。

適当な解を一つだけ指して，特殊解というのですね。

そもそも，連立一次方程式 $A\boldsymbol{x} = \boldsymbol{b}$ が解をもつ必要十分条件は

\operatorname{rank} A = \operatorname{rank} (A, \boldsymbol{b})

ですが，今回は，連立一次方程式が解をもつものとして，先に進めます。

$\operatorname{rank} A = \operatorname{rank} (A, \boldsymbol{b})$ であることの詳細については，以下の記事で解説しています。

ここで，もし $A$ が正則行列(可逆行列)ならば， $A\boldsymbol{x} = \boldsymbol{b}$ の両辺左から $A^{-1}$ をかけて $\boldsymbol{x}=A^{-1}\boldsymbol{b}$ となります。すなわち， $\boldsymbol{x} = A^{-1}\boldsymbol{b}$ のみが解となり，特殊解は一つだけしかありません。