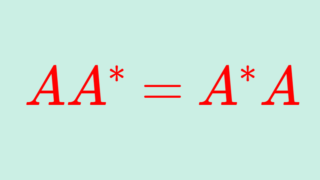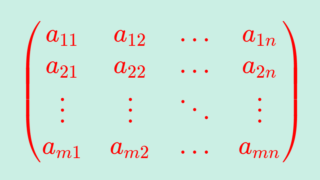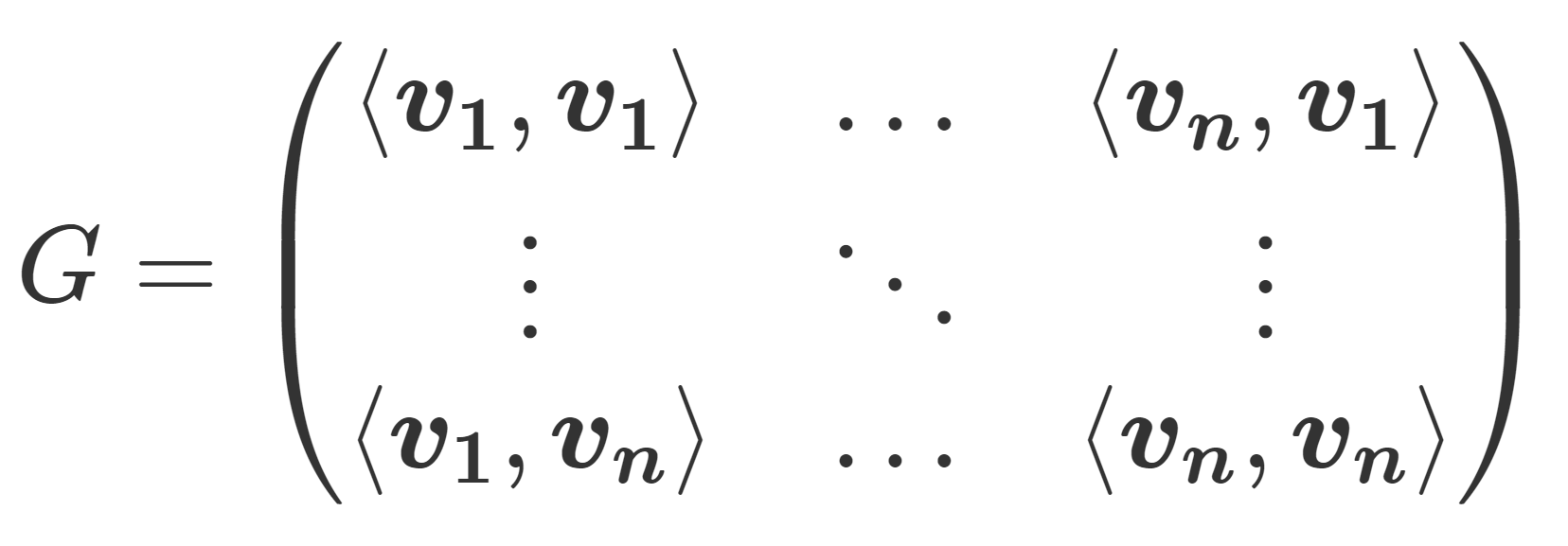正定値行列とは,内積について \langle A\boldsymbol{x}, \boldsymbol{x}\rangle>0 が成り立つ行列で,半正定値行列とは, \langle A\boldsymbol{x}, \boldsymbol{x}\rangle \ge 0 が成り立つ行列です。
正定値行列・半正定値行列について,その定義・性質を紹介しましょう。
正定値行列・半正定値行列
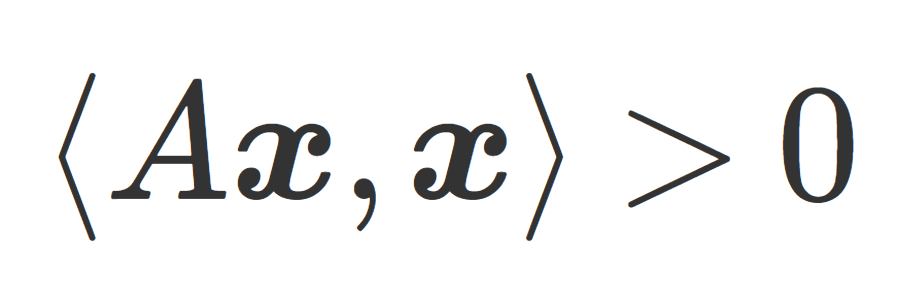
正定値行列・半正定値行列は,「実対称行列」またはより一般に「エルミート行列」に対して定義します。実対称行列・エルミート行列とはそれぞれ
A=A^\top ,\quad A=A^*
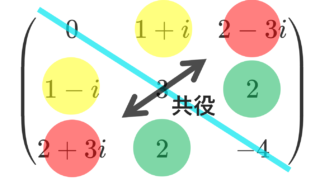
が成り立つ行列です。ただし, A^* = \overline{A}^\top は随伴行列(共役転置)です。実行列のときは, A^*=A^\top ですから,エルミート行列は対称行列になります。
定義(正定値行列・半正定値行列)
A を n 次実対称行列(あるいはエルミート行列)とする。任意の列ベクトル \boldsymbol{x}\in\mathbb{R}^n\setminus\{\boldsymbol{0}\}(あるいは \mathbb{C}^n \setminus\{\boldsymbol{0}\} )に対し,内積
\Large \color{red} \langle A \boldsymbol{x}, \boldsymbol{x} \rangle >0
が成立するとき, A を正定値行列 (positive definite matrix) という。また,
が成立するとき, A を半正定値行列 (positive semidefinite matrix) という。
\boldsymbol{x}= \begin{pmatrix}x_1\\ \vdots \\ x_n \end{pmatrix}, \boldsymbol{y} = \begin{pmatrix}y_1\\ \vdots \\ y_n \end{pmatrix} の内積について,実のときは \langle \boldsymbol{x}, \boldsymbol{y}\rangle = \boldsymbol{y}^\top \boldsymbol{x} = \sum_{k=1}^n x_ky_k ですから,実のときの正定値行列は
\color{red} \Large \boldsymbol{x}^\top A\boldsymbol{x}>0
と定義しても同じです。複素のときの内積は \langle \boldsymbol{x}, \boldsymbol{y}\rangle = \boldsymbol{y}^* \boldsymbol{x} = \sum_{k=1}^n x_k\overline{y}_k ですから,複素のときの正定値行列は
と定義しても同じです。
正定値行列・半正定値行列とは,二次形式と密接な関係がある概念です。二次形式については,別に解説しましょう。
正定値行列・半正定値行列の性質3つ
エルミート行列は実対称行列も含みますから,以下ではエルミート行列としましょう。
定理(正定値行列・半正定値行列の性質)
A を n 次エルミート行列とする。このとき,
証明の前に準備をしましょう。
1-3.の証明で用いる知識
エルミート行列は A=A^* ですから,特に AA^* =A^* A が成立します。よって正規行列です。以下の証明には,正規行列がユニタリ行列を用いて対角化可能であることを用います。すなわち,ユニタリ行列 U が存在して, D = U^{-1}AU を対角行列にできます。このとき,
D= \begin{pmatrix} \lambda_{1} \\ & \lambda_{2} && \huge{0} \\ & & \ddots \\ &\huge{0}&& \ddots \\ &&&& \lambda_{n} \end{pmatrix}
としましょう。\lambda_1, \lambda_2, \dots, \lambda_n は行列 A,D の固有値になります(→行列の相似とは~定義と性質6つの証明~)。
この記号を用いて,証明をしていきましょう。
1. 正定値行列(半正定値行列)⇔固有値が正(非負)の実数
証明
正定値行列 \implies 固有値が正について
A の固有値を \lambda ,その固有ベクトルを \boldsymbol{x} とすると,
\langle A\boldsymbol{x}, \boldsymbol{x}\rangle = \langle \lambda \boldsymbol{x}, \boldsymbol{x}\rangle = \lambda \lVert \boldsymbol{x} \rVert^2
なので, A が正定値なら \lambda > 0 であり,半正定値なら \lambda \ge 0 である。
固有値が正 \implies 正定値行列について
\lambda_1, \lambda_2,\dots, \lambda_n >0 とする。このとき,任意の \boldsymbol{x}\in\mathbb{C}^n \setminus \{\boldsymbol{0}\} に対して \boldsymbol{y} =\boldsymbol{U}^* \boldsymbol{x} とする。ユニタリ行列は U^{-1}=U^* であることに注意して,
\boldsymbol{x}^* A\boldsymbol{x}= \boldsymbol{x}^* UDU^{-1} \boldsymbol{x} = \boldsymbol{x}^* UDU^{*} \boldsymbol{x} = \boldsymbol{y}^* D \boldsymbol{y}
である。 \boldsymbol{y} = \begin{pmatrix}y_1\\ \vdots \\ y_n \end{pmatrix} とすると,
であり, 結局 \boldsymbol{x}^* A\boldsymbol{x} >0 なので A は正定値行列である。半正定値行列であることの証明も同様である。
証明終
なお,エルミート行列の固有値はそもそも実数になることが知られています。
2. 半正定値行列⇔グラム行列
証明
半正定値行列 \implies グラム行列について
1.より, \lambda_1, \lambda_2, \dots \lambda_n\ge 0 である。行列 \sqrt{D} を
\sqrt{D} = \begin{pmatrix} \sqrt{\lambda_{1}} \\ &\sqrt{ \lambda_{2}} && \huge{0} \\ & & \ddots \\ &\huge{0}&& \ddots \\ &&&& \sqrt{\lambda_{n}} \end{pmatrix}
と定めると,
である。ここで, B = \sqrt{D}U^{-1} = \sqrt{D} U^* とすると, B^* = U \sqrt{D} であるから, A=B^*B である。よって, A はグラム行列である。
グラム行列 \implies 半正定値行列について
A=B^*B をグラム行列とする。一般に n 次正方行列 A とベクトル \boldsymbol{x},\boldsymbol{y}\in\mathbb{C}^n に対し, \langle A\boldsymbol{x}, \boldsymbol{y}\rangle = \langle \boldsymbol{x}, A^* \boldsymbol{y} \rangle が成り立つことに注意する(→随伴行列(エルミート転置,共役転置)の定義と性質10個)と,任意の \boldsymbol{x} に対して
\begin{aligned} \langle A\boldsymbol{x}, \boldsymbol{x}\rangle &= \langle B^*B\boldsymbol{x},\boldsymbol{x}\rangle = \langle B\boldsymbol{x},B\boldsymbol{x} \rangle \\&= \lVert B\boldsymbol{x} \rVert^2\ge 0 \end{aligned}
よって A は半正定値行列である。
証明終
3. 正定値行列は正則で逆行列も正定値行列
証明
1.より, \lambda_1,\lambda_2,\dots, \lambda_n>0 である。特に, D は正則(可逆)で,
D^{-1} = \begin{pmatrix} \lambda_{1}^{-1} \\ & \lambda_{2}^{-1} && \huge{0} \\ & & \ddots \\ &\huge{0}&& \ddots \\ &&&& \lambda_{n}^{-1} \end{pmatrix}
となる。このとき, UD^{-1}U^{-1} = (UDU^{-1})^{-1} = A^{-1} より, A は正則(可逆)で,固有値は \lambda_1^{-1}, \dots, \lambda_n^{-1}>0 となる。
(A^{-1})^* = (A^*)^{-1} = A^{-1} なので(→随伴行列(エルミート転置,共役転置)の定義と性質10個), A^{-1} もエルミート行列である。 A^{-1} の固有値が正なので,1.より,これは正定値行列である。
証明終