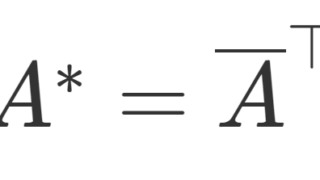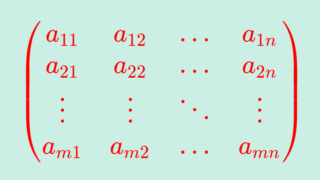行列における，その行と列を入れ替えた「転置行列」について，定義と，その基本的な性質を証明付きで紹介します。
転置行列の定義
定義（転置行列）
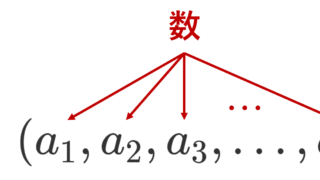
m \times n 行列
A = \begin{pmatrix} a_{11} & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} & \ldots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \ldots & a_{mn} \end{pmatrix}
に対し，その行と列を入れ替えた \color{red} n \times m 行列
を A の転置行列 (transposed matrix) という。 A の転置行列は， \color{red} A^\top, A^t, {}^t\!A, {}^\top\!A, A^{\mathrm{tr}}, A^{\prime} などと書かれることが多い。
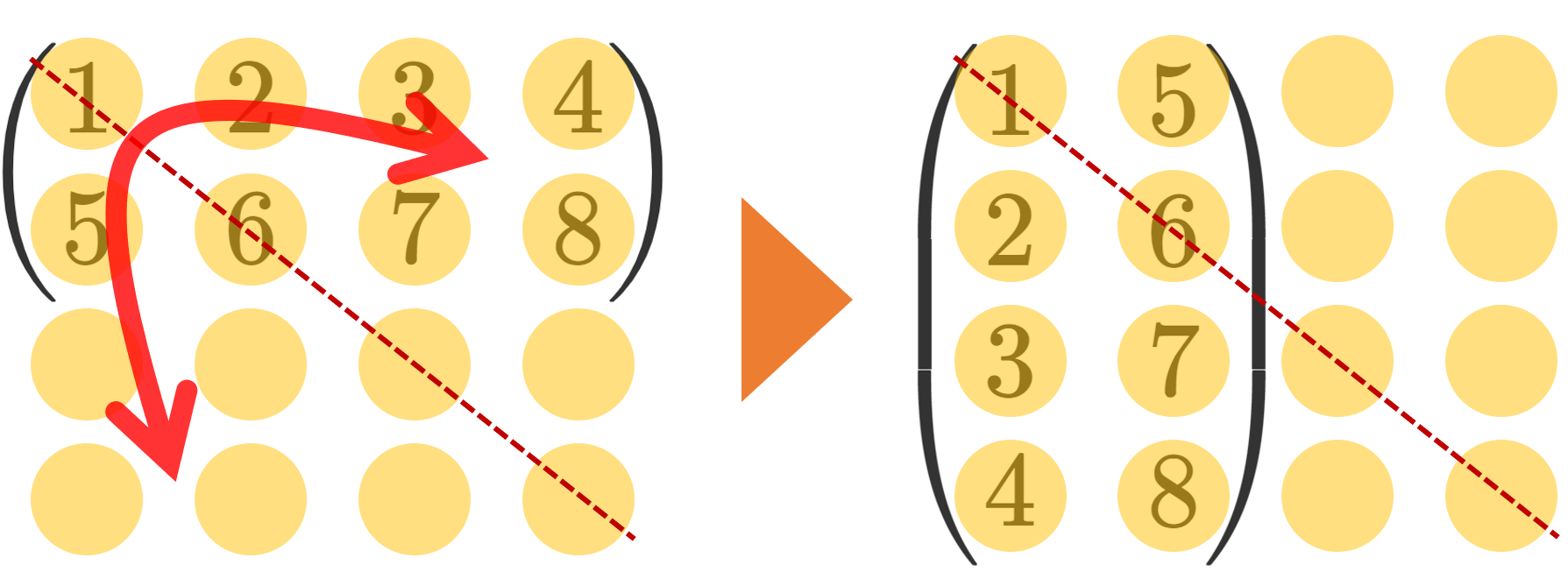
「行と列の入れ替え」とは， (i,j) 成分の値を (j,i) 成分に移すことです。イメージを図にすると，以下のような感じです。
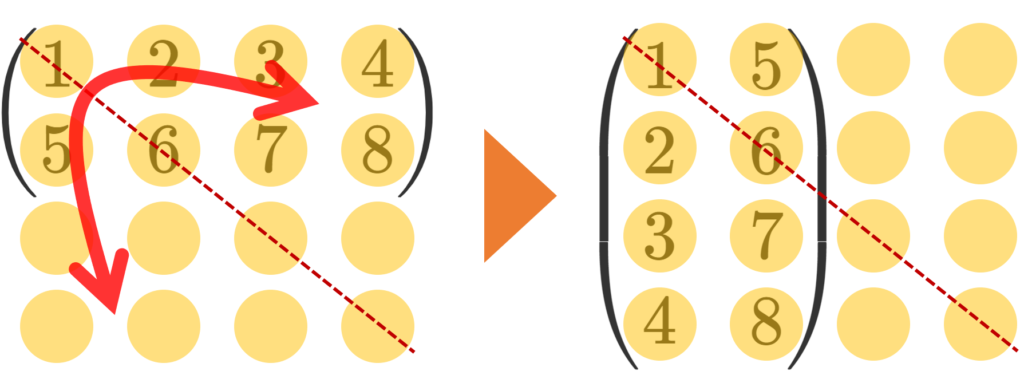
転置行列は，さまざまな書き方をしますが，一般に \color{red} A^\top, {}^t\!A のどちらかが多いです。
転置行列の具体例
いくつか具体例を挙げましょう。
転置行列の例
- {\begin{pmatrix} 1 & 2 & 3& 4 \end{pmatrix}}^\top = \begin{pmatrix} 1 \\ 2 \\ 3\\ 4 \end{pmatrix}.
- {\begin{pmatrix} 1& 2 \\ 3 & 4 \end{pmatrix}}^\top = \begin{pmatrix} 1 & 3 \\ 2 & 4 \end{pmatrix}.
- {\begin{pmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{pmatrix}}^\top = \begin{pmatrix} 1 & 3 & 5 \\ 2 & 4 & 6 \end{pmatrix} .
また， \mathbb{R}^n におけるベクトルの内積は，転置行列を用いた積で記述できます。
ベクトルの内積と転置行列
\boldsymbol{a}, \boldsymbol{b} \in \mathbb{R}^n を列ベクトルとする。すなわち，
\boldsymbol{a} = \begin{pmatrix} a_1 \\ a_2 \\ \vdots \\a_n \end{pmatrix} , \boldsymbol{b} = \begin{pmatrix} b_1 \\ b_2 \\ \vdots \\b_n \end{pmatrix}
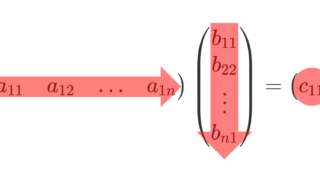
と書けるとする。このとき，この内積 \langle\boldsymbol{a} , \boldsymbol{b}\rangle は，各々を n\times 1 行列とみることで
とかける。
実際，両辺とも a_1b_1 + a_2b_2+\dots + a_n b_n となるので，正しいですね。
\mathbb{R}^n におけるベクトル(数ベクトル)は以下で解説しています。
行列の積に関しては，以下の記事を参照してください。
転置行列の基本的な性質11個
ここからは，一般の行列における転置行列の性質・正方行列における転置行列の性質をそれぞれ挙げ，証明しましょう。
一般の行列に対する転置行列の基本的な性質5つ
定理（転置行列の基本的な性質）
A, B を m \times n 行列とする。このとき，
- (A^\top)^\top = A.
- (A + B)^\top = A^\top + B^\top.
- (kA)^\top = k A^\top, ただし k は定数。
- C を対角行列とすると， C^\top = C .
また， A を m \times n 行列， B を n \times l 行列とすると，
- (AB)^\top = B^\top A^\top .
上4つはほぼ明らかでしょう。最後の式 (AB)^\top = B^\top A^\top だけ証明の概略を述べましょう。
(AB)^\top = B^\top A^\top の略証
A = (a_{ij}), B=(b_{ij}), A^\top = (a_{ij}^\prime) ,B^\top = (b_{ij}^\prime) と定めると， a_{ij}^\prime = a_{ji}, b_{ij}^\prime = b_{ji} である。
さらに， C = (c_{ij})= AB, C^\prime = (c_{ij}^\prime) = B^\top A^\top と定めると，
であるから， c_{ij}^\prime = c_{ji} なため， C^\top = C^\prime すなわち (AB)^\top = B^\top A^\top が従う。
略証終
もっと正確に証明するときは， i,j の範囲を明示すべきでしょう。
正方行列に対する転置行列の基本的な性質6つ
正方行列に関しては，以下のような性質があります。
定理（転置行列の基本的な性質2）
A を n 次正方行列とする。このとき，
- \operatorname{tr} A = \operatorname{tr} A^\top. (トレース)
- \det A = \det A^\top . (行列式)
- 転置行列の固有値は，元の行列の固有値と等しい。
- \operatorname{rank} A = \operatorname{rank} A^\top . (ランク)
- A を実正方行列とすると，列ベクトル \boldsymbol{v} , \boldsymbol{w} \in \mathbb{R}^n の内積について，
\langle A\boldsymbol{v}, \boldsymbol{w}\rangle = \langle \boldsymbol{v} , A^\top \boldsymbol{w} \rangle. - A を正則(可逆行列)とすると，
(A^\top)^{-1} = (A^{-1})^\top.
3.で「実」にした理由は，複素数の場合は，内積の定義が異なるからです。
それぞれを証明しておきましょう。
証明
1. \operatorname{tr} A = \operatorname{tr} A^\top について
\operatorname{tr} A = \sum_{k=1}^n a_{kk} = \operatorname{tr} A^\top から従う。
2. \det A = \det A^\top について
\begin{aligned} \det A &= \sum_{\sigma\in S_n} (\operatorname{sgn}\sigma) a_{1\sigma(1)}a_{2\sigma(2)}\dots a_{n\sigma(n)}, \\ \det A^\top &= \sum_{\sigma\in S_n} (\operatorname{sgn}\sigma) a_{\sigma(1)1}a_{\sigma(2)2}\dots a_{\sigma(n)n}\\ \end{aligned}
である(→行列式(det)の定義と現実的な求め方～計算の手順～)。ここで，第2式の右辺を，最初の添え字に対して昇順に並び替えると，
であることが分かる。 \operatorname{sgn} \sigma = \operatorname{sgn} \sigma^{-1} であるから，結局，
となって \det A^\top = \det A.
3. 転置行列の固有値は，元の行列の固有値と等しいことについて
\begin{aligned} \det (\lambda I - A) &= \det (\lambda I - A)^\top \\ &= \det(\lambda I - A^\top ) \end{aligned}
よりわかる(→固有値の定義と求め方をていねいに～計算の手順～)。
4. \operatorname{rank} A = \operatorname{rank} A^\top について
各列ベクトルに対する一次独立なものの個数と，各行ベクトルに対する一次独立なものの個数は等しく，これは階数 (rank) に一致していることから従う。
5. \langle A\boldsymbol{v}, \boldsymbol{w}\rangle = \langle \boldsymbol{v} , A^\top \boldsymbol{w} \rangle について
\begin{aligned}\langle A\boldsymbol{v}, \boldsymbol{w}\rangle &=\sum_{i=1}^n \left( \sum_{k=1}^n a_{ik}v_k\right) w_i \\ &=\sum_{i=1}^n \sum_{k=1}^n a_{ik}v_kw_i \\ & = \sum_{k=1}^n \sum_{i=1}^n a_{ik}v_kw_i \\ &=\sum_{k=1}^n v_k\left(\sum_{i=1}^n a_{ik} w_i\right) \\ &=\langle \boldsymbol{v} , A^\top \boldsymbol{w} \rangle. \end{aligned}
6. (A^\top)^{-1} = (A^{-1})^\top について
先ほど略証した (AB)^\top = B^\top A^\top を用いる。 I_n を n 次単位行列とすると，
\begin{gathered} (A^{-1})^\top A^\top = (A A^{-1})^\top = I_n , \\ A^\top (A^{-1})^\top = (A^{-1} A)^\top = I_n \end{gathered}
となり，これは (A^\top)^{-1} =(A^{-1})^\top を意味する。
証明終
無事にすべて証明できました。
