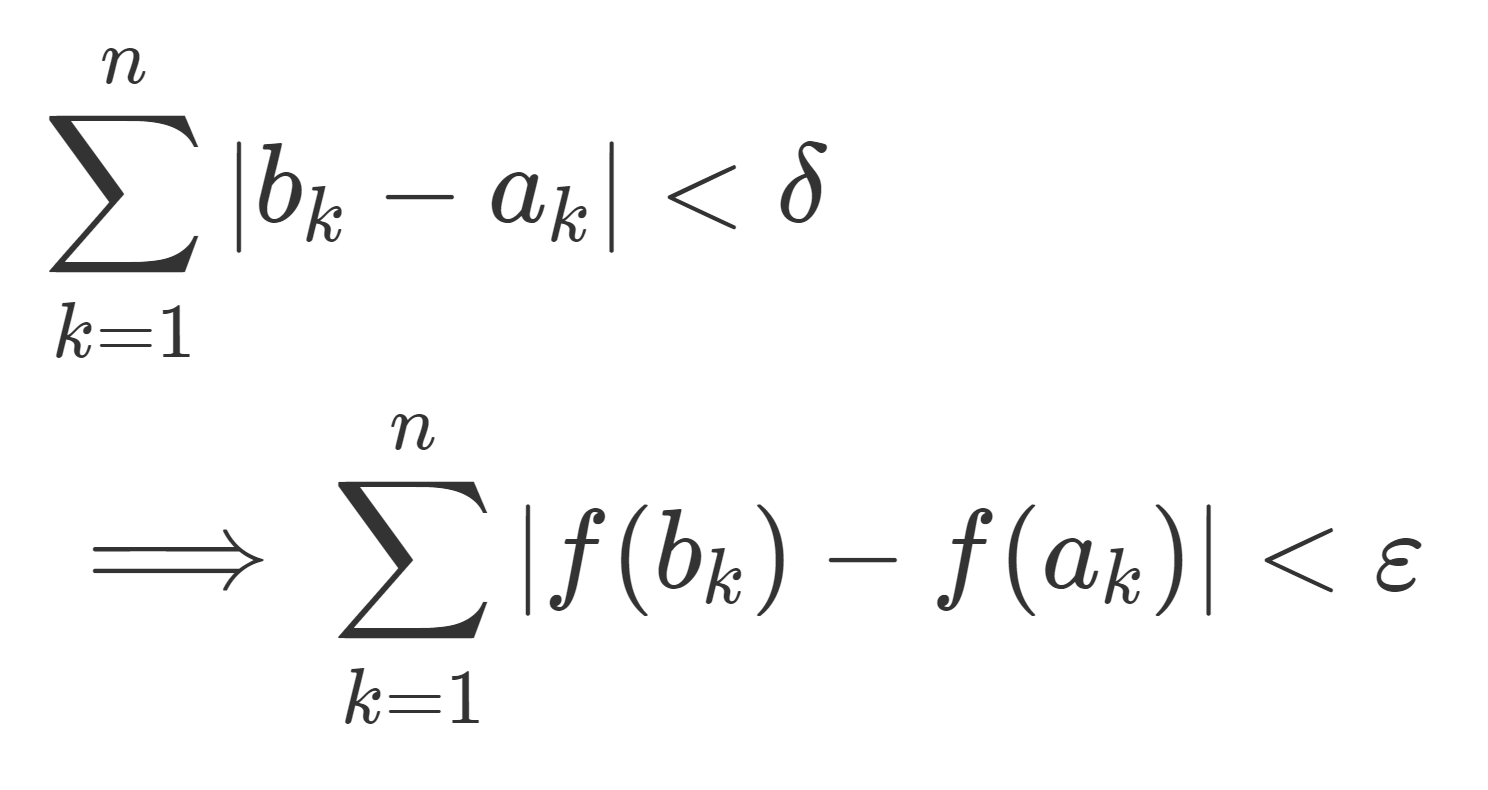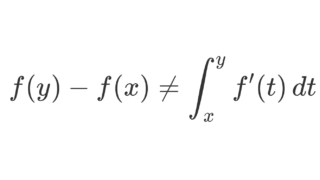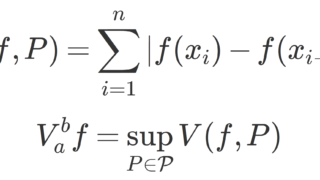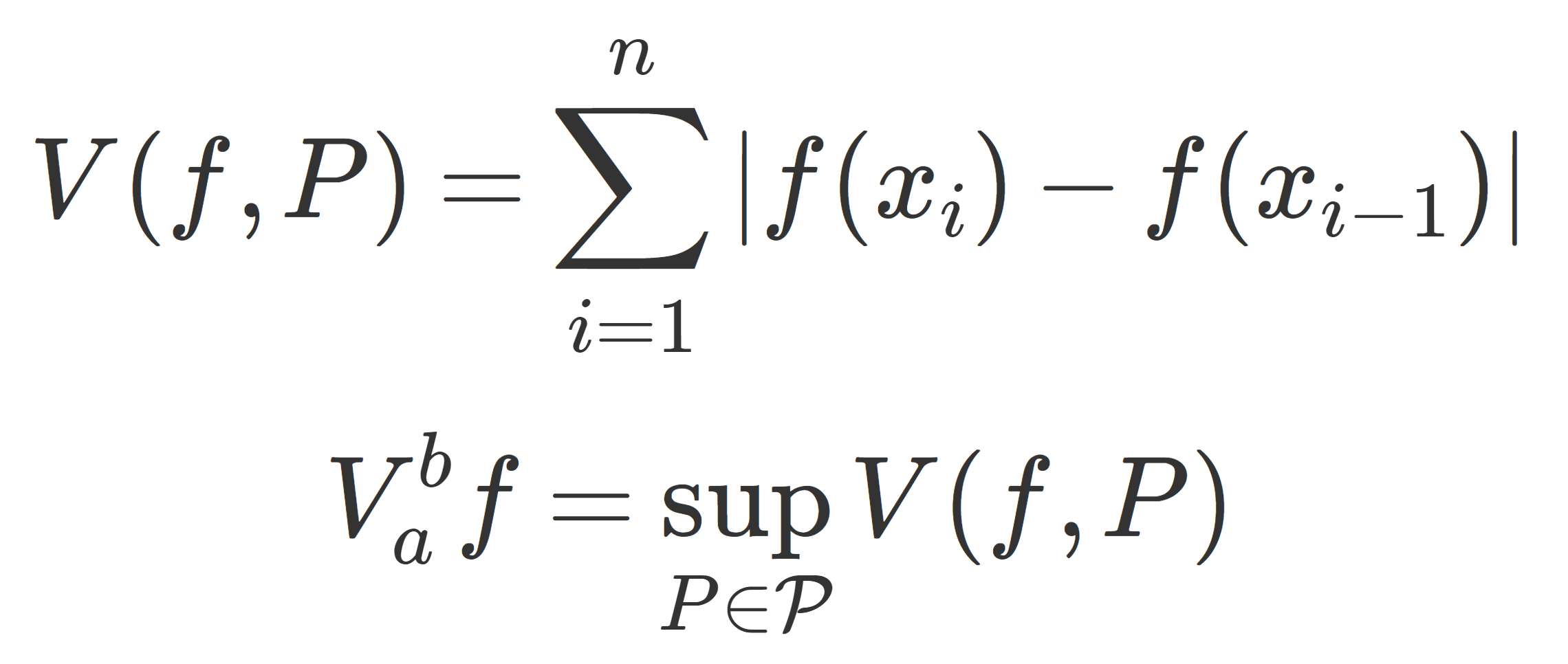絶対連続な関数とは,どの二つも共通部分を持たない任意の開集合族 \{( a_k, b_k)\} に対し,
\begin{aligned}&\sum_{k=1}^n |b_k-a_k|<\delta \\&\implies \sum_{k=1}^n |f(b_k)-f(a_k)|<\varepsilon \end{aligned}
が成り立つことを言います。一様連続の定義をさらに厳しくしたような感じです。関数が絶対連続であることは,ほとんどいたるところ微分可能で,
が成り立つことと同値です。また,測度の絶対連続性の概念とも密接に関連しています。
絶対連続性について,その定義・例・性質を紹介しましょう。
絶対連続な関数とは
定義(絶対連続関数)
I\subset \R を区間とする。関数 f\colon I\to \R が絶対連続 (absolutely continuous) であるとは,
任意の \varepsilon >0 に対し,ある \delta>0 が存在して,どの二つも共通部分を持たない任意の開集合族 \{( a_k, b_k)\} に対し,
\large \color{red} \begin{aligned}&\sum_{k=1}^n |b_k-a_k|<\delta \\&\implies \sum_{k=1}^n |f(b_k)-f(a_k)|<\varepsilon \end{aligned}
が成り立つことをいう。
I は [a,b] でも \R とかでもよいです。
定義より特に |b-a|<\delta \implies |f(b)-f(a)|<\varepsilon が成り立ちます。これは一様連続の定義ですから,絶対連続関数は一様連続です。
絶対連続な関数の例・そうでない例
絶対連続な例・そうでない例1.
f(x)=x^2 \; (-1\le x\le 1) は絶対連続であるが, g(x)=x^2\; (x\in \R) は絶対連続でない。
任意の x, y\in [-1,1] に対し, |f(x)-f(y)|\le 2|x-y| が成り立つので, f は絶対連続ですが, g は |g(x+\delta)-g(x)|\xrightarrow{x\to\infty} \infty であることから,絶対連続ではありません。特に, g は一様連続でもありません。
絶対連続な例2.
f(x)=\sin x \; (x\in \R) は絶対連続である。
任意の x, y\in \R に対し, |f(x)-f(y)|\le |x-y| が成り立つので, f は絶対連続ですね。
絶対連続でない例2.
f(x)=\begin{cases} x \cos (\pi /x) & 0<x\le 1 ,\\ 0 & x=0\end{cases} は,閉区間 [0,1] 上連続なので一様連続だが,絶対連続ではない。
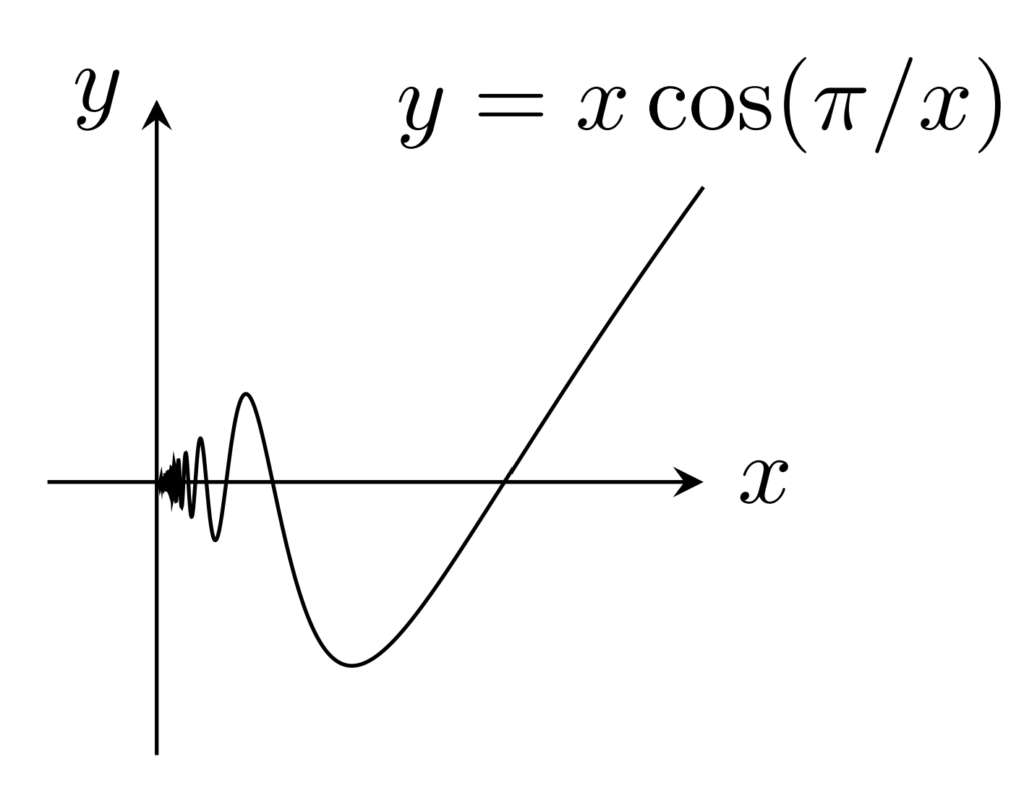
閉区間上連続ならば一様連続なので,一様連続であることはよいです。一方で, x_n = 1/n とすると,任意の \delta>0 に対して, N\ge 1 を十分大きくすることで,
\sum_{n=N}^\infty |x_{n+1}-x_n|= \frac{1}{N}<\delta
とできますが,
となってしまって絶対連続ではありません。
絶対連続でない例3.
カントール関数は絶対連続でない。
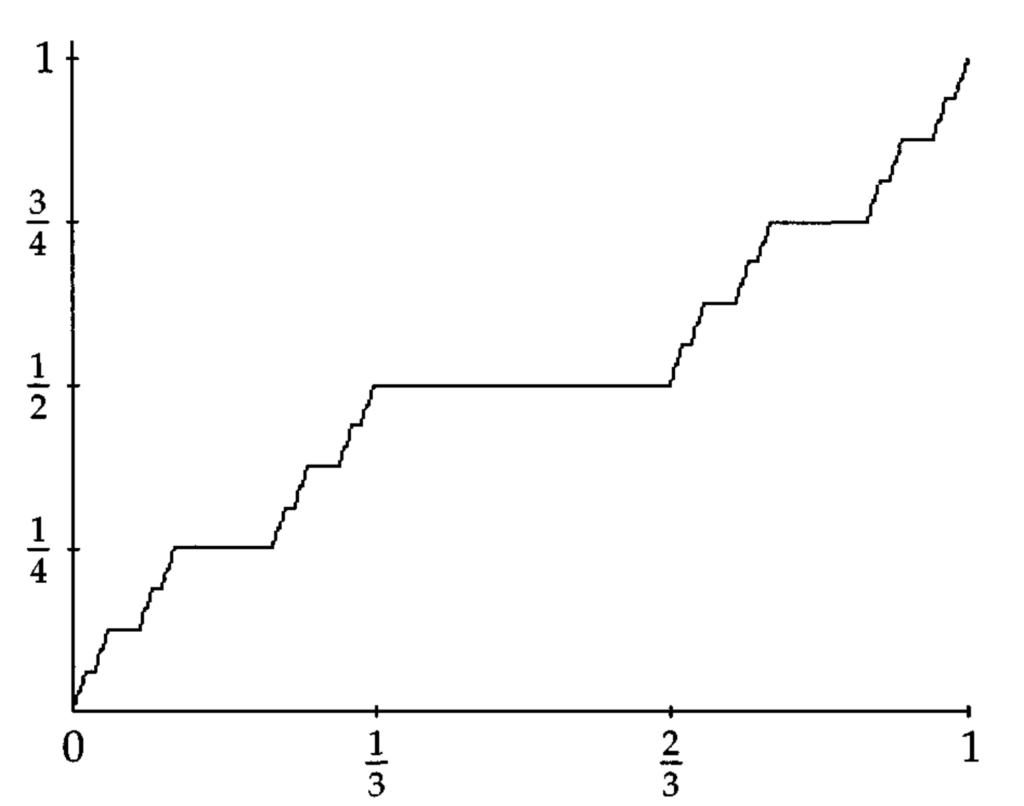
悪魔の階段とも呼ばれるカントール関数ですが,これは絶対連続ではありません。ただ,閉区間上連続なので,一様連続ではあります。
絶対連続な関数の性質
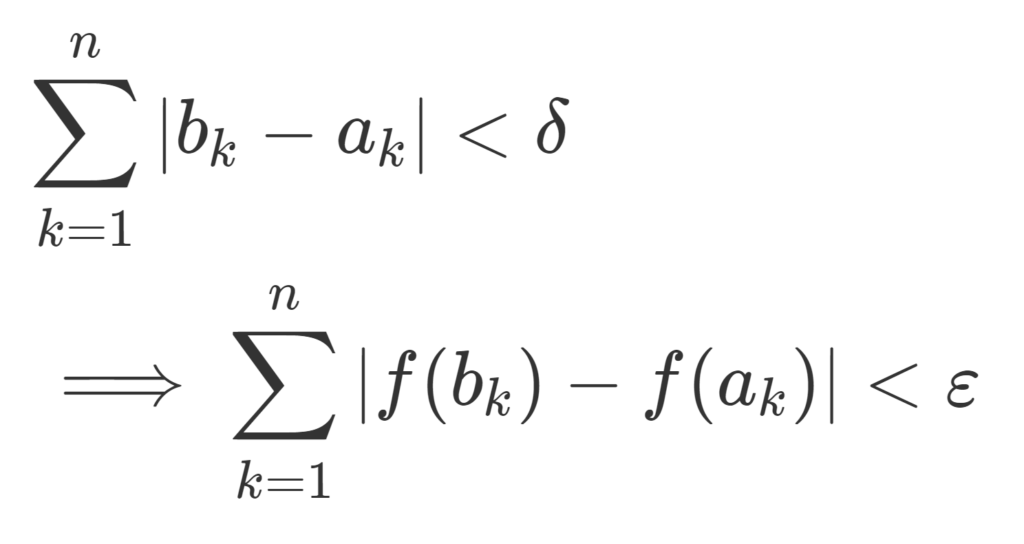
定理の直後に,「絶対連続なら一様連続」と述べました。ここからは,それ以外の性質を紹介していきましょう。
以下では, I\subset \R とします。
1. 絶対連続関数は零集合を零集合にうつす
定理1(絶対連続関数は零集合を零集合にうつす)
関数 f\colon I\to \R を絶対連続とする。このとき,N\subset I を(ルベーグ測度に関する)零集合とすると,像 f(N) も零集合である。
測度にも絶対連続という概念があります。その定義は,以下のようなものです。
詳しくは測度の絶対連続性・同値性・特異性とルベーグ分解で解説しています。測度の絶対連続性と,関数の絶対連続性は定義に関連性がないように見えるかもしれませんが,定理1を通して,類似した概念であることがわかるのではないでしょうか。
定理1を証明しておきましょう。
証明
まず f を広義単調増加関数として示す。
以下,m をルベーグ測度とする。 N\subset I を零集合(すなわち m(N)=0)とする。 N は区間 I の端点を含まないとしてよい。\varepsilon >0 とし, \delta>0 を 絶対連続関数 f の定義をみたすものとして取る。
ルベーグ測度の外部正則性より,ある開集合 N\subset V\subset I が存在して, m(V)<\delta とできる。 \{(a_k, b_k)\} を互いに素な開区間であって, \bigcup_k (a_k, b_k)= V となるように取る(無限個でも良い)。このとき,\sum_k (b_k-a_k) <\delta であり,絶対連続性より,
\sum_k ( f(b_k)-f(a_k))\le \varepsilon .
f は広義単調増加より, f(N)\subset \bigcup_{k} [f(a_k), f(b_k)] であるため, f(N) は任意に小さいボレル集合の部分集合となる。ルベーグ測度は完備なので, f(N) はルベーグ可測で, m(f(N))=0 といえる。
f が一般の関数のとき,
以下の定理2.の証明の後で述べるように,絶対連続関数は絶対連続な広義単調増加関数の差としてかける。そこで, f=p-n とする。ルベーグ測度の平行移動不変性より,(実際はルベーグ測度の完備性より f(N) がルベーグ可測であることを示した後で)
m(f(N))\le m(p(N))+m(n(N))=0
となってよい。
証明終
2. 絶対連続関数は有界変動である
定義域が [a,b] であることに注意してください。たとえば, f\colon \R\to\R を y=\sin x とすると,これは絶対連続ですが,有界変動ではありません。ただし,局所有界変動,すなわちコンパクト集合上有界変動ではあります。
有界変動の定義を復習しておきましょう。
P=\{ \{x_n\}\mid a=x_0<x_1<\dots< x_n=b\} を(有限)分割とし,(有限)分割全体の集合を \mathcal{P} とする。
f\colon [a,b]\to\R が有界変動 (bounded variation) とは,
\sup_{P\in\mathcal{P}} \sum_{k} |f(x_{k})-f(x_{k-1})|<\infty
が成り立つことを言う。左辺を V_a^b f と表し,全変動 (total variation) という。
詳しくは有界変動関数の定義と例といくつかの大事な性質で解説しています。
証明
絶対連続の定義より, \delta >0 が存在して,どの2つも互いに素な任意の開区間族 \{(a_k, b_k)\} に対し,
\begin{aligned}&\sum_{k=1}^n |b_k-a_k|\le \delta \\&\implies \sum_{k=1}^n |f(b_k)-f(a_k)|\le 1 \end{aligned}
とできる。分割 P=\{ \{x_n\}\mid a=x_0<x_1<\dots< x_{\lceil(b-a)/\delta\rceil}=b\} を, |x_k-x_{k-1}|<\delta をみたすように取る( \lceil\cdot \rceil は天井関数)。このとき, [x_{k-1}, x_k] 間をさらに分割して x_{k-1}=y_0<y_1<\dots< y_m=x_k とする。 \sum_{j=1}^m |y_{j}-y_{j-1}| = x_k-x_{k-1}<\delta より,絶対連続の定義から,
となる。したがって, P からさらに分割した任意の分割 \{z_l\} について
とできる。ゆえに,
なので,示された。
証明終
注意ですが,逆は成り立ちません。つまり,有界変動だからといって,絶対連続にはなりません。単調関数は有界変動なので,カントール関数は有界変動ですが,絶対連続ではありませんでしたね。
絶対連続関数は有界変動なので,有界変動関数がみたす全ての性質をみたすことになります。たとえば,絶対連続関数は2つの広義単調増加関数の差でかけます。特に絶対連続関数の場合は,2つの広義単調増加関数も絶対連続になります。これは,
- [a,x] 間の全変動 v(x)=V_a^x f が絶対連続であることと,
- 有界変動関数が2つの広義単調増加関数の差でかける証明で与えた広義単調増加関数の形と,
- 絶対連続の関数の和も絶対連続である(以下の定理4)
ことからわかります。 v(x) が絶対連続であることは,絶対連続の定義を考えればすぐ示せるので,省略します。
3. 絶対連続関数はほとんどいたるところ微分可能
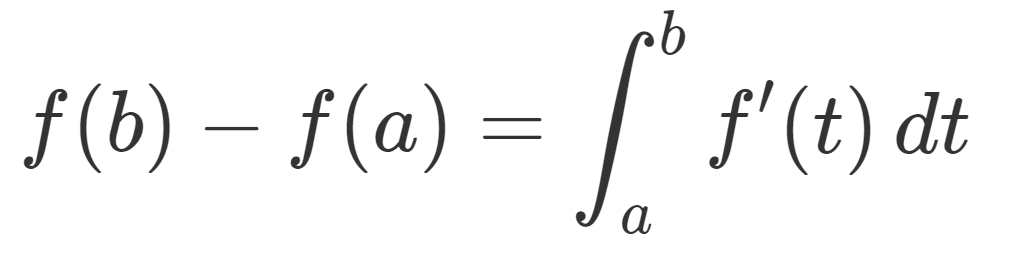
定理3(絶対連続ならほとんどいたるところ微分可能)
f\colon I\to \R が絶対連続なら,ほとんどいたるところ微分可能である。さらに, (a,b)\subset I とすると,
\color{red} f(b)-f(a)=\int_a^b f'(t)\, dt
となる。
絶対連続でなくとも,有界変動であればほとんどいたるところ微分可能です。しかし絶対連続でない場合には,一般には赤字の式は成立しません。
この定理の証明に関しては,以下の記事で紹介しています。
なお逆も成立します。具体的には,連続な関数 f がほとんどいたるところ微分可能でかつ任意の (a,b)\subset I に対して, f(b)-f(a)=\int_a^b f'(t)\, dt が成り立つなら f は絶対連続な関数になります。
4. 絶対連続関数の和・積も絶対連続
定理4(絶対連続関数の和・積も絶対連続)
f,g\colon [a,b]\to\R を絶対連続な関数とする。このとき, f+g, fg も絶対連続である。
証明は比較的簡単です。
略証
\|f\| =\sup_{x\in [a,b]} |f(x)| とする。有界閉区間上の連続関数は最大値・最小値を持つから, \|f\|, \|g\|<\infty である。
\small \begin{aligned}&|(f+g)(x_k)-(f+g)(x_{k-1})| \\ &\le |f(x_k)-f(x_{k-1})|+ |g(x_k)-g(x_{k-1})|, \\ &|(fg)(x_k)-(fg)(x_{k-1})| \\ &\le {\scriptsize|f(x_k)||g(x_k)-g(x_{k-1})|+|f(x_k)-f(x_{k-1})||g(x_{k-1})|} \\ &\le \|f\| |g(x_k)-g(x_{k-1})|+|f(x_k)-f(x_{k-1})|\|g\| \end{aligned}
であることから示せる。
略証終