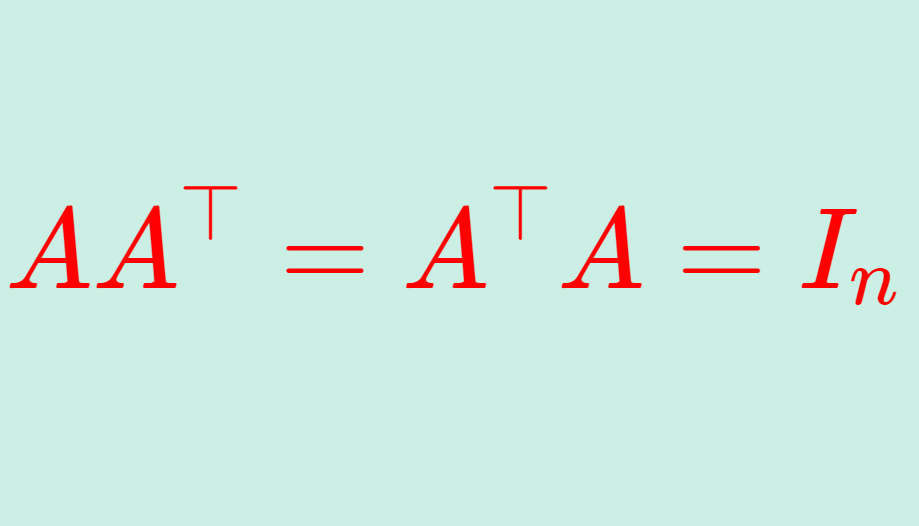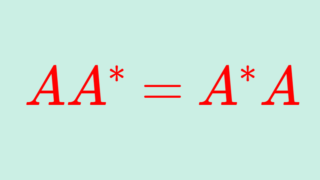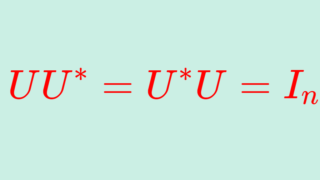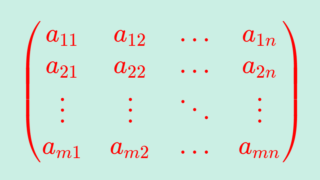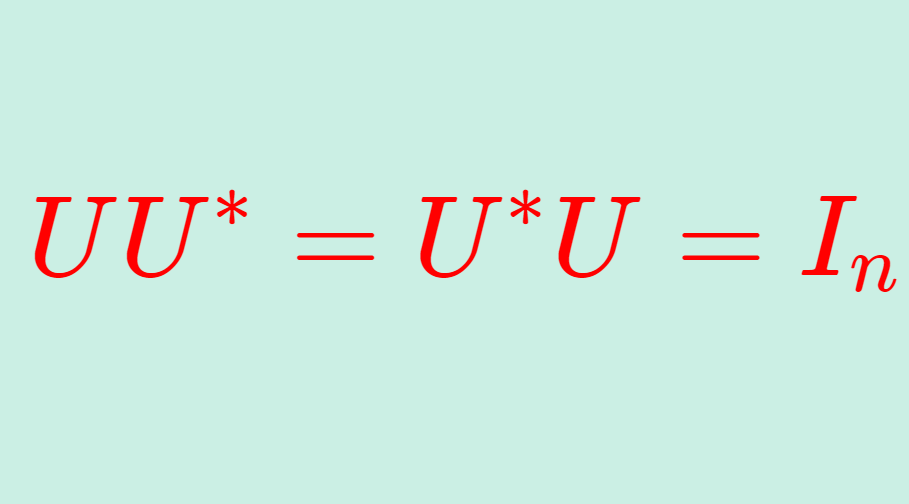直交行列とは, AA^\top =A^\top A = I_n となる正方行列 A を指します。これについて,定義と性質とその証明を行いましょう。
直交行列の定義
上の定義は, \color{red}A^{-1}=A^\top すなわち逆行列が転置行列になると言っても同じことです。これを定義にしても構いません。特に,直交行列は正則行列(可逆行列)です。
また,定義は AA^\top =I_n だけでも, A^\top A=I_n だけでも構いません。 これは,片方だけから, \det A\ne 0 が従う(→下の性質1.)ため,逆行列が存在することが分かり, AA^\top =I_n なら左から, A^\top A=I_n なら右から A^{-1} をかけることで, A^\top =A^{-1} が得られるためです。
直交行列の具体例
直交行列の具体例として,以下のようなものがあります。
直交行列の具体例
直交行列の性質10個
定理(直交行列の性質)
A,B を n 次直交行列とする。このとき,
1. \det A=\pm 1 (行列式)
2. AB も直交行列である。
3. A^{-1} も直交行列である。
4. A^\top も直交行列である。
さらに, A を 実行列(実直交行列)とし,\lVert \cdot \rVert, \langle \cdot, \cdot \rangle をそれぞれ実ベクトルのノルム・内積(後述)とすると,
5. A は対角化可能。
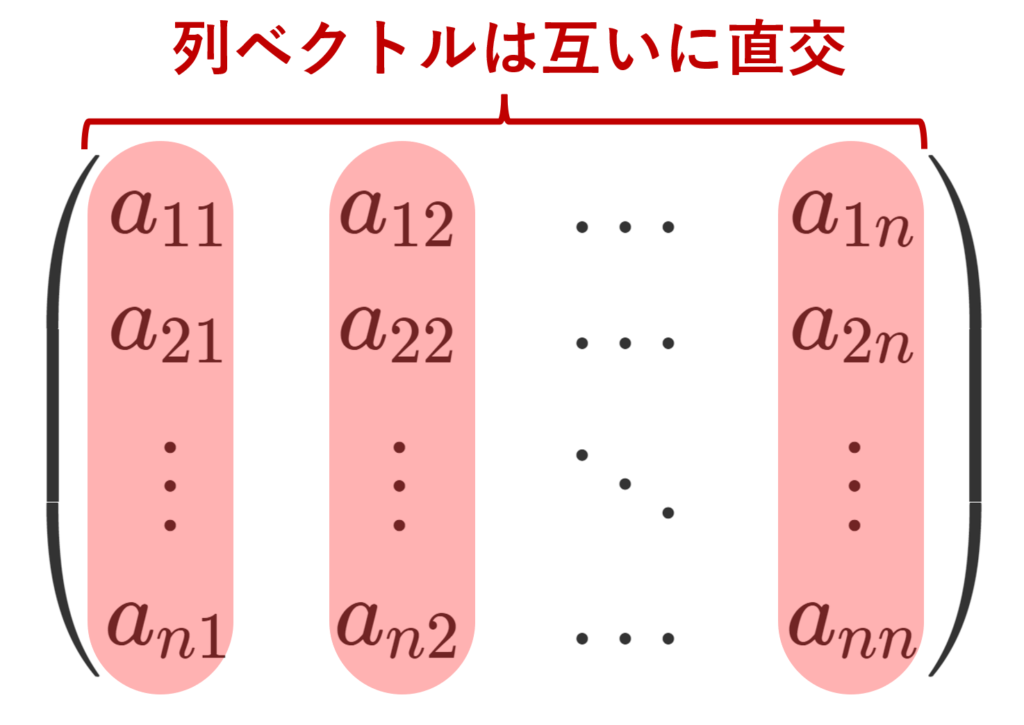
6. A の各列ベクトルは正規直交基底になっている。
7. A の各行ベクトルは正規直交基底になっている。
8. \lVert A\boldsymbol{x} \rVert= \lVert \boldsymbol{x} \rVert \quad(\boldsymbol{x}\in \mathbb{R}^n) ただし,\boldsymbol{x} は列ベクトルとする。(等長性)
9. \langle A\boldsymbol{x},A\boldsymbol{y}\rangle = \langle \boldsymbol{x}, \boldsymbol{y}\rangle\quad(\boldsymbol{x},\boldsymbol{y}\in \mathbb{R}^n) ただし,\boldsymbol{x},\boldsymbol{y} は列ベクトルとする。(内積を保つ)
10. A の全ての固有値 \lambda \in \mathbb{C} は |\lambda |=1 をみたす。
また,逆に6-9.のいずれかが成り立つとき,実行列 A は直交行列である。
A を「直交行列」という名前で呼ぶ理由の一つが6-7.ですね。
内積は \boldsymbol{x}=\begin{pmatrix} x_1\\ \vdots \\ x_n\end{pmatrix} , \boldsymbol{y} = \begin{pmatrix} y_1\\ \vdots \\ y_n \end{pmatrix} \in \mathbb{R}^n に対し,
\langle \boldsymbol{x},\boldsymbol{y}\rangle = \sum_{k=1}^n x_ky_k
と定義されます。また,
です(→数ベクトルの定義と数ベクトルにおけるノルム・内積)。これを踏まえて,1-10.を順番に証明していきましょう。
1. det A = ±1
証明
A,B を正方行列としたとき, \det AB = \det A \det B,\; \det A = \det A^\top であることに注意する(→行列式の性質6つの証明(列,行の線形性,置換,積,転置など))。
\det I_n = \det (AA^\top) = \det A \det A^\top = (\det A)^2
より, \det A = \pm1 である。
証明終
2. A,Bが直交行列⇒ABが直交行列
証明
A,B が正方行列のとき, (AB)^\top = B^\top A^\top であることに注意する(→転置行列の定義と基本的な性質11個の証明)。
\begin{aligned} AB(AB)^\top &= AB (B^\top A^\top) =A(BB^\top)A^\top\\&= AA^\top =I_n ,\\ (AB)^\top AB &= (B^\top A^\top)AB = B^\top(A^\top A) B\\ &= B^\top B = I_n \end{aligned}
であるから, AB は直交行列である。
証明終
3. 逆行列も直交行列
証明
一般に (A^{-1})^\top=(A^\top)^{-1} に注意する(→転置行列の定義と基本的な性質11個の証明)。
\begin{aligned}A^{-1} (A^{-1})^\top &= A^{-1} (A^\top)^{-1} =(A^\top A)^{-1} = I_n, \\ (A^{-1})^\top A^{-1}&= (A^\top)^{-1} A^{-1} =(AA^\top)^{-1}=I_n \end{aligned}
より, A^{-1} も直交行列である。
証明終
4. A^T も直交行列
これは (A^\top)^\top =A であることから明らかでしょう。 A^\top = A^{-1} なので,3.に帰着してもよいです。
5. 実直交行列は対角化可能
ここからは直交行列は実とします。
正規行列が対角化可能であることは以下で解説しています。
6-7. Aの各列ベクトル・行ベクトルは正規直交基底
証明
A = (\boldsymbol{x_1},\dots, \boldsymbol{x_n}) と列ベクトルに分解する。 すると,
A^\top A =\begin{pmatrix}\langle \boldsymbol{x_1},\boldsymbol{x_1}\rangle & \dots & \langle \boldsymbol{x_1},\boldsymbol{x_n}\rangle \\ \vdots & \ddots &\vdots \\ \langle \boldsymbol{x_n},\boldsymbol{x_1}\rangle &\dots & \langle \boldsymbol{x_n},\boldsymbol{x_n}\rangle \end{pmatrix}
であるから,\langle \boldsymbol{x_i},\boldsymbol{x_j}\rangle = \delta_{ij} となる(右辺はクロネッカーのデルタ)。従って, \boldsymbol{x_1},\dots, \boldsymbol{x_n} は正規直交基底である。
A= \begin{pmatrix} \boldsymbol{y_1}\\ \vdots \\ \boldsymbol{y_n}\end{pmatrix} と行ベクトルに分解する。すると,
AA^\top = \begin{pmatrix}\langle \boldsymbol{y_1},\boldsymbol{y_1}\rangle & \dots & \langle \boldsymbol{y_1},\boldsymbol{y_n}\rangle \\ \vdots & \ddots &\vdots \\ \langle \boldsymbol{y_n},\boldsymbol{y_1}\rangle &\dots & \langle \boldsymbol{y_n},\boldsymbol{y_n}\rangle \end{pmatrix}
であるから, \langle \boldsymbol{y_i},\boldsymbol{y_j}\rangle = \delta_{ij} となる(右辺はクロネッカーのデルタ)。従って, \boldsymbol{y_1},\dots, \boldsymbol{y_n} は正規直交基底である。
証明終
逆の証明
A の列ベクトルが正規直交基底ならば,上より A^\top A = I_n であり,直交行列になる。
A の行ベクトルが正規直交基底ならば,上より AA^\top =I_n であり,直交行列になる。
証明終
8-9. ||Ax|| = ||x||, <Ax, Ay> = <x, y>
8.が \lVert A\boldsymbol{x}\rVert = \lVert \boldsymbol{x}\rVert ,9.が \langle A\boldsymbol{x},A\boldsymbol{y}\rangle = \langle \boldsymbol{x}, \boldsymbol{y}\rangle です。
証明
一般に正方行列 A に対して, \langle A\boldsymbol{x},\boldsymbol{y}\rangle = \langle \boldsymbol{x}, A^\top \boldsymbol{y}\rangle が成り立つことに注意する(→転置行列の定義と基本的な性質11個の証明)。これより,
\langle A\boldsymbol{x}, A\boldsymbol{y} \rangle= \langle \boldsymbol{x}, A^\top A\boldsymbol{y} \rangle = \langle \boldsymbol{x}, \boldsymbol{y} \rangle
であるから,9.が示せた。これより,
となり,8.も示せた。
証明終
逆の証明
9.のとき,
\langle \boldsymbol{x}, \boldsymbol{y} \rangle =\langle A\boldsymbol{x}, A\boldsymbol{y} \rangle = \langle \boldsymbol{x}, A^\top A\boldsymbol{y} \rangle
が任意の列ベクトル \boldsymbol{x},\boldsymbol{y}\in\mathbb{R}^n で成立するので, A^\top A=I_n である。
8.のとき,polarization identity
\langle \boldsymbol{x}, \boldsymbol{y} \rangle =\frac{1}{4} ( \lVert \boldsymbol{x}+\boldsymbol{y}\rVert^2 - \lVert \boldsymbol{x}-\boldsymbol{y}\rVert^2)
を考えることで,9.が成立するため,上に帰着する。
証明終
10. 固有値をλとすると,|λ| = 1
8.で \lVert A\boldsymbol{x} \rVert = \lVert \boldsymbol{x}\rVert を証明しましたが,これは \boldsymbol{x} が複素ベクトル \boldsymbol{x}\in \mathbb{C}^n であっても成立します(このときノルムは \lVert\boldsymbol{x}\rVert = \sqrt{\sum_{k=1}^n |x_k|^2} です)。これを認めて,10.の証明をしましょう。
証明
\lambda \in\mathbb{C} を固有値, \boldsymbol{x}\in\mathbb{C}^n \setminus\{\boldsymbol{0}\} (列ベクトル)を固有ベクトルとする。すると, A\boldsymbol{x}=\lambda \boldsymbol{x} である。両辺ノルムを取ると
\lVert A\boldsymbol{x}\rVert = |\lambda| \lVert \boldsymbol{x}\rVert
である。一方で,8.より \lVert A\boldsymbol{x}\rVert = \lVert \boldsymbol{x}\rVert なので, \lVert \boldsymbol{x}\rVert = |\lambda| \lVert \boldsymbol{x}\rVert . したがって, |\lambda |=1 である。
証明終
無事に10個とも証明できましたね。
直交行列の複素数版
直交行列を複素数に拡張したものはユニタリ行列 (unitary matrix) といい,\color{red} UU^*=U^*U=I_n をみたすものとして定義されます。ただし, U^* = \overline{U}^\top は随伴行列(共役転置)です。これについては,以下で解説しています。