Webサイト「数学の景色」へようこそ!
本サイトでは,主に専門的な数学や,それに関連したテーマを概観します。
最近の記事

新着記事
カテゴリー別最新記事

微分積分学(大学)
【大学初等数学】微分積分学のオススメの本・参考書12選
2025.10.162025.12.26
ガウス積分のさまざまな形とその証明5つ
2021.10.122025.10.16
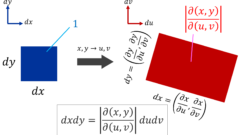
重積分の変数変換の方法とその例題~極座標変換の解説付き~
2021.10.112025.10.16
群・環・体
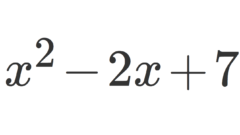
モニック多項式とは~定義・例・性質~
2023.05.042024.07.21
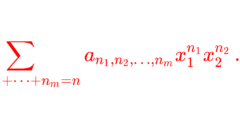
同次式(斉次式)とは
2023.03.062023.03.07
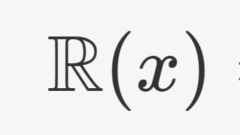
体の定義と具体例4つ
2022.06.132022.06.13
集合と位相

アレクサンドロフの1点コンパクト化を詳しく
2026.02.082026.02.13
【位相空間】nowhere dense(疎集合)とは
2026.01.302026.02.13
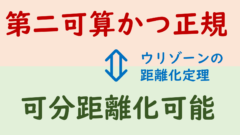
ウリゾーンの距離化定理とその証明
2026.01.23
確率論
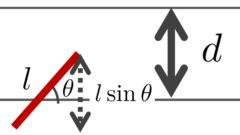
ビュフォンの針の理論
2023.01.252023.02.05
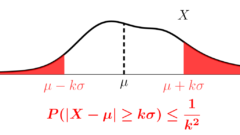
【確率論】チェビシェフの不等式とその例題・証明
2021.11.262024.01.03
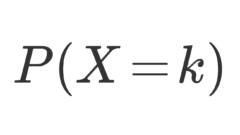
さまざまな確率分布まとめ
2021.08.032025.08.31
LaTeX
線形代数学
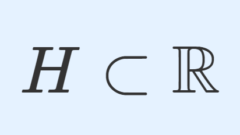
ハメル基底とは~有理数上実数の基底~
2022.07.192025.05.05
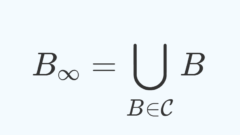
ベクトル空間には必ず基底が存在する証明~選択公理から~
2022.07.182026.01.24
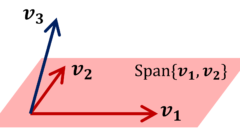
Spanの意味とは【線形結合】
2022.06.272024.10.15
数論

ピタゴラス数一覧【10000以下全て1593個】
2023.07.18
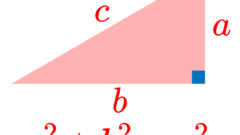
ピタゴラス数の求め方(解)・性質とその証明
2023.07.172023.07.18
【n!がpで割れる回数】ルジャンドルの定理とその証明
2022.06.092022.06.09
測度論
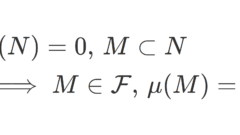
完備な測度と測度空間の完備化
2023.05.06
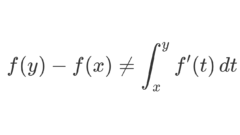
単調関数はほとんどいたるところ微分可能である証明
2023.04.162023.08.12
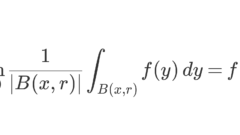
ルベーグの微分定理とその証明~測度の微分を添えて~
2023.04.102025.03.08
記号・記法
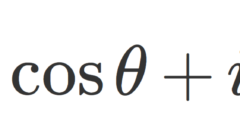
オイラーの公式・オイラーの等式とは~美しい等式の紹介~
2021.10.212022.08.01
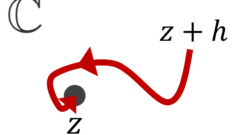
複素関数の微分~定義と例~
2021.10.202024.12.30
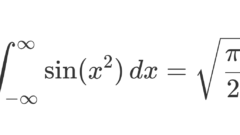
フレネル積分(sin(x^2)の積分)とその導出証明
2021.10.142024.07.17