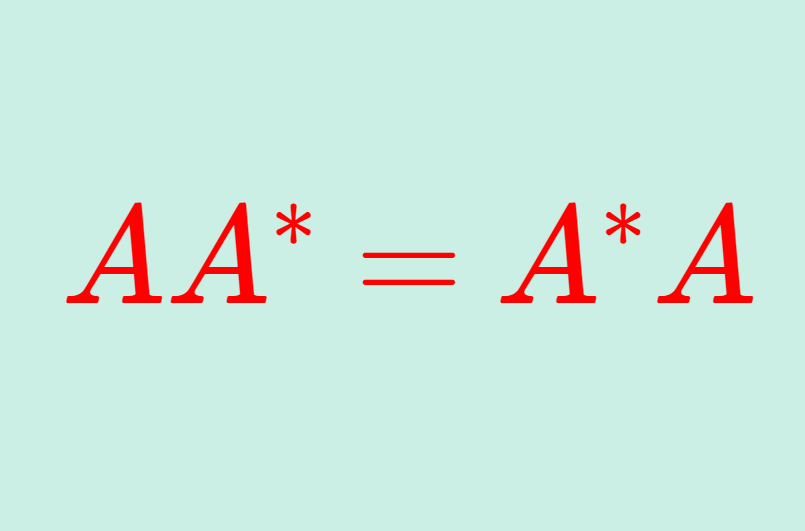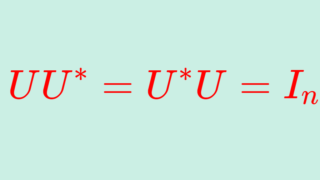正規行列とは, AA^* =A^*A が成り立つ正方行列を指します。ただし, A=\overline{A}^\top は A の随伴行列(共役転置)です。
これについて,その定義・具体例・性質を証明付きで紹介しましょう。
正規行列の定義
定義(正規行列)
n 次正方行列 A が正規行列 (normal matrix) であるとは,
\large\color{red} AA^* = A^* A
が成り立つことをいう。ただし,A^*=\overline{A}^\top は A の随伴行列(共役転置)を表す。
まずは,具体例を確認していきましょう。
正規行列の具体例
正規行列の具体例
一番最後の例は AA^*=A^*A= \begin{pmatrix} 2&1&1 \\ 1&2&1 \\ 1&1&2 \end{pmatrix} であり,その他のどの例にも当てはまりません。
正規行列の性質6つ
正規行列の性質について,
の6つを順番に紹介しましょう。
1. 正規行列が上三角行列ならば対角行列
証明
A=\begin{pmatrix} a_{11} &a_{12} & \dots & a_{1n} \\ & a_{22} & \dots & a_{2n} \\ && \ddots & \vdots \\ \Large{0} &&& a_{nn} \end{pmatrix}
とすると,
である。 A^* A=AA^* の (i,i) 成分を比較すると,
すなわち
したがって, a_{i\,i+1}= \dots = a_{in} =0 であり, A は対角行列である。
証明終
A が下三角行列のときも同様です。
2. 正規行列⇔||Ax|| = ||A^*x||
定理2(正規行列 \iff \lVert A\boldsymbol{x}\rVert = \lVert A^* \boldsymbol{x}\rVert)
正方行列 A が正規行列である必要十分条件は \lVert A\boldsymbol{x} \rVert = \lVert A^*\boldsymbol{x}\rVert\; (\boldsymbol{x}\in\mathbb{C}^n) が成り立つことである。
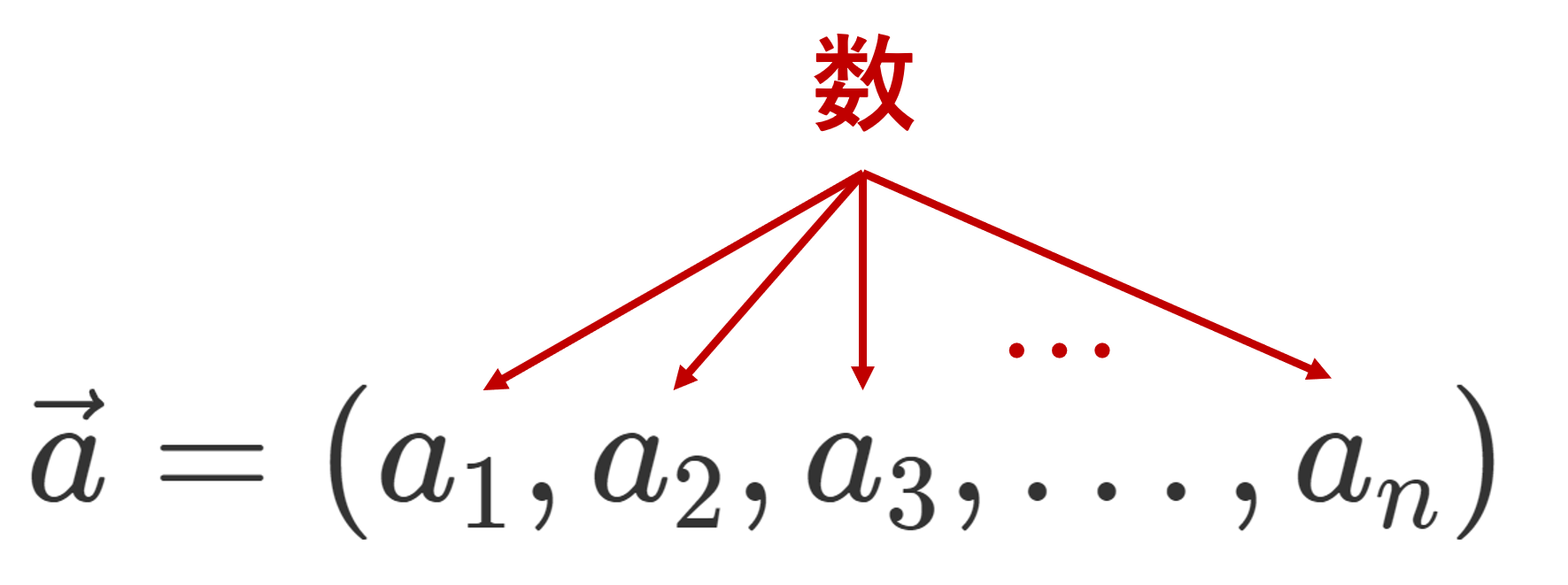
ここで, \boldsymbol{x} = \begin{pmatrix} x_1 \\ \vdots \\ x_n\end{pmatrix}, \boldsymbol{y} = \begin{pmatrix} y_1 \\ \vdots \\ y_n\end{pmatrix} \in \mathbb{C}^n に対して,
\begin{aligned}\lVert \boldsymbol{x}\rVert &= \sum_{k=1}^n |x_k|^2 = \sqrt{\langle \boldsymbol{x},\boldsymbol{x}\rangle}\\ \langle \boldsymbol{x},\boldsymbol{y} \rangle &= \sum_{k=1}^n x_k \overline{y}_k \end{aligned}
はそれぞれノルム・内積を表すことにします(→数ベクトルの定義と数ベクトルにおけるノルム・内積)。
証明
一般に A を正方行列とするとき, \langle A\boldsymbol{x},\boldsymbol{y} \rangle = \langle \boldsymbol{x},A^*\boldsymbol{y} \rangle であることに注意する(→随伴行列(エルミート転置,共役転置)の定義と性質10個)。
正規行列 \implies \lVert A\boldsymbol{x} \rVert = \lVert A^*\boldsymbol{x}\rVert について
A を正規行列とすると, \boldsymbol{x} \in\mathbb{C}^n に対し,
\begin{aligned}\lVert A\boldsymbol{x}\rVert^2 &= \langle A\boldsymbol{x},A\boldsymbol{x} \rangle = \langle \boldsymbol{x},A^* A\boldsymbol{x} \rangle \\ &= \langle \boldsymbol{x},A A^*\boldsymbol{x} \rangle = \langle A^* \boldsymbol{x},A^* \boldsymbol{x} \rangle \\ &= \lVert A^*\boldsymbol{x}\rVert^2. \end{aligned}
\lVert A\boldsymbol{x} \rVert = \lVert A^*\boldsymbol{x}\rVert \implies 正規行列について
仮定より,polarization identity
\begin{aligned}\langle \boldsymbol{x}, \boldsymbol{y} \rangle &=\frac{1}{4} ( \lVert \boldsymbol{x}+\boldsymbol{y}\rVert^2 - \lVert \boldsymbol{x}-\boldsymbol{y}\rVert^2 \\ &+i\lVert \boldsymbol{x}-i\boldsymbol{y}\rVert^2 -i\lVert \boldsymbol{x}+i\boldsymbol{y}\rVert^2 )\end{aligned}
によって, \langle A \boldsymbol{x}, A\boldsymbol{y} \rangle = \langle A^* \boldsymbol{x}, A^* \boldsymbol{y} \rangle が分かる。これを変形して
が任意の \boldsymbol{x},\boldsymbol{y}\in\mathbb{C}^n で成立するから, A^*A = AA^* でなければならない。
証明終
なお,後半の証明の途中で出てきましたが, \lVert A\boldsymbol{x} \rVert = \lVert A^*\boldsymbol{x}\rVert \iff \langle A \boldsymbol{x}, A\boldsymbol{y} \rangle = \langle A^* \boldsymbol{x}, A^* \boldsymbol{y} \rangle なので,特に A が正規 \iff \langle A \boldsymbol{x}, A\boldsymbol{y} \rangle = \langle A^* \boldsymbol{x}, A^* \boldsymbol{y} \rangle も分かります。
3. 正規行列⇔ユニタリ行列により対角化可能
定理3(正規行列 \iff ユニタリ行列により対角化可能)
n 次正方行列 A が正規行列である必要十分条件は, A がユニタリ行列により対角化できることである。
すなわちユニタリ行列 U が存在して,\color{red} U^{-1}AU は対角行列にできる( A は対角行列と相似である)。
ユニタリ行列とは,UU^* = U^*U=I_n が成り立つ行列です。ただし, A^* は A の随伴行列(共役転置)です。詳しくは,以下で解説しています。
なお,正規行列が対角化可能であることから,対角化可能の行列に成り立つすべての性質が成り立ちます。たとえば
ことが分かります。
証明には,正方行列 A,B に対し,(AB)^* = B^*A^* となることを用います(→随伴行列(エルミート転置,共役転置)の定義と性質10個)。
定理3の証明
ユニタリ行列により対角化可能 \implies 正規行列について
ユニタリ行列 U により, T=U^{-1}AU が対角行列になったとする。このとき, A=UTU^{-1} であり, U はユニタリ行列なので U^{-1} =U^* であるから, A=UTU^* となる。
T は対角行列より, TT^* = T^* T となることに注意して,
\begin{aligned}AA^* &= UTU^* ( UTU^* )^* = UT\textcolor{blue}{U^* U}T^* U^*\\ &= U\textcolor{red}{TT^*} U^*= U\textcolor{red}{T^*T}U^*\\&= UT^* \textcolor{blue}{U^*U} TU^* = (UTU^*)^* UTU^* \\&= A^*A \end{aligned}
となるから, A は正規行列である。
正規行列 \implies ユニタリ行列により対角化可能について
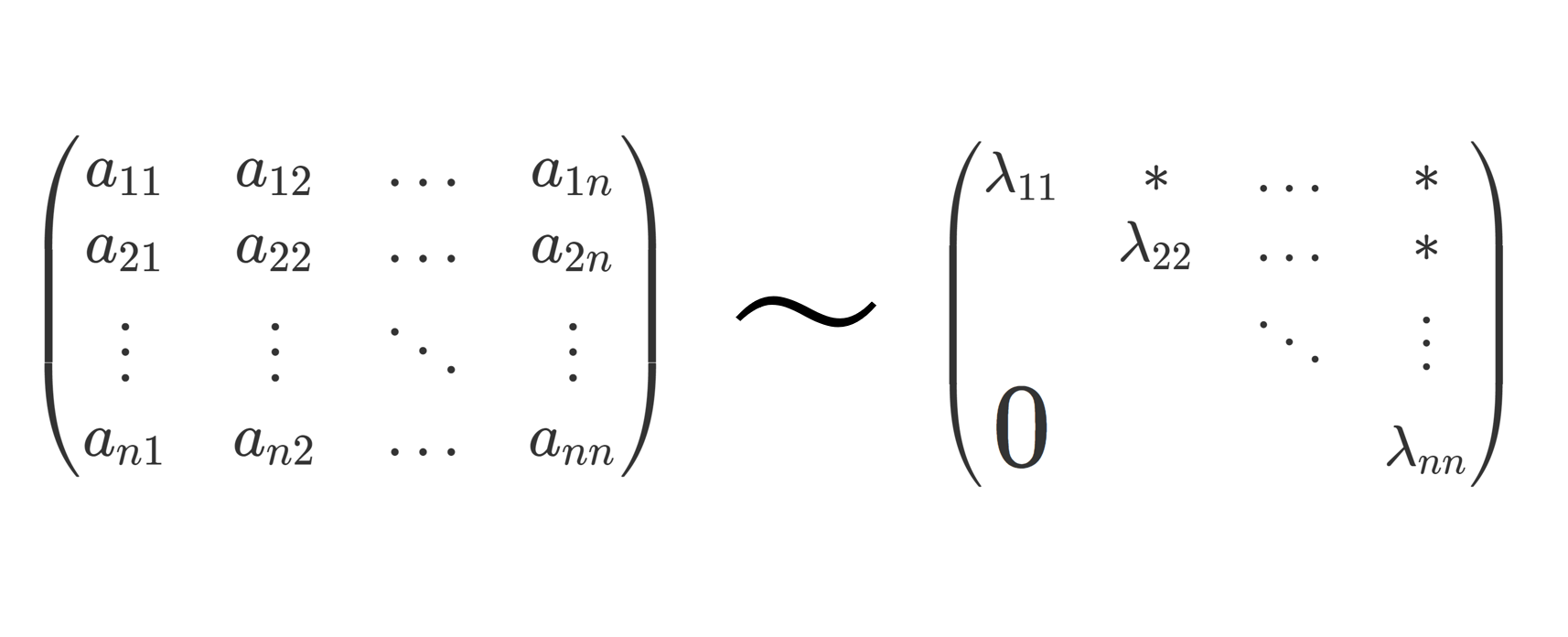
任意の正方行列はユニタリ行列により三角化可能であった。よって A を正規行列, U をユニタリ行列とし, T=U^{-1}AU= U^* AU が上三角行列であるとしてよい。このとき,
\begin{aligned} TT^* &= U^*AU(U^*AU)^* = U^* A\textcolor{blue}{UU^*}A^*U \\ &= U^* \textcolor{red}{AA^*} U = U^* \textcolor{red}{A^* A}U \\ &= U^*A^*\textcolor{blue}{UU^*}AU =(U^*AU)^* U^*AU \\ &= T^*T \end{aligned}
であるから,上三角行列 T は正規行列でもある。定理1より, T は対角行列となるから,題意は示された。
証明終
前半も後半もやっていることはほぼ同じですね。
なお,相似変換によって固有値は変化しませんから(→行列の相似とは~定義と性質6つの証明~),対角化後の対角成分には,正規行列 A の固有値が並びます(→対角行列の定義と基本的な性質6つ)この事実は以降で使います。
4. 正規行列の固有値が単位円上にあればユニタリ行列
定理4(正規行列の固有値が単位円上にあればユニタリ行列)
A を正規行列とする。 A の全ての固有値 \lambda が |\lambda|=1 をみたすとき, A はユニタリ行列である。すなわち,
\color{red}AA^* =A^*A = I_n
が成り立つ。ただし,I_n は n 次単位行列である。
定理3でも登場しましたが, A^* は A の随伴行列(共役転置)です。
証明
定理3より,正規行列 A をユニタリ行列 U により対角化して T=U^*AU を対角行列とする。この対角成分は A の固有値になるから,定理の仮定より, TT^* =T^*T = I_n が成り立つ。このとき, UU^* =U^*U=I_n も用いて
\begin{aligned} AA^* &= UTU^* (UTU^*)^* = UT\textcolor{blue}{U^*U}T^*U^*\\ &= U\textcolor{green}{TT^*} U^* = UU^* =I_n \end{aligned}
であり,同様に A^*A=I_n も分かるから, A はユニタリ行列である。
証明終
なお「ユニタリ行列 \implies 固有値は単位円上」も分かります(→ユニタリ行列の定義と性質10個とその証明)から, A を正規行列とするとき,
A はユニタリ行列 \iff A の固有値は単位円上
が成立します。また, A が実行列ならばユニタリ行列 \iff 直交行列なので, A を実正規行列とするとき,
A は直交行列 \iff A の固有値は単位円上
です。
5. 正規行列の固有値が実数ならばエルミート行列
定理5(正規行列の固有値が実数ならばエルミート行列)
A を正規行列とする。 A の全ての固有値 \lambda が \lambda \in\mathbb{R} をみたすとき, A はエルミート行列である。すなわち,
\color{red}A^* =A
が成り立つ。
証明
定理3より,正規行列 A をユニタリ行列 U により対角化して T=U^*AU を対角行列とする。この対角成分は A の固有値になるから,定理の仮定より, T^*=T が成り立つ。このとき,
A^* = (UTU^*)^* = UT^* U^* = UTU^* = A .証明終
なお「エルミート行列の固有値は実数」であることも分かりますから, A を正規行列とするとき,
A はエルミート行列 \iff A の固有値が実数
が成立します。また, A が実行列のときはエルミート行列 \iff 対称行列なので, A を実正規行列とするとき,
A は対称行列 \iff A の固有値が実数
が成り立ちます。
6. 正規行列の固有値が純虚数または0ならば歪エルミート行列
定理6(正規行列の固有値が実数ならばエルミート行列)
A を正規行列とする。 A の全ての固有値 \lambda が \lambda \in i\mathbb{R} をみたすとき, A は歪エルミート行列である。すなわち,
\color{red}A^* =-A
が成り立つ。
証明
定理3より,正規行列 A をユニタリ行列 U により対角化して T=U^*AU を対角行列とする。この対角成分は A の固有値になるから,定理の仮定より, T^*=-T が成り立つ。このとき,
A^* = (UTU^*)^* = UT^* U^* =- UTU^* = -A .証明終
なお「エルミート行列の固有値は純虚数または0」であることも分かりますから, A を正規行列とするとき,
A は歪エルミート行列 \iff A の固有値が純虚数または0
が成立します。また, A が実行列のときは歪エルミート行列 \iff 交代行列なので, A を実正規行列とするとき,
A は交代行列 \iff A の固有値が純虚数または0
が成り立ちます。